笔记Why BN works (MIT)
Paper地址:NIPS 2018 How Does Batch Normalization Help Optimization?
作者: Shibani Santurkar,Dimitris Tsipras, Andrew Ilyas, Aleksander Madry
解决了困扰挺久的BN问题,所以仔细读了这篇文章。理论是重头也不好编辑,啃了也不方便传…
博客迁移到:wonderseen.github.io
1. 主要内容
首先,关于BN为什么work,最广为流传的是:
- BN控制了输入层的分布(均值、方差)变化,成功地减少了internal covariate shift (ICS)
原文主要通过实验,证实了 输入层的分布稳定性对BN毫无帮助,真正产生效果的原因是:
- 优化平面变得更加光滑
- 光滑平面诱导了更稳定的梯度下降过程,有利于更快地训练
2. 前期实验
2.1 基础实验
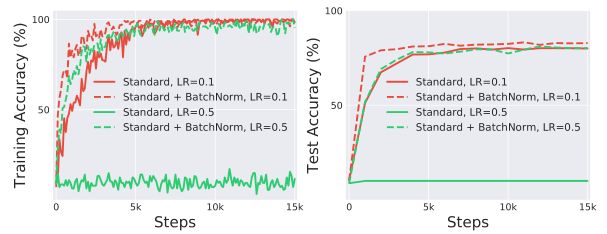
实验设计
用标准的VGG分别加BN和不加BN,在 CIFAR-10进行了实验,记录了训练准确率和测试准确率的变化曲线。注意:BN在非线性层之前进行,比如Relu。
实验结果
实验的Performance这个很明显,不多说。
2.2 ICS前期实验
实验设计
训练后,可视化随机的batch在输入层的分布。
实验结果分析
在输入层的分布稳定上,差异并不大。(意思可能是:虽然,主体的偏移和高密度区域一致,但是在低概率上分布还是有偏差的)。
2.3 实验拓展
由此提出两个问题:
- BN的有效性是否真的和ICS相关?
- BN所造成的层输入分布稳定性是否确实减少的ICS?
2.3.1 探究实验:BN之所以work是否和ICS有关
实验设计
- 对每个样本在BN层后,都加入
服从独立同分布的非0均值和非单位方差的随机噪声 - 并且每个step,注入的噪声属于不同的分布
- 加入噪声会产生ICS位移,这么做是为了使得每次激活都发生不同程度的偏差。
实验结果分析
上图记录了训练的每个step中,网络的指定层的均值和方差的单步变化值(时序上的差分)和与网络初始状态的差异值。
根据上图和下图右侧:注入噪声的网络,在后层的参数分布更不稳定。
然而,根据最终的训练准确度可以发现,带BN的网络中ICS的增加,并没有对模型的性能产生明显的影响,并且均高于不加BN层且不注入噪声的网络。除此之外,作者在不带BN情况下做同等的噪声注入,发现训练无法完成收敛。
因此,基于此实验证明:BN之所以有效,和ICS的控制关系不大。
2.3.2 探究实验: BN是否减少了ICS
由于BN实际是一种优化过程,所以,探讨网络层的ICS变化情况时候,更一般化地,我们是在探讨是参数怎么调节这个反应的。所以作者进行实验,更多地从优化底层关注梯度的情况,分析ICS在迭代过程中的变化情况。
于是,对ICS重新进行以下定义:
实验设计
- 训练了带BN和不带BN的网络
- 为了去除非线性特性和随机梯度的影响,还用full-batch梯度下降过程训练了25层的深度线性网络
实验结果分析
根据对BN的传统理解,BN会增加G和G‘的相关性,以此帮助减少ICS。(BN如何增加相关性?)
然而,训练过程中:
- 不加BN的标准网络几乎没有ICS
- BN的增加却增加了ICS,G和G’实际不相关
- 尤其在深度线性网络中尤其严重
- BN依然表现得很出色
因此,从优化角度入手,BN并没有减少ICS。
3. BN有效的真正原因
首先, BN最早的文章 给BN阐述了一系列其他的特性,包括:
- 避免梯度消失和梯度爆炸
- 对学习率或者初始解等超参数更加鲁棒
- 避免进入非线性激活函数的饱和区
- 等
但是都没有讲到BN优化问题的本质,本文作者对此进行了分析。
3.1 BN对损失过程的平滑
首先是BN保证了损失函数的Lipschitzness特性(如下)(怎么证明BN有的...?)
![]()
换句话说,就是保证了损失函数的梯度控制在很小的范围内,使得损失函数的单次迭代改变量较小,损失函数的突变相对少得多。根据损失过程,我们可以推测出带BN的网络,相比不带BN的网络,损失平面更平滑。
3.2 平滑作用的好处
这个平滑性质十分优秀,尤其在训练前期,把损失函数的梯度控制在更小的范围内,允许我们在前期训练过程中,更大范围内调节学习率,网络更容易收敛。
此外,作者在线性网络等网络,从余弦角度和平滑程度角度,对BN的平滑性质进行了测量,不赘述。
一点补充:
我记得,关于优化平面更平滑有助于训练的解释,17年已经有人做过相似的工作了。在清华的
why resnets work里有提到,该文中是用半凸性来(余弦角度)来说明平滑面的避免局部最优性质。
3.3 平滑优化平面的方法只有BN吗?
作者对输入层做中心化之前,进行L1、L2、L ∞ \infty ∞ 范数处理,对后期层进行相同的分布测量,发现不再具有高斯分布特点,已经无法保证对输入层分布的均值和方差的稳定性进行控制,甚至产生了更大ICS。但是,和BN相比,训练的性能相当,也有平滑优化平面的特性。L1甚至比BN效果更好。
4. 理论重头部分
慢慢啃。