数字图像处理-3.7混合空间增强法-骨骼图 基于opencv3.4.3的实现

引子

刚开始看冈萨雷斯的《数字图像处理》时，3.7节 混合空间增强法中图3.4.3中的全身骨骼图的印象非常深刻。牛XX啊，这么模糊，都能变得这么清楚。虽然书中也给出了大段大段的解释，但是能力实在有限，又是自学的，看得云里雾里，反正不明觉厉就是了。但是这个也一直留在脑中了，希望自己也能实现出来。

以下是纯参考书中的步骤，以及个人一些粗糙的理解，小试牛刀，欢迎大家拍砖以斧正。感谢~

【注】由于笔记本的屏幕不够大，所以截图没能截取完整，比如骨骼图中的脚就基本截断没有了。望见谅。

---

概述

先看看原图及一段细节图：
原图

截取原图的一段细节，并放大了看。

细节

由于是扫描图，可以看到骨骼周围有很多噪点，而骨骼本身以及红圈中的病变并不十分突出，看起来比较模糊。处理的目的是为了突出骨骼及病变部分。采用的是结合 拉普拉斯，均值模糊， sobel梯度，以及 图像的逻辑操作 。

最终效果对比：

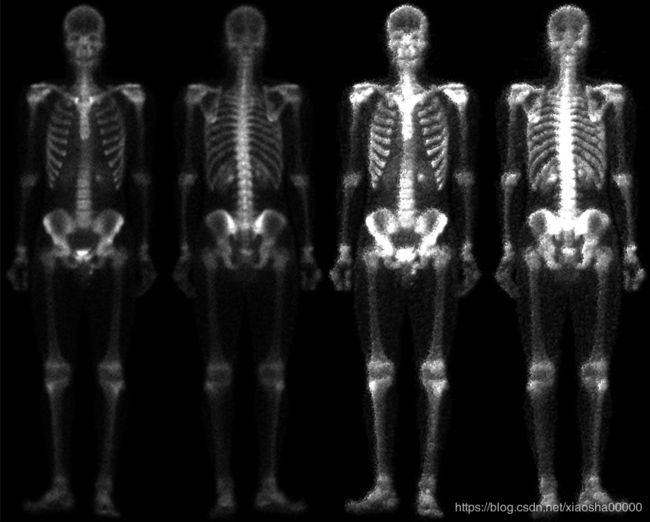
对于这个截图，我真是尽力了。o(╥﹏╥)o。屏幕太小了，如果做缩放，也会有损图像的质量。这个对比图是缩放之后的，将就看。有兴趣的，代码跑一遍，就很直观地看到对比效果啦。

---

步骤及效果分析

一、 先对原图做拉普拉斯处理，得图b，
拉普拉斯卷积核：3*3
-1，-1, -1
-1， 8，-1
-1，-1，-1
原图拉普拉斯之后，得图b。

【ps】:

1. 书中图b做了标定，即为了便于显示，则将灰度值为0的部分标定为127(大概)，这样看起来背景是灰色的。灰色背景相比黑色背景更能凸显出白色前景部分，更便于观察。
2. opencv中使用laplace卷积核做卷积操作，调用filter2D函数，想要得到灰色背景图，则需要将filter2D的第六个参数delta设置为127即可。
3. 这里没有直接使用opencv提供的Laplacian，而是调用filter2D接口。因为这里用到的卷积核与opencv中提供的Laplacian接口的卷积核不一致，所以需要自定义一个卷积核。

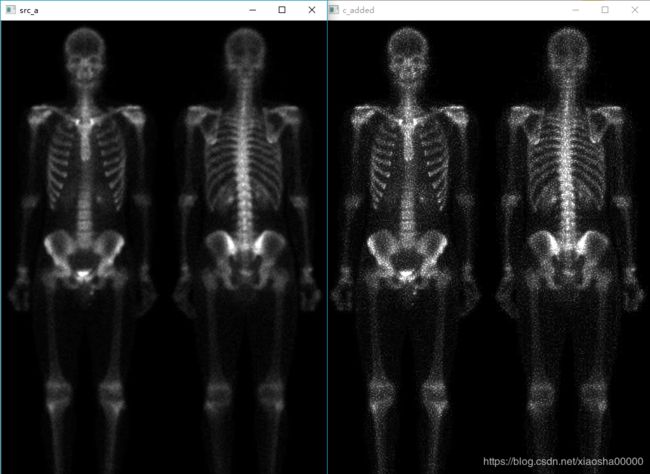
二、 拉普拉斯叠加到原图，得图c

左图是原图，右图是拉普拉斯叠加到原图的锐化图像。

将拉普拉斯结果叠加到原图，得到锐化后的图像。即在原图的基础上，突出的边缘。对比原图观察，可以看到，叠加锐化之后的图像，确实更突显了骨骼轮廓，但同时也骨骼周围的噪点也得到了放大，干扰仍然太多，效果不十分理想。

【ps】：

1. 上一步中，为了便于观察，突显拉普拉斯的效果，将背景标定为灰色。若想要得到图c的黑色背景，则需要将filter2D的第六个参数delta设置为0。

三、 将原图进行Sobel梯度处理，得图d

左图是图b拉普拉斯提取的边缘，右图原图的sobel梯度图d。
sobel卷积核：
x方向梯度
-1，-2, -1
0， 0， 0
1， 2， 1

y方向梯度
-1， 0, 1
-2， 0， 2
-1， 0， 1

sobel是一阶导数，laplace是二阶导数，但sobel会有个轻微的高斯模糊的效果，能少量的抑制噪点。对比可以看到，sobel虽然能抑制噪声，但是效果不好，骨骼周围仍存在大量噪点，并在sobel梯度的作用下放大了出来。

四、 对原图使用均值滤波后Sobel，得图e

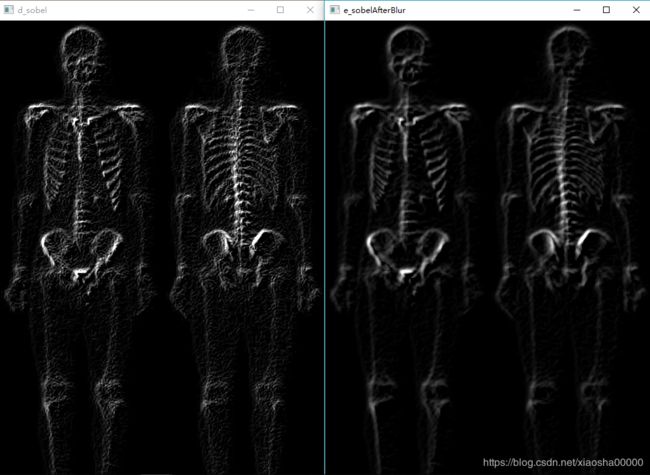
左图是图d直接对原图进行sobel梯度，右图是图e先平滑再sobel。
先采用5*5的均值滤波器，模糊图像，消除噪点，再用sobel梯度，获取模糊后的边缘。

对比观察，相比对原图直接sobel，用5*5均值模糊后，再sobel，骨骼周围的噪点明显少了不少，骨骼的大致轮廓也保留住了，但是骨骼的细节还是有所丢失。这个步骤，对于噪声的抑制起到了很好的作用。

五、 综合拉普拉斯和sobel的效果，得图f

左图是图b原图直接拉普拉斯提取边缘，中图是图d原图直接sobel，右图是图f原图先平滑再sobel，再与laplace效果合并得出的综合效果图。

对比观察，图f相比图b和图d，在5*5均值滤波的作用下不仅有效的抑制了骨骼周围的噪点，在sobel梯度的效果下，提取了主要的骨骼轮廓，在laplace的作用下，保留了骨骼的细节。

【ps】
这里，书中该步骤的原话是：由图c和图e相乘形成的掩蔽图像。
实际在opencv中把图c和图e做了一个与操作，提取了图c和图e的相同部分。我是这么理解的，以图e为mask，提取图c中的mask对应的部分，获取骨骼的轮廓细节。图c是拉普拉斯锐化后的效果，它增强了边缘细节，图c是滤除了骨骼周围噪点的大致骨骼框架，但图c丢失了骨骼的细节，综合两图，取两图的长处。从而获得了增强的骨骼框架，只要骨骼，不要噪点，或者尽可能少要噪点，这样的效果就比较理想了。
六、 图f叠加到原图，得g

左图是图a原图，中图是图c原图叠加laplace，右图是图g原图叠加混合增强。

对比观察，中图laplace锐化后的图像，虽然骨骼也增强了，但骨骼周围的噪点也放大了，干扰仍很多，右图是混合增强的效果，可以看出，骨骼被明显突出了很多，骨骼周围的噪点相比而言，看起来就不那么影响视觉了。

至此，就基本实现了混合增强。

七、对图g再微做调整，得图h

左图是图a原图，中图是图h

书中的最后一步是对图g采用了幂律变换，目的是为了增强图像。我这里是对图g做了个简单的自加，也是个增强，就没做幂律变换了。毕竟这个图的处理步骤的主要难点在于混合增强的理解。

对比观察，混合增强之后的最终效果图，相比原图a最终效果非常好，骨骼以及一些病变都有效的凸显出来，大致轮廓都存在，更便于图像的观察。

基于opencv3.4.3的具体代码如下：

    //卷积核：laplace锐化
	Mat kernel_laplace = (Mat_(3, 3) << -1, -1, -1, -1, 8, -1, -1, -1, -1);
	filter2D(src, laplace, CV_8U, kernel_laplace);
	imshow("b_laplace", laplace);

	//原图与laplace锐化结果相加得图c，突出边缘
	add(src, laplace, laplaceAddsrc);
	imshow("c_added", laplaceAddsrc);

	//计算原图的Sobel梯度，得图d
	Mat  sobel, gx, gy;
	Sobel(src, gx, CV_8U, 1, 0, 3, 1.0, 0.0, BORDER_DEFAULT);
	Sobel(src, gy, CV_8U, 0, 1, 3, 1.0, 0.0, BORDER_DEFAULT);
	convertScaleAbs(gx, gx);
	convertScaleAbs(gy, gy);
	add(gx, gy, sobel);
	convertScaleAbs(sobel, sobel);
	imshow("d_sobel", sobel);

	//5*5的均值滤波，模糊原图
	Mat blured, blur_sobel,multy;
	blur(src, blured, Size(5, 5), Point(-1, -1));
	Sobel(blured, gx, CV_8U, 1, 0, 3, 1.0, 0.0, BORDER_DEFAULT);
	Sobel(blured, gy, CV_8U, 0, 1, 3, 1.0, 0.0, BORDER_DEFAULT);
	convertScaleAbs(gx, gx);
	convertScaleAbs(gy, gy);
	add(gx, gy, blur_sobel);
	imshow("e_sobelAfterBlur", blur_sobel);

	//与操作
	Mat f, g;
	bitwise_and(laplaceAddsrc, blur_sobel, f);
	imshow("f", f);
	
	add(src, f, g);
	imshow("g", g);
	
	//效果图，自加一次，增强。冈萨雷斯里面是做幂律变换，我没做，只是做了个简单的增强，看着玩。
	add(g, g,g);
	imshow("h", g);

代码及原图下载链接如下：
https://download.csdn.net/download/xiaosha00000/10834295

【ps】

1. 若下载代码的话，记得改一下图片路径，我没做图片是否为空的判断，直接运行，图片路径不对的话，会报错的。
2. 由于图像中存在的概念和术语太多，自己也难免存在滥用的情况，若有使用不当，从而造成误解的地方，恳请大家指出。