用python完成《商务与经济统计(13版)》课后练习及案例分析——第2章和第3章
文章目录
- chapter2—40题
- chapter3—54题
- chapter3—60题
chapter2—40题
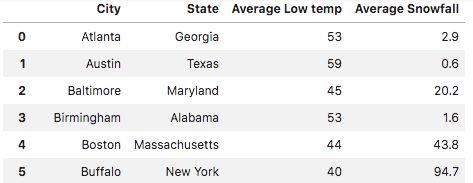
数据文件名为Sno.csv,包含美国51个主要城市1981~2010年的年平均最高气温和年平均降雪量
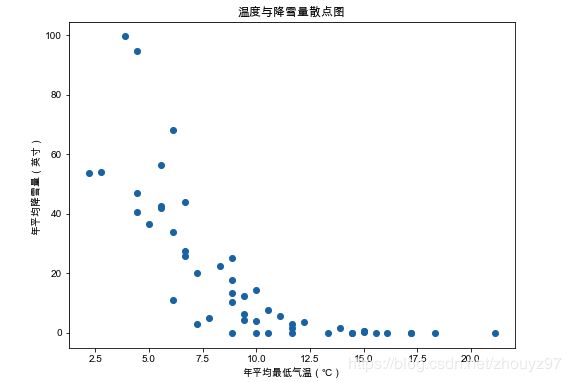
1.以年平均最低气温为横轴,年平均降雪量为数轴,绘制散点图
2.这两个变量之间存在相关关系吗
练习:
1.画散点图
#导入库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['Arial Unicode MS'] #用来正常显示中文标签(MAC)
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#读取数据
snow = pd.read_csv("/myfile/个人事务/数据分析学习/商务与经济统计/数据文件/第2章/Snow.csv",sep=",")
#画散点图
X = snow["Average Low temp"]
X = round((X-32)/1.8,2) #将温度单位转化为更熟悉的摄氏度,保留两位小数
Y = snow["Average Snowfall"]
fig = plt.figure(figsize=(8,6)) #设置图片尺寸
plt.scatter(X,Y)
plt.title("温度与降雪量散点图")
plt.xlabel("年平均最低气温(℃)")
plt.ylabel("年平均降雪量(英寸)")
2.年平均最低气温越低,年降雪量越高
chapter3—54题
BorderCrossings.csv文件,包含8月期间50个最繁忙的美国-加拿大和美国-墨西哥入境口岸的个人车辆过境数(四舍五入到最接近的1000辆)(美国交通运输局网站,2013年2月28日)
1.这些入境口岸过境次数的平均数和中位数是多少
2.第一四分位数和第三四分位数各为多少
3.用五数概括法汇总数据
4.数据是否包含异常值?绘制箱形图。
练习:
1.求平均数和中位数
BC = pd.read_csv("/myfile/个人事务/数据分析学习/商务与经济统计/数据文件/第3章/BorderCrossings.csv",sep=",")
BC.rename(columns={"Port Name":"Port_Name","Personal Vehicles (1000s)":"Personal_Vehicles"},inplace=True)
# 求平均数
BC.Personal_Vehicles.mean()
# 求中位数
BC.Personal_Vehicles.median()
2.求分位数
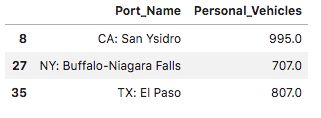
a.直接使用numpy库中的np.percentile()函数求分位数
q1 = np.percentile(BC["Personal_Vehicles"],25,interpolation="linear") #计算第一四分位数
q3 = np.percentile(BC["Personal_Vehicles"],75,interpolation="linear") #计算第三四分位数
print("第一四分位数是:{}".format(q1))
print("第三四分位数是:{}".format(q3))
![]()
查阅答案发现,计算结果和标准答案不同,因此根据书上公式自编一段函数求解
b.自编函数
先将样本排序, X = { x 1 , x 2 , … , x n } , x 1 < = x 2 < = . . . < = , x n X=\left\{x_{1},x_{2},…,x_{n} \right\},x_{1}<=x_{2}<=...<=,x_{n} X={x1,x2,…,xn},x1<=x2<=...<=,xn
根据书上公式,先求分位数的位置
L p = p 100 ∗ ( n + 1 ) L_{p} = \frac{p}{100}*(n+1) Lp=100p∗(n+1)
其中p为第p分位数,n为样本数量
若 L p L_{p} Lp为整数,则对应位置的值 x L p x_{L_{p}} xLp为第p分位数;若 L p L_{p} Lp不为整数,则记整数部分为 L p − i n t L_{p-int} Lp−int,小数部分为 L p − d e c L_{p-dec} Lp−dec,计算公式为
Q = x L p − i n t + ( x L p − i n t + 1 − x L p − i n t ) ∗ L p − d e c Q = x_{L_{p-int}} +(x_{L_{p-int}+1} -x_{L_{p-int}} )*L_{p-dec} Q=xLp−int+(xLp−int+1−xLp−int)∗Lp−dec
# 自定义函数
import math
def quantile(x,q):
x = sorted(x)
n = len(x)
local = q/100*(n+1) #计算分位数位置
local_dec,local_int = math.modf(local) #math的math.modf()函数,分别取浮点型数字的小数部分和整数部分
local_int = int(local_int) #转换数据类型
q_percent = x[local_int-1]+(x[local_int]-x[local_int-1])*local_dec #根据公式计算分位数的值
return q_percent
q_1 = quantile(BC["Personal_Vehicles"],25)
q_3 = quantile(BC["Personal_Vehicles"],75)
print("根据《商务与经济统计》定义得第一四分位数是:{}".format(q_1))
print("根据《商务与经济统计》定义得第三四分位数是:{}".format(q_3))
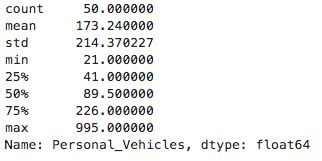
3.用五数概括法描述数据
五数指:最小值、第一四分位数、中位数、第三四分位数、最大值
# 五数概括法
BC.Personal_Vehicles.describe()
4.异常值检测,箱形图
根据书上的方法,数据的下限和上限为
下 限 = Q 1 − 1.5 ∗ I Q R 下限 = Q_{1} - 1.5*IQR 下限=Q1−1.5∗IQR
上 限 = Q 3 + 1.5 ∗ I Q R 上限 = Q_{3}+1.5*IQR 上限=Q3+1.5∗IQR
其中 I Q R = Q 3 − Q 1 IQR=Q_{3}-Q_{1} IQR=Q3−Q1
# 异常值检测
IQR = q3 - q1
lower = q1 - 1.5 * IQR
upper = q3 + 1.5 * IQR
BC["Personal_Vehicles"] = BC["Personal_Vehicles"].astype("float")
BC[((BC["Personal_Vehicles"] < lower) | (BC["Personal_Vehicles"] > upper))]
# 画箱形图
plt.boxplot(BC["Personal_Vehicles"])
chapter3—60题
罗素1000是包含美国最大的1000家公司的股票市场指数,以30家大公司的股票价格为依据。文件Russell.csv给出1988~2012年这些指数各自的年回报率
1.绘制这些回报率的散点图
2.计算每个指数的样本均值和样本标准差
3.计算样本相关系数
4.讨论这两个指数之间的相似性与不同性
练习:
1.散点图
# 读取文件
russ = pd.read_csv("/myfile/个人事务/数据分析学习/商务与经济统计/数据文件/第3章/Russell.csv",sep=",")
# 绘制散点图
y1 = russ["DJIA % Return"]
y2 = russ["Russell 1000 % Return"]
plt.scatter(y1,y2,c = "b",label = "DJIA")
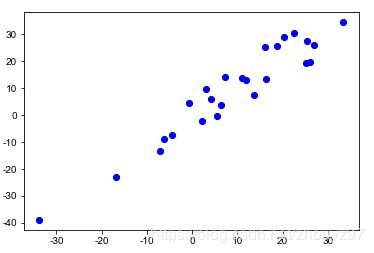
2.计算样本均值和样本标准差
样本均值: x ˉ = ∑ x i n \bar{x}=\frac{\sum x_{i}}{n} xˉ=n∑xi
样本标准差: s = ∑ ( x i − x ˉ ) 2 n − 1 s=\sqrt{\frac{\sum (x_{i}-\bar x)^2}{n-1}} s=n−1∑(xi−xˉ)2
# 计算样本均值和标准差
DJIA_mean = y1.mean()
DJIA_std = y1.std()
Russ_mean = y2.mean()
Russ_std = y2.std()
print("DJIA指数的样本均值为:{},样本方差为:{}".format(round(DJIA_mean,2),round(DJIA_std,2)))
print("Russell指数的样本均值为:{},样本方差为:{}".format(round(Russ_mean,2),round(Russ_std,2)))
# 计算样本相关系数
round(y1.corr(y2),4)
![]()
4.这两个指数呈正相关,Russell指数的样本标准差略大于DJIA指数。