中缀表达式、前缀表达式(波兰表达式)、后缀表达式(逆波兰表达式)算法分析与Java实现
在计算器中输入表达式,然后得出计算结果,是一个比较常见的过程,对于含有括号的运算表达式的运算顺序计算机需要自动识别,这里就涉及到表达式的转换。我们手写或者输入的都是中缀表达式,比如“1+(2-3)*45+41/(2*10)”,“1+(2-3)*45+41/2*10”。当然也可以支持其它函数表达式比如exp()等。
通常要转化为波兰表达式或者逆波兰表达式,方便计算机进行运算。也就是说第一步是中缀表达式转为(逆)波兰表达式,第二步计算逆波兰表达式。
以“1+(2-3)*45+41/2*10”为例进行算法说明。
中缀表达式转为前缀表达式对字符串进行逆向扫描,中缀表达式转为后缀表达式对字符串进行顺向扫描。
“1+(2-3)*45+41/(2*10)”
前缀:+ + 1 * - 2 3 45 / 41 * 2 10
后缀:1 2 3 - 45 * + 41 2 10 * / +
“1+(2-3)*45+41/2*10”
前缀:+ + 1 * - 2 3 45 / 41 * 2 10
后缀:+ + 1 * - 2 3 45 * / 41 2 10
中缀表达式转为前缀表达式
算法步骤:
初始化两个栈:运算符栈operators和操作数栈operands;
(2) 从右至左扫描中缀表达式;
(3) 遇到操作数时,将其压入operands;
(4) 遇到运算符时,比较其与operators栈顶运算符的优先级:
(4-1) 如果operators为空,或栈顶运算符为右括号“)”,则直接将此运算符入栈;
(4-2) 否则,若优先级比栈顶运算符的较高或相等,也将运算符压入operators;
(4-3)否则,将operators栈顶的运算符弹出并压入到operands中,再次转到(4-1)与operators中新的栈顶运算符相比较;
(5) 遇到括号时:
(5-1) 如果是右括号“)”,则直接压入operators;
(5-2) 如果是左括号“(”,则依次弹出operators栈顶的运算符,并压入operands,直到遇到右括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最左边;
(7) 将operators中剩余的运算符依次弹出并压入operands;
(8) 依次弹出operands中的元素并输出,结果即为中缀表达式对应的前缀表达式。
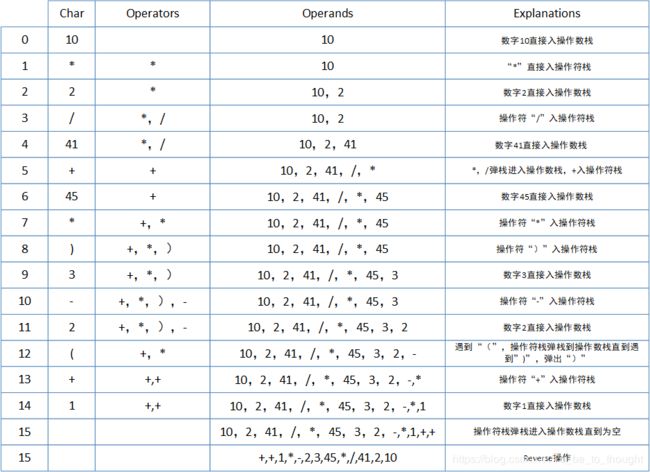
具体过程如下:
中缀表达式转为后缀表达式
算法步骤:
与转换为前缀表达式相似,遵循以下步骤:
(1) 初始化两个栈:操作符栈operators和操作数栈operands;
(2) 从左至右扫描中缀表达式;
(3) 遇到操作数时,将其压入operands;
(4) 遇到运算符时,比较其与operators栈顶运算符的优先级:
(4-1) 如果operators为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
(4-2) 否则,若优先级比栈顶运算符的高,也将运算符压入operators(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
(4-3) 否则,将operators栈顶的运算符弹出并压入到operands中,再次转到(4-1)与S1中新的栈顶运算符相比较;
(5) 遇到括号时:
(5-1) 如果是左括号“(”,则直接压入operators;
(5-2) 如果是右括号“)”,则依次弹出operators栈顶的运算符,并压入operands,直到遇到左括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最右边;
(7) 将S1中剩余的运算符依次弹出并压入operands;
具体步骤如下:
Java实现
具体实现采用的双端队列替代栈,因为涉及到逆序问题使用起来更加方便。目前只支持整型数计算
import java.util.Deque;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Stack;
public class Parser {
public static HashMap priority;
public Parser()
{
priority = new HashMap<>(); //存储运算符优先级,越大优先级越高
priority.put("+", 2);
priority.put("-", 2);
priority.put("*", 3);
priority.put("/", 3);
}
public static String[] postfixExpression(String s) {
Deque operands = new LinkedList<>();
Deque operators = new LinkedList<>();
for (int i = 0; i < s.length(); i++) {
//遇到数字字符,尝试往后读取整个数字
if (s.charAt(i) >= '0' && s.charAt(i) <= '9') {
int j = i, num = s.charAt(i) - '0';
while (j + 1 < s.length() && s.charAt(j + 1) >= '0' && s.charAt(j + 1) <= '9') {
j++;
num = num * 10 + s.charAt(j) - '0';
}
operands.add(String.valueOf(num));
i = j;
} else if (priority.containsKey(String.valueOf(s.charAt(i)))) { //遇到运算符
String op = String.valueOf(s.charAt(i));
//当前运算符优先级比运算符栈栈顶优先级高或者相等 或者栈顶为括号
if (operators.isEmpty() || operators.peekLast().equals("(") || priority.get(op) > priority.get(operators.peekLast()))
operators.add(op);
else {
while (!operators.isEmpty() && priority.get(operators.peekLast()) >= priority.get(op)) {
operands.add(operators.pollLast());
}
operators.add(op);
}
} else if (s.charAt(i) == '(')
operators.add("(");
else if (s.charAt(i) == ')') {
while (!operators.isEmpty() && !operators.peekLast().equals("("))
operands.add(operators.pollLast());
if (!operators.isEmpty())
operators.pollLast();
}
}
while (!operators.isEmpty()) {
operands.add(operators.pollLast());
}
String[] ans = new String[operands.size()];
int i = 0;
while (!operands.isEmpty())
ans[i++] = operands.pollFirst();
return ans;
}
public static String[] prefixExpression(String s) {
Deque operands = new LinkedList<>();
Deque operators = new LinkedList<>();
for (int i = s.length() - 1; i >= 0; i--) {
//遇到数字字符,尝试往后读取整个数字
if (s.charAt(i) >= '0' && s.charAt(i) <= '9') {
int j = i, num = s.charAt(i) - '0', count = 10;
while (j - 1 >= 0 && s.charAt(j - 1) >= '0' && s.charAt(j - 1) <= '9') {
j--;
num = num + count * (s.charAt(j) - '0');
count *= 10;
}
operands.add(String.valueOf(num));
i = j;
} else if (priority.containsKey(String.valueOf(s.charAt(i)))) { //遇到运算符
String op = String.valueOf(s.charAt(i));
//当前运算符优先级比运算符栈栈顶优先级高或者相等 或者栈顶为括号
if (operators.isEmpty() || operators.peekLast().equals(")") || priority.get(op) >= priority.get(operators.peekLast()))
operators.add(op);
else {
while (!operators.isEmpty() && priority.get(operators.peekLast()) > priority.get(op)) {
operands.add(operators.pollLast());
}
operators.add(op);
}
} else if (s.charAt(i) == '(') {
while (!operators.isEmpty() && !operators.peekLast().equals(")"))
operands.add(operators.pollLast());
operators.pollLast();
} else if (s.charAt(i) == ')')
operators.add(")");
}
while (!operators.isEmpty()) {
operands.add(operators.pollLast());
}
String[] ans = new String[operands.size()];
int i = 0;
while (!operands.isEmpty())
ans[i++] = operands.pollLast();
return ans;
}
public static void main(String[] args) {
Parser p = new Parser();
String s1 = "1+(2-3)*45+41/(2*10)"; // 1 2 3 - 45 * +41 2 / +
String s2="1+(2-3)*45+41/2*10";
String[] ans = p.prefixExpression(s1);
System.out.println(calculateByPrefix(ans));
}
}
得到前缀或者后缀表达式之后计算比较方便,借助一个栈即可,代码如下:
//根据后缀表达式计算值
public static int calculateByPostfix(String[] tokens) {
Stack stack = new Stack();
for (String s : tokens) {
if (s.length() == 1) {
char ch = s.charAt(0);
switch (ch) {
case '+': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(a + b));
break;
}
case '-': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(b - a));
break;
}
case '*': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(a * b));
break;
}
case '/': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(b / a));
break;
}
default:
stack.push(s);
}
} else
stack.push(s);
}
return Integer.valueOf(stack.pop());
}
//根据前缀表达式计算值
public static int calculateByPrefix(String[] tokens) {
Stack stack = new Stack<>();
for (int i = tokens.length - 1; i >= 0; i--) {
String s = tokens[i];
if (s.length() == 1) {
char ch = s.charAt(0);
switch (ch) {
case '+': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(a + b));
break;
}
case '-': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(a - b));
break;
}
case '*': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(a * b));
break;
}
case '/': {
int a = Integer.valueOf(stack.pop());
int b = Integer.valueOf(stack.pop());
stack.push(String.valueOf(a / b));
break;
}
default:
stack.push(s);
}
} else
stack.push(s);
}
return Integer.valueOf(stack.pop());
} 测试代码:
public static void main(String[] args) {
Parser p = new Parser();
String s1 = "1+(2-3)*45+41/(2*10)"; // 1 2 3 - 45 * +41 2 / +
String s2 = "1+(2-3)*45+41/2*10";
String[] ansPre1 = p.prefixExpression(s1);
String[] ansPost1=p.postfixExpression(s1);
String[] ansPre2 = p.prefixExpression(s2);
String[] ansPost2=p.postfixExpression(s2);
println(ansPre1);
println(ansPost1);
println(ansPre1);
println(ansPre2);
System.out.println(calculateByPrefix(ansPre1));
System.out.println(calculateByPostfix(ansPost1));
System.out.println(calculateByPrefix(ansPre2));
System.out.println(calculateByPostfix(ansPost2));
}结果:
+ + 1 * - 2 3 45 / 41 * 2 10
1 2 3 - 45 * + 41 2 10 * / +
+ + 1 * - 2 3 45 / 41 * 2 10
+ + 1 * - 2 3 45 * / 41 2 10
-42
-42
156
156
算法题链接
上述算法主要是对字符串的一些处理技巧和经验。基本使用for循环代替while,另外涉及到字符串前后关系的处理一般会使用栈这个数据结构。
LeetCode--224. Basic Calculator
class Solution {
public int calculate(String s) {
Stack stack=new Stack<>();
int sign=1,res=0;int num=0;
for(int i=0;i LeetCode--227. Basic Calculator II
class Solution {
public int calculate(String s) {
int num=0;
char sign='+';
Stack stack=new Stack<>();
for(int i=0;i LeetCode--282. Expression Add Operators
class Solution {
public static List ret;
public List addOperators(String num, int target) {
ret=new LinkedList<>();
backtrace(num,new StringBuilder(),target,0,0,0);
return ret;
}
public static void backtrace(String num,StringBuilder sb,int target,int start,long pre,long sum){
if(start==num.length())
{
if(sum==target)
ret.add(sb.toString());
return;
}
for(int i=start;istart)
break;
long val=Long.valueOf(num.substring(start,i+1));
int len=sb.length();
if(start==0){
backtrace(num,sb.append(val),target,i+1,val,sum+val);
sb.setLength(len);
}else{
backtrace(num,sb.append('+').append(val),target,i+1,val,sum+val);
sb.setLength(len);
backtrace(num,sb.append('-').append(val),target,i+1,-val,sum-val);
sb.setLength(len);
backtrace(num,sb.append('*').append(val),target,i+1,pre*val,sum-pre+pre*val);
sb.setLength(len);
}
}
}
} LeetCode--150. Evaluate Reverse Polish Notation
class Solution {
public int evalRPN(String[] tokens) {
Stack stack=new Stack();
for(String s:tokens)
{
if(s.length()==1)
{
char ch=s.charAt(0);
switch(ch)
{
case '+':
{
int a=Integer.valueOf(stack.pop());
int b=Integer.valueOf(stack.pop());
stack.push(String.valueOf(a+b));
break;
}
case '-':
{
int a=Integer.valueOf(stack.pop());
int b=Integer.valueOf(stack.pop());
stack.push(String.valueOf(b-a));
break;
}
case '*':
{
int a=Integer.valueOf(stack.pop());
int b=Integer.valueOf(stack.pop());
stack.push(String.valueOf(a*b));
break;
}
case '/':
{
int a=Integer.valueOf(stack.pop());
int b=Integer.valueOf(stack.pop());
stack.push(String.valueOf(b/a));
break;
}
default:
stack.push(s);
}
}
else
stack.push(s);
}
return Integer.valueOf(stack.pop());
}
} LeetCode--394. Decode String
class Solution {
public String decodeString(String s) {
int i=0;
Stack stack=new Stack<>();
while(i='0' && stack.peek()<='9')
{
frequency=pos*(stack.pop()-'0')+frequency;
pos*=10;
}
for(int j=0;j=0;k--)
stack.push(tsb.charAt(k));
}
}
i++;
}
char[] ret=new char[stack.size()];
for(int m=stack.size()-1;m>=0;m--)
ret[m]=stack.pop();
return new String(ret);
}
} 参考:
https://zh.wikipedia.org/wiki/%E6%B3%A2%E5%85%B0%E8%A1%A8%E7%A4%BA%E6%B3%95
https://blog.csdn.net/Antineutrino/article/details/6763722