两连杆机器鱼的简单建模以及MATLAB仿真
两连杆机器鱼的简单建模方法
在机器鱼的建模过程中,无可避免地会遇到一个问题,那就是:
机器鱼的推进力是如何产生的呢?
如果不想明白这个问题,我们没有对推力建模,机器鱼甚至都无法前进,这样我们的建模工作自然就无法往下进行了。
如何对这个问题的解答呢?
生物学家会认为鱼类会利用身体摆动产生反卡门涡街,向后喷射,从而获得推进力,但貌似具体的建模方法有些复杂。
一些文献中,把鱼尾巴当做是一个机翼,用翼型理论来分析鱼尾受力,这样确实是一种方法。
一些文献中,则利用细长体理论来建模鱼尾受力。(这个不太清楚,就不瞎说了>_<)
以上方法,我都可以理解推力是如何产生的,但是最让我郁闷的就是:
一些文献中把鱼尾巴的力分作两部分,一是附加质量力,二是粘滞阻力。
我非常不能理解,如果只有这两部分力的话,真的还可以创造向前的力吗?
毕竟咋一看,附加质量就是在原来基础上增加了一些质量,并不会产生推力,而阻力感觉上也不可能会产生推力。
(附加质量实际上就是说在水里物体运动要带动周围流体一块运动,这种效应可以近似看做为本体的质量增加了,增加的这部分质量就是附加质量。)
那么这样子是否真的可以产生推力呢?
直觉不可靠,让我们从一个简单的两连杆机器鱼出发,对其建立模型,来揭开我们的谜底吧!
1 两连杆机器鱼示意图
说明:
点 b b b代表鱼头质心,同时也是转动关节的所在位置,而点 t t t则代表鱼尾质心,从鱼头质心到鱼尾质心的向量由 r b t r_{bt} rbt表示,鱼尾的转动角用 θ \theta θ表示。图中的坐标系为鱼头坐标系。
1.1 关节运动规律
假设鱼尾以某种运动规律进行运动,具体而言就是, θ \theta θ的变化遵循某种规律,这里采用的是余弦函数,如下:
θ = b cos ( a t ) θ ˙ = − a b sin ( a t ) θ ¨ = − a 2 b cos ( a t ) \begin{aligned} \theta &= b\cos(at)\\ \dot{\theta} &= -ab\sin(at)\\ \ddot{\theta} &= -a^2b\cos(at)\\ \end{aligned} θθ˙θ¨=bcos(at)=−absin(at)=−a2bcos(at)
2 两连杆机器鱼建模过程
2.1 鱼头分析
(1)位置和速度更新
假设鱼头在世界系的位置为 P w P_w Pw,姿态为 γ \gamma γ,这里就考虑二维的,所以姿态可以就用一个偏航角表达。
假设鱼头的速度为 V b V_b Vb,角速度为 Ω b \Omega_b Ωb,代表的是鱼头相对于惯性系的速度在鱼头坐标系的表示。
(注意,这里 P b P_b Pb, V b V_b Vb, Ω b \Omega_b Ωb表示的还是三维向量)
位置更新公式为:
P w = ∫ w R b V b d t P_w=\int {\vphantom{}}^{w}R_b V_b \ dt Pw=∫wRbVb dt
γ = ∫ ( w R b Ω b ) z d t \gamma = \int ({\vphantom{}}^{w}R_b\Omega_b)_z \ dt γ=∫(wRbΩb)z dt
这里的 ( ∗ ) z (*)_z (∗)z代表的就是括号内向量的第三个的元素。
另外:
w R b = [ cos γ − sin γ 0 sin γ cos γ 0 0 0 1 ] {\vphantom{}}^{w}R_b= \left[ \begin{matrix} \cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{matrix} \right] wRb=⎣⎡cosγsinγ0−sinγcosγ0001⎦⎤
速度更新公式为:
V b = ∫ V ˙ b d t V_b=\int \dot{V}_b \ dt Vb=∫V˙b dt
Ω b = ∫ Ω ˙ b d t \Omega_b=\int \dot{\Omega}_b \ dt Ωb=∫Ω˙b dt
(2)水动力分析
在文章开头说了,我们主要是为了验证如果只考虑附加质量力和粘滞阻力的话,是否能产生推进力。附加质量实际上就是质量,我们只需要在正常的质量上再设置大一些就可以了,这里不需要再分析。而粘滞阻力,我们采取如下建模方式:
F d r a g = − 1 2 [ c 1 ⋅ s i g n ( V b , x ) ∣ ∣ V b , x ∣ ∣ 2 c 2 ⋅ s i g n ( V b , y ) ∣ ∣ V b , y ∣ ∣ 2 c 3 ⋅ s i g n ( V b , z ) ∣ ∣ V b , z ∣ ∣ 2 ] F_{drag} = -\frac{1}{2} \left[ \begin{matrix} c_1\cdot sign(V_{b,x})||V_{b,x}||^2\\ c_2\cdot sign(V_{b,y})||V_{b,y}||^2\\ c_3\cdot sign(V_{b,z})||V_{b,z}||^2\\ \end{matrix} \right] Fdrag=−21⎣⎡c1⋅sign(Vb,x)∣∣Vb,x∣∣2c2⋅sign(Vb,y)∣∣Vb,y∣∣2c3⋅sign(Vb,z)∣∣Vb,z∣∣2⎦⎤
M d r a g = − 1 2 [ c 4 ⋅ s i g n ( Ω b , x ) ∣ ∣ Ω b , x ∣ ∣ 2 c 5 ⋅ s i g n ( Ω b , y ) ∣ ∣ Ω b , y ∣ ∣ 2 c 6 ⋅ s i g n ( Ω b , z ) ∣ ∣ Ω b , z ∣ ∣ 2 ] M_{drag} = -\frac{1}{2} \left[ \begin{matrix} c_4\cdot sign(\Omega_{b,x})||\Omega_{b,x}||^2\\ c_5\cdot sign(\Omega_{b,y})||\Omega_{b,y}||^2\\ c_6\cdot sign(\Omega_{b,z})||\Omega_{b,z}||^2\\ \end{matrix} \right] Mdrag=−21⎣⎡c4⋅sign(Ωb,x)∣∣Ωb,x∣∣2c5⋅sign(Ωb,y)∣∣Ωb,y∣∣2c6⋅sign(Ωb,z)∣∣Ωb,z∣∣2⎦⎤
其中 s i g n ( ∗ ) sign(*) sign(∗)代表符号函数。
(3)受力分析
假设鱼头受到来自鱼尾的力 F F F以及力矩 M M M,利用牛顿欧拉公式,则有:
F + F d r a g = m b V ˙ b + m b Ω b × V b M + M d r a g = J b Ω ˙ b + Ω b × J b Ω b \begin{aligned} F+F_{drag}&=m_b\dot{V}_b+m_b\Omega_b\times V_b\\ M+M_{drag}&= J_b\dot{\Omega}_b + \Omega_b\times J_b\Omega_b \end{aligned} F+FdragM+Mdrag=mbV˙b+mbΩb×Vb=JbΩ˙b+Ωb×JbΩb
其中, m b m_b mb和 J b J_b Jb分别是鱼头的质量和转动惯量 。
所以,鱼头的加速度和角加速度为:
V ˙ b = ( F + F d r a g − m b Ω b × V b ) / m b Ω ˙ b = ( M + M d r a g − Ω b × J b Ω b ) / J b (1) \begin{aligned} \dot{V}_b &= (F+F_{drag}-m_b\Omega_b\times V_b)/m_b\\ \dot{\Omega}_b& = (M+M_{drag}-\Omega_b\times J_b\Omega_b)/J_b\\ \end{aligned} \tag{1} V˙bΩ˙b=(F+Fdrag−mbΩb×Vb)/mb=(M+Mdrag−Ωb×JbΩb)/Jb(1)
2.2 鱼尾分析
(1)鱼尾速度计算
首先,根据图片,我们可以知道 r b t r_{bt} rbt的表达式如下
r b t = [ r ⋅ cos θ r ⋅ sin θ 0 ] r_{bt}= \left[ \begin{matrix} r\cdot\cos\theta\\ r\cdot\sin\theta\\ 0 \end{matrix} \right] rbt=⎣⎡r⋅cosθr⋅sinθ0⎦⎤
其中, r r r代表了从 b b b点到 t t t点的距离。
其次,我们计算鱼尾的速度和加速度,如下:
V t = V b + ( Ω b + θ ˙ e 3 ) × r b t Ω t = Ω b + θ ˙ e 3 V ˙ t = V ˙ b + Ω t × V b + Ω ˙ t × r b t + Ω t × Ω t × r b t Ω ˙ t = Ω ˙ b + θ ¨ e 3 \begin{aligned} V_t &= V_b + (\Omega_b+\dot{\theta}\mathbf{e}_3)\times r_{bt}\\ \Omega_t &= \Omega_b+\dot{\theta}\mathbf{e}_3\\ \dot{V}_t &= \dot{V}_b + \Omega_t\times V_b+\dot{\Omega}_t\times r_{bt}+\Omega_t\times\Omega_t\times r_{bt}\\ \dot{\Omega}_t&=\dot{\Omega}_b+\ddot{\theta}\mathbf{e}_3 \end{aligned} VtΩtV˙tΩ˙t=Vb+(Ωb+θ˙e3)×rbt=Ωb+θ˙e3=V˙b+Ωt×Vb+Ω˙t×rbt+Ωt×Ωt×rbt=Ω˙b+θ¨e3
其中, e 3 = [ 0 , 0 , 1 ] T \mathbf{e}_3=[0,0,1]^T e3=[0,0,1]T。
(2)鱼尾受力分析
鱼尾受到来自鱼头的 − F -F −F的力,以及 − M -M −M的力矩。利用牛顿欧拉方程:
− F = m t V ˙ t − M + r b t × F = J t Ω ˙ t + Ω t × J t Ω t \begin{aligned} -F&=m_t \dot{V}_t\\ -M+r_{bt}\times F&=J_t \dot{\Omega}_t + \Omega_t\times J_t\Omega_t \end{aligned} −F−M+rbt×F=mtV˙t=JtΩ˙t+Ωt×JtΩt
进一步整理,可得:
F = − m t V ˙ t M = − J t Ω ˙ t − Ω t × J t Ω t + r b t × F (2) \begin{aligned} F&=-m_t \dot{V}_t\\ M&=-J_t \dot{\Omega}_t - \Omega_t\times J_t\Omega_t+r_{bt}\times F \end{aligned}\tag{2} FM=−mtV˙t=−JtΩ˙t−Ωt×JtΩt+rbt×F(2)
到这里,我们可以通过联立(1)和(2)方程,求解由尾巴运动,造成的鱼头加速度了。
Note. 如果对这些公式接受起来还有困难的话,读者可以移步:
机器人动力学建模之刚体动力学基础学习
机器人动力学建模之牛顿欧拉法推导
关于机器人运动学与动力学建模的几点领悟
3 MATLAB代码实现
以下代码,完全按照上述公式进行复现。
clc;
clear all;
close all;
% 物理参数——鱼头
mb = 1.0;
Jb = 0.01;
% 物理参数——鱼尾
mt = 0.2;
Jt = 0.001;
r = 0.1;
% 关节运动
theta = 0;
dtheta = 0;
ddtheta = 0;
a = pi*2;
b = pi/4;
% 运动状态
Vb = zeros(3,1);
dVb = zeros(3,1);
Wb = zeros(3,1);
dWb = zeros(3,1);
Vt = zeros(3,1);
dVt = zeros(3,1);
Wt = zeros(3,1);
dWt = zeros(3,1);
Yaw = 0;
Pos = zeros(3,1);
% 阻力系数
CFb = 10*[0.1; 0.01; 0];
CMb = [0; 0; 1];
CFt = [0.1; 0.1; 0.1];
% 力
F = zeros(3,1);
M = zeros(3,1);
% 其他辅助变量
e3 = [0;0;1];
time = [];
The = [];
Vel = [];
WVel = [];
Poslist = [];
Flist = [];
Mlist = [];
%% 主要仿真过程
for t = 0:0.01:20
% 给定关节运动
theta = b*cos(a*t);
dtheta = -a*b*sin(a*t);
ddtheta = -a*a*b*cos(a*t);
r_bt = r*[cos(theta);sin(theta);0];
% 鱼尾速度
Wt = Wb + dtheta*e3;
Vt = Vb + cross(Wt,r_bt);
% 鱼尾加速度
dWt = dWb + ddtheta*e3;
dVt = dVb + cross(Wt,Vb) + cross(dWt,r_bt)+cross(Wt,cross(Wt,r_bt));
% 力
F = -mt*dVt;
M = cross(r_bt, F) - Jt*dWt - cross(Wt, Jt*Wt);
% 计算阻力
Fdb = -0.5*CFb.*[sign(Vb(1))*Vb(1)*Vb(1); sign(Vb(2))*Vb(2)*Vb(2); sign(Vb(3))*Vb(3)*Vb(3)];
Mdb = -0.5*CMb.*[sign(Wb(1))*Wb(1)*Wb(1); sign(Wb(2))*Wb(2)*Wb(2); sign(Wb(3))*Wb(3)*Wb(3)];
Fdt = -0.5*CFt.*[sign(Vt(1))*Vt(1)*Vt(1); sign(Vt(2))*Vt(2)*Vt(2); sign(Vt(3))*Vt(3)*Vt(3)];
% 分析头部连杆,计算鱼头加速度
dVb = (F+Fdb-mb*cross(Wb, Vb))/mb;
dWb = (M+Mdb-cross(Wb,Jb*Wb))/Jb;
% 鱼头速度更新
Vb = Vb + dVb*0.01;
Wb = Wb + dWb*0.01;
% 鱼头位置更新
Yaw = Yaw + Wb(3)*0.01;
R = [cos(Yaw), -sin(Yaw), 0;
sin(Yaw), cos(Yaw), 0;
0, 0, 1];
Vw = R*Vb;
Pos = Pos + Vw*0.01;
% 收集数据
time = [time, t];
Poslist = [Poslist, Pos];
Flist = [Flist, F];
Mlist = [Mlist, M];
Vel = [Vel, Vb];
WVel = [WVel, Wb];
end
%% 绘图
figure(1)
subplot(3,2,1)
title('力');
hold on
plot(time, Flist(1,:),'r')
ylabel('X')
grid on
subplot(3,2,3)
plot(time, Flist(2,:),'g')
ylabel('Y')
grid on
subplot(3,2,5)
plot(time, Flist(3,:),'b')
ylabel('Z')
grid on
subplot(3,2,2)
title('力矩');
hold on
plot(time, Mlist(1,:),'r')
ylabel('X')
grid on
subplot(3,2,4)
plot(time, Mlist(2,:),'g')
ylabel('Y')
grid on
subplot(3,2,6)
plot(time, Mlist(3,:),'b')
ylabel('Z')
grid on
figure(2)
subplot(3,2,1)
title('速度');
hold on
plot(time, Vel(1,:),'r')
ylabel('X')
grid on
subplot(3,2,3)
plot(time, Vel(2,:),'g')
ylabel('Y')
grid on
subplot(3,2,5)
plot(time, Vel(3,:),'b')
ylabel('Z')
grid on
subplot(3,2,2)
title('角速度');
hold on
plot(time, WVel(1,:),'r')
ylabel('X')
grid on
subplot(3,2,4)
plot(time, WVel(2,:),'g')
ylabel('Y')
grid on
subplot(3,2,6)
plot(time, WVel(3,:),'b')
ylabel('Z')
grid on
figure(3)
plot(Poslist(1,:),Poslist(2,:))
grid on
axis equal
4 仿真结果分析
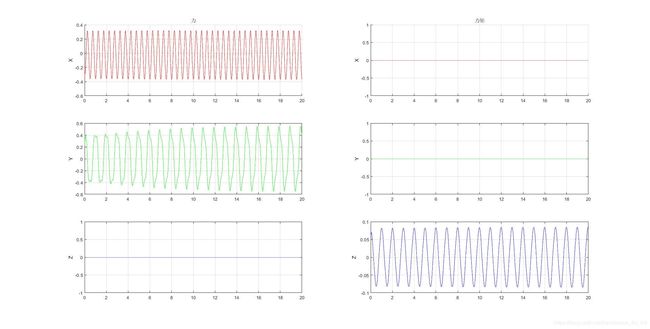
4.1 鱼头固定,只摆动鱼尾,推力的效果
X方向代表推力,根据坐标系定义,负半轴代表前进方向,可以看到,推力在正负方向上非常对称,甚至力有些往正半轴方向偏移,有些向后的力产生。所以,这种建模方法,在这种情况下,产生不了推力,和我们的经验是相违背了。毕竟,我们都知道,如果实验中把鱼头固定,用鱼尾巴拍水,也一定会产生向前的推力的。
出师不利,但是不要紧,我们继续往下看!
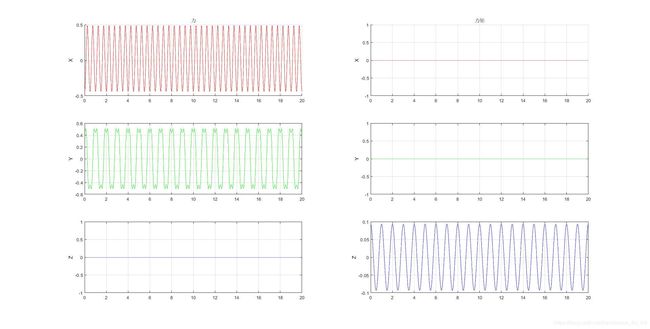
4.2 鱼头不固定,摆动鱼尾,但是不加阻力
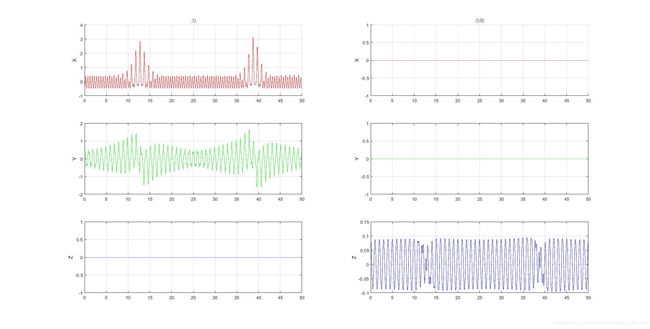
以上是力的曲线,可以看出总体上,X轴上的力有往负半轴偏移的趋势。说明,当鱼头不固定时,很有可能鱼尾的摆动会产生一定的前向力,但是有两次,分别是10s和35s的时候正向上出现了很大的力,也就是说,出现后向力的可能性也有,主要取决于鱼头当时的状态。
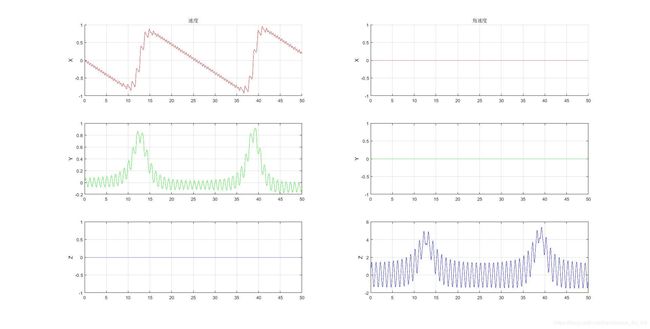
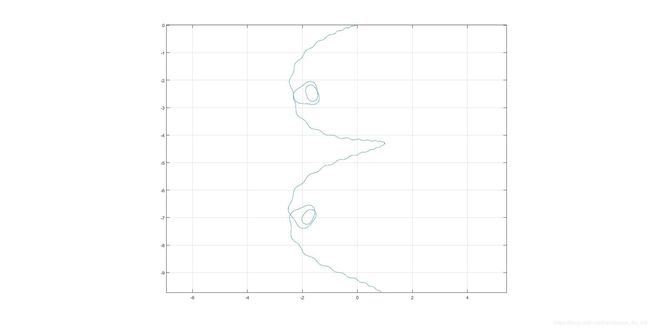
以上是速度和轨迹的图线,可以看到,鱼头是忽进忽退的,速度一会儿朝前,一会儿朝后。
综上,在这种情况下,并不能产生稳定的推力。
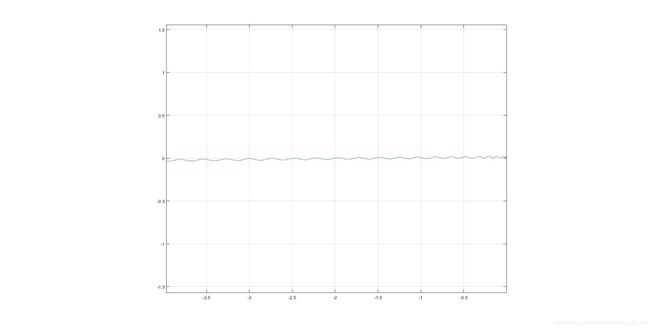
4.3 鱼头不固定,摆动鱼尾,考虑阻力
看到这里,是不是感叹,奇迹发生了!
考虑了阻力以后,X轴上的力往负半轴偏移了,速度也往负半轴方向增长,鱼游动的轨迹也成了一条直线。鱼顺利产生了推进力,和实验中观察到的现象是一致的。
究其原因,大概是,考虑阻力以后,鱼头的晃动变得可控,使得力始终保持在鱼体的轴线附近,从而产生了推进力!
5 小结
OK!
看到了这里,我们已经验证了,只考虑附加质量和阻力实际上确实可以产生推进力,而且阻力在这里起到了至关重要的作用。
但是阻力究竟是如何起作用的呢?
我也还在探索中,有了新发现再来更新吧!