深度、广度优先遍历算法python
文章目录
- 一、深度优先
- 1.怎么抓住小偷
- 2.二叉树中的最大路径和
- 3.最大的岛屿
- 二、广度优先
- 1.树的右侧
- 2.合法的括号
- 3.寻找制高点
- 4.选课的智慧
一、深度优先
该篇学习笔记来自于《你也能看得懂的python算法书》
深度优先遍历算法是经典的图论算法,从某个节点v出发开始进行搜索,不断搜索直至该节点的所有边都被遍历完。当节点v的所有边都被遍历以后,深度优先遍历算法则需要回溯到v的前驱节点,来继续搜索这个前驱节点其他边。
如果还存在尚未被遍历的节点,则深度优先遍历算法将会按照统一的规则从这些剩下的节点中选择一个节点再重复同样的遍历过程。这样的搜索过程从最开始的节点一直持续到最后一个节点的所有边都被遍历完。
1.怎么抓住小偷
问题描述:有一个绝顶狡猾的小偷瞄准了一个高档小区。这个小区的别墅以二叉树的结构坐落。除了第一栋别墅,每一栋别墅都与另一栋“源头”别墅连接。一旦小偷闯入两栋相接的别墅。警铃就会被触发。原圈里的数字代表财产,狡猾的小偷已经计划好了路线,准备在不触发警铃的前提下偷最多的钱。别墅小区的保安部门最近得到了风声,说有一个世纪大盗瞄准了别墅区。所以保安准备在小偷的必经之路上布置警卫,不动声色的抓住小偷。试确定小偷的路线,写程序输出小偷经过路线上的金额总合。
解决思路:总结规律,发现,每一个节点的偷值都是:左侧子节点的不偷值+左侧子节点的不偷值+节点的财富,每一个节点的偷值都是:左侧子节点的最大值+右侧子节点的最大值。

class Treenode(object):
def __init__(self,x,l,r):
self.value=x
self.right=r
self.left=l
def rob(root):
a=helper(root)
return max(a[0],a[1])
def helper(root):
if(root==None):
return[0,0]
left=helper(root.left)
right=helper(root.right)
robvalue=root.value+left[1]+right[1]
skipvalue=max(left[0],left[1])+max(right[0],right[1])
return(robvalue,skipvalue)
node1=Treenode(1,None,None)
node2=Treenode(3,None,None)
node3=Treenode(1,None,None)
node4=Treenode(4,node1,node2)
node5=Treenode(5,None,node3)
node6=Treenode(3,node4,node5)
solution=rob(node6)
print(solution)
#输出:9
2.二叉树中的最大路径和
问题描述:小明在怪兽的路上,怪兽们的位置以二叉树的形式展示。小明最少打一只怪兽,并且不能重复打已经交过手的怪兽。每打败一只怪兽都有相应的奖励,但如果失败也有惩罚,小明的目的是尽可能多地得到奖励,或者最少的惩罚。写一个程序,输出最大可能的路径和。
解决思路:root节点的不停值是以下三个值中的最大值:root值、root值+左子节点的不停值、root值+右子节点的不停值。root节点的停值是以下五个值中的最大值:左子节点的停值、左子节点的不停值、右子节点的停值、右子节点的不停值、root值+左右子节点的停值。

class Treenode(object):
def __init__(self,x):
self.value=x
self.right=None
self.left=None
def maxpathsum(root):
return max(helper(root))#调用helper方法,传入根节点,输出返回的两个值中的最大值
def helper(root):
if root==None:
return float('-inf'),float('-inf')#如果节点为空,返回两个最小值,表示负无穷的数
leftY,leftN=helper(root.left)#得到左子节点的不停值与停值
rightY,rightY=helper(root.right)#得到右子节点的停值与不停值
yes=max(root.value+leftY,root.value+rightY,root.value)
no=max(leftY,rightY,leftN,leftY,root.value+rightY+leftY)
return yes,no#输出[不停值,停值]
node1=Treenode(0)
node2=Treenode(-6)
node3=Treenode(6)
node4=Treenode(-2)
node1.left=None
node1.right=None
node2.left=None
node2.right=None
node3.left=node1
node2.right=node2
node4.left=node3
node4.right=None
print(maxpathsum(node4))
#输出:6
图层遍历顺序:从下往上,根节点在底部
3.最大的岛屿
问题描述:小明打算去马尔代夫度假,马尔代夫有上百个岛,小明想知道哪个是最大的岛。为了方便计算,我们使用一个二维数组来表示马尔代夫的一片海域,使用0表示水面,使用1表示陆地,目前这块区域一共有面积各不相同的5个小岛,我们需要找到其中面积最大的那个岛。
注意:岛屿是指上下左右四个方向相连接的陆地
class solution(object):
def maxAreaOfIsland(self,grid):
self.maxsum=0
row=len(grid)#存储地图的行数
col=len(grid[0])#存储地图的列数
for i in range(row):
for j in range(col):
if grid[i][j]==1:
current=1
self.dfs(i,j,current,grid)#测量岛屿的面积
return self.maxsum#最后返回最大岛屿的面积
def dfs(self,i,j,current,grid):
grid[i][j]=2#先标记此处已访问
if i>0 and grid[i-1][j]==1:#向上走考察是否越界并且是否为陆地
current=self.dfs(i-1,j,current+1,grid)
if i<len(grid)-1 and grid[i+1][j]==1:
current=self.dfs(i+1,j,current+1,grid)
if j>0 and grid[i][j-1]==1:
current=self.dfs(i,j-1,current+1,grid)
if j<len(grid[0])-1 and grid[i][j+1]==1:
current=self.dfs(i,j+1,current+1,grid)
self.maxsum=max(self.maxsum,current)#更新最大面积变量
return current
grid=[[0,0,0,0,1,1,0],
[0,1,1,0,1,1,0],
[0,1,1,0,0,0,0],
[0,0,1,0,0,1,1],
[0,0,0,0,0,0,0],
[0,0,1,1,0,0,0],
[0,0,0,1,0,0,1]]
print(solution().maxAreaOfIsland(grid))
#输出:5
二、广度优先
广度优先遍历与深度优先遍历类似,也是查询的方法之一,它也是从某个状态出发查询可以到达的所有状态。但不同于深度优先遍历,广度优先遍历总是先去查询距离初始状态最近的状态。
1.树的右侧
问题描述:秋天,采摘园的柠檬都熟了,小明和小伙伴相约去采摘园摘柠檬。为了提高采摘速度,小明和贝贝约定每人采摘每棵树一半的柠檬,同时为了可持续发展,只采摘柠檬树最外层的柠檬。加入柠檬树的每个树干只有两个树枝、一个树枝、零个树枝三种可能,那么一棵树可被看做一棵二叉树。
解决思路:对于以下柠檬树,将输出每层最右侧节点,即[1,3,7,10]
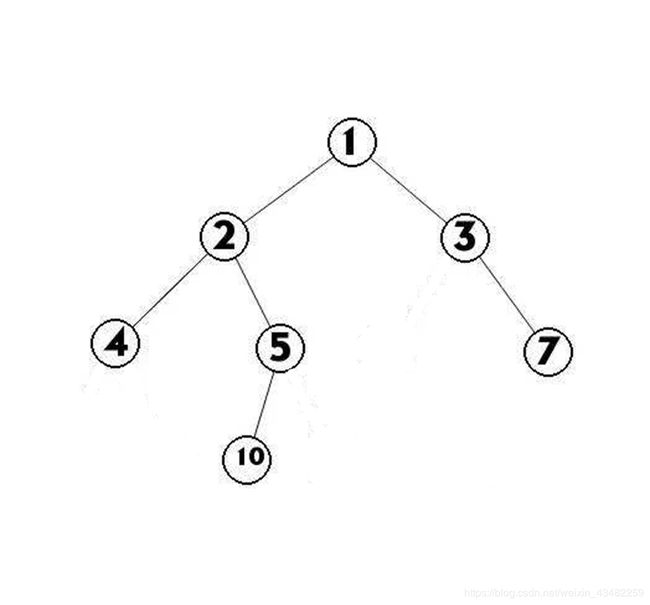
class Treenode(object):
def __init__(self,x):
self.value=x
self.right=None
self.left=None
def Treeright(root):
result=[]
queue=[root]
while len(queue)>0:
length=len(queue)
for i in range(length):
node=queue.pop(0)#取出队列头的点,pop()默认移除列表中的最后一个元素
if i==length-1:
result.append(node.value)#每层最右端的点加入数组
if node.left!=None:
queue.append(node.left)
if node.right!=None:
queue.append(node.right)
return result
#以下为测试代码
node1=Treenode(1)
node2=Treenode(2)
node3=Treenode(3)
node4=Treenode(4)
node5=Treenode(5)
node6=Treenode(7)
node7=Treenode(10)
node1.left=node2
node1.right=node3
node2.left=node4
node2.right=node5
node5.left=node7
node3.right=node6
solution=Treeright(node1)
print(solution)
#输出:[1,3,7,10]
2.合法的括号
问题描述:为了帮助老师更快的修改学生的括号匹配问题,小明决定开发一个小程序,来寻找正确的小括号组合。
解决思路:每次从队列中取出一个字符串,查看它是不是合法的,如果它是合法的,则把它加入结果集,返回结果;如果不合法,遍历这个字符串,只要遇到左右括号字符的时候,我们就去掉该括号字符生成一个新的字符串,把它也加入到队列中进行分析。
def isValid(str):
count=0
for c in str:
if c=='(':
count+=1
elif c==')':
count-=1
if count<0:
return False
return count==0
def bfs(str):
result=[]#result存放最终结果
queue=[str]
while len(queue)>0:
for i in range(len(queue)):
if isValid(queue[i]):
result.append(queue[i])
if len(result)>0:
return list(set(result))
tem=[]#建立临时结果集
for s in queue:#取出队列中的一个字符串
for i in range(len(s)):
if s[i]=='(' or s[i]==')':
tem.append(s[:i]+s[i+1:])
queue=list(set(tem))#删除上一层里的元素
return list(set(result))#先把数组转化为集合再转化为数组,达到去重的效果
print(bfs("(a)(b)))"))
#输出:['(a)(b)', '(a(b))']
每个生成的子节点就是对应每个位置移除左括号或右括号后剩下的子字符串
3.寻找制高点
问题描述:又到了春暖花开的季节,学校组织同学们去爬香山,小明和小伙伴们约定要走遍所有的制高点,他们找到香山的地图开始分析要占领哪些山头。他们拿到的地图是一张海拔图,上面有每个地理位置的海拔数据高度。为了描述这张地图,我们使用一个MxM二维数组来表示,每个点的海拔用数字来表示。如下图所示。
| 1 | 3 | 2 |
3 | 5 |
|---|---|---|---|---|
3 |
4 |
5 |
6 | 3 |
| 2 | 7 | 4 |
3 |
3 |
| 5 | 2 | 2 |
3 | 1 |
解决思路:制高点是可以一直向下到达东西南北四个方向的点,在向下走的过程中是不能爬坡的。如上图所示(以5为例),5、6、7点都是制高点,它们可以通过图中加粗的点走到四个边缘点。拿到这个题,首先想到的肯定是从每个点出发搜索是否能到达四个边缘。但是,不像迷宫,搜索的目标点不是一个单点,而是所有的边缘点,按照这种思路明显效率是很低的。那么如何来优化算法呢?换一个角度来思考,逆向思维,既然从每个点走向边缘点的效率会比较低,那么以边缘点作为起点向内部开始遍历搜寻,看下一个节点的高度是否大于或等于自身的高度。然后标记那些能够到达的点位True,按照同样的思路分别标记从四个边缘出发可以到达的点,最终四个都为True的点,就是我们寻找的最高点。
def bfs(set,m,n,matrix):
queue=list(set)#将集合转化为列表
dir=[[1,0],[-1,0],[0,1],[0,-1]]#数组中四个元素代表四个方向
while len(queue)>0:
x,y=queue.pop()
for d in dir:
xn=x+d[0]
yn=y+d[1]
if xn>=0 and xn<m and yn>=0 and yn<n:#如果新的点符合要求就把它加入队列
if matrix[xn][yn]>=matrix[x][y]:
if(xn,yn)not in set:
queue.append((xn,yn))
set.add((xn,yn))
def solve(matrix):
if not matrix:
return matrix
m=len(matrix)
n=len(matrix[0])
toppoint=set([(0,y) for y in range(n)])#set()函数接受一个列表,输出一个集合
bottompoint=set([(m-1,y)for y in range(n)])
leftpoint=set([(x,0)for x in range(m)])
rightpoint=set([(x,n-1)for x in range(m)])
bfs(toppoint,m,n,matrix)
bfs(bottompoint,m,n,matrix)
bfs(leftpoint,m,n,matrix)
bfs(rightpoint,m,n,matrix)
result=toppoint&bottompoint&leftpoint&rightpoint#求集合的交集,即从各个方向都向上的点
return result
matrix=[[1,3,2,3,5],[3,4,5,6,3],[2,7,4,3,3],[5,2,2,3,1]]
print(solve(matrix))
#输出:{(1, 2), (1, 3), (2, 1)}
集合和数组很很像,它和数组的区别是集合内部没有重复的数据
4.选课的智慧
问题描述:新学期伊始,小明正在面临选课问题,我们要学习计算机基础,数学,英语,算法,Java五门课,其中学习算法前需要先学习Java、英语,学习Java前又要先学习计算机基础和数学,那么小明该如何选课呢?
解决思路:我们给每一课设置一个编号,编号从0开始。先修课的关系如何表达呢,课程与课程之间的依赖关系以一个二维数组的形式给出,如下表所示。例如数组中第1行第3列的1表示课程0是课程2的先修课。
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 |
0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 |
def bfs(sumcourse,prelist):
prelistcount=[0]*sumcourse#对每门课程先修课数量的数组初始化
for line in prelist:#取出二维数组的每一行
for i in range(len(line)):#针对每一行的prelistcount赋值
if line[i]==1:
prelistcount[i]+=1
canmake=[]
for i in range(len(prelistcount)):
if prelistcount[i]==0:
canmake.append(i)#存放进目前可以选修课程的队列
classmake=[]
while len(canmake)!=0:
thisclass=canmake[0]
del canmake[0]
classmake.append(thisclass)
for i in range(sumcourse):
if prelist[thisclass][i]==1:
prelistcount[i]-=1
if prelistcount[i]==0:#如果一门课的先修课为0,就将其加入队列
canmake.append(i)
return classmake
print(bfs(5,[[0,0,1,0,0],[0,0,1,0,0],[0,0,0,0,1],[0,0,0,0,1],[0,0,0,0,0]]))
#输出:[0, 1, 3, 2, 4]
通过以上方法得到的选课列表不是唯一的。