scipy库中的leastsq函数
只需要输入一系列样本点,给出待求函数的基本形状(如二元二次函数就是一种形状
f(x,y)=w0x^2 + w1y^2 + w2xy + w3x + w4y + w5
在形状给定后,我们只需要求解相应的系数w0~w5),即可得到相应的参数。至于中间到底是怎么求的,这一部分内容就像一个黑箱一样。
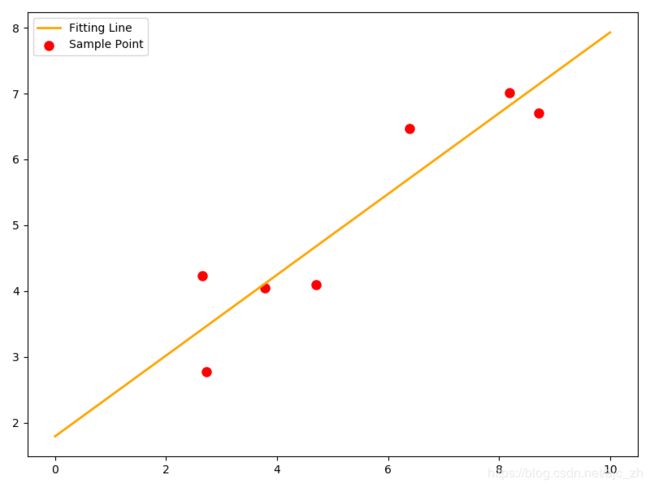
则使用leastsq函数求解其拟合直线的代码如下:
###最小二乘法试验###
import numpy as np
from scipy.optimize import leastsq
###采样点(Xi,Yi)###
Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
###需要拟合的函数func及误差error###
def func(p,x):
k,b=p
return k*x+b
def error(p,x,y,s):
print (s) #看打印多少条s,就是leastsq调用了多少次error函数
return func(p,x)-y #x、y都是列表,故返回值也是个列表
#p0存放k、b的初始值,这个值可以随意指定
p0=[100,2]
#print( error(p0,Xi,Yi) )
###主函数从此开始###
s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的k、b
Para = leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中
print(Para) # (array([0.61349535, 1.79409255]), 3)
k,b = Para[0]
print("k=",k,'\n',"b=",b) # k= 0.6134953462154726 b= 1.7940925542913093
###绘图,看拟合效果###
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点
x=np.linspace(0,10,1000)
y=k*x+b
plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2) #画拟合直线
plt.legend()
plt.show()
1、p0里放的是k、b的初始值,这个值可以随意指定。往后随着迭代次数增加,k、b将会不断变化,使得error函数的值越来越小。
2、func函数里指出了待拟合函数的函数形状。
3、error函数为误差函数,我们的目标就是不断调整k和b使得error不断减小。这里的error函数和神经网络中常说的cost函数实际上是一回事,只不过这里更简单些而已。
4、必须注意一点,传入leastsq函数的参数可以有多个,但必须把参数的初始值p0和其它参数分开放。其它参数应打包到args中。
5、leastsq的返回值是一个tuple,它里面有两个元素,第一个元素是k、b的求解结果,第二个元素暂时不知道是什么意思,先留下来。
以上参考:
Python闲谈(二)聊聊最小二乘法以及leastsq函数
https://www.cnblogs.com/NanShan2016/p/5493429.html
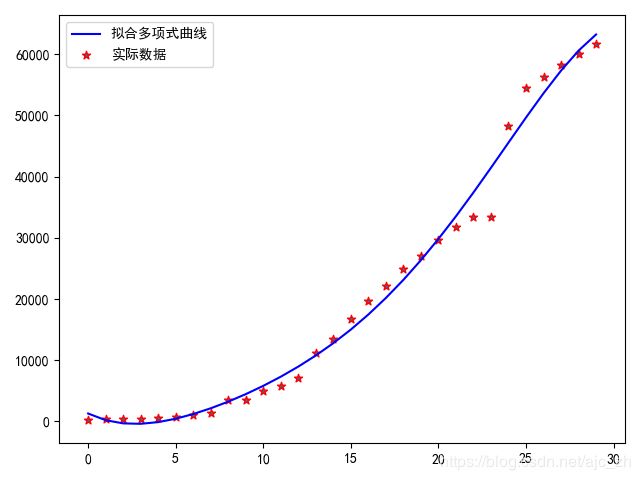
使用p次多项式拟合,疫情以来,武汉累积确诊病例的数据
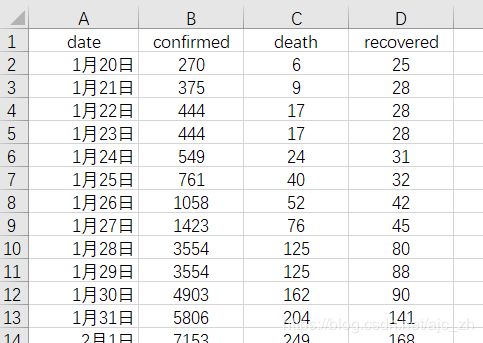
文件:武汉累积数据.xlsx
日期 累积确诊 累积死亡 累积出院
from scipy.optimize import leastsq ##引入最小二乘法算法
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# % matplotlib
# inline
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def error(p, x, y):
fun = np.poly1d(p)
# poly1d()函数可以按照输入的列表p返回一个多项式函数
# 这里设计了一个poly1d()函数,关于这个函数,简单理解下就是输入一个列表,返回以这个列表中的值为参数的多项式,例如:
# 输入:p=[1,2,3]
# 返回:x^2 + 2x + 3
return y - fun(x)
# 拟合函数
def fitting(p):
pars = np.random.rand(p+1) # 生成p+1个随机数的列表,这样poly1d函数返回的多项式次数就是p,作为初值
r = leastsq(error, pars, args=(Xi,Yi)) # 三个参数:误差函数、函数参数列表、数据点
return r
data = pd.read_excel('武汉累积数据.xlsx')
Yi = data['confirmed'].values[:30] #获取前30行的confirmed确诊数据
Xi = data.index.values[:30]
fit_pars = fitting(5)[0] #这里使用5次多项式去拟合实际数据,取返回值r的第一个元素,该元素就是多项式的系数
print(fit_pars) #得出多项式 [-1.74500210e-02 1.15126287e+00 -2.68322791e+01 3.58227740e+02 -1.42370074e+03 1.30423560e+03]
plt.plot(Xi, np.poly1d(fit_pars)(Xi),color='blue', label='拟合多项式曲线')
plt.scatter(Xi,Yi,edgecolors='red',marker='*',label='实际数据点')
plt.legend()
plt.show()