投影矩阵的推导(Deriving Projection Matrices)
文章目录
- 概述: 什么是投影?
- 正交投影(Orthographic Projection)
- 透视投影(Perspective Projection)
- 总结
原文:Deriving Projection Matrices
在学习 LearnGL - 学习笔记目录 之前找过一些关于 透视矩阵 的教程,发现有很多写的不错的文章,如:OpenGL Transformation,但这里我只列出一个写的 最清晰 的,就上面原文的内容 Deriving Projection Matrices,因为作者将每一项的推导过程写的相当详细,如果你想了解过程,真的不要错过,这里我转载一下译文,便于大家的理解,译者是:流星上的潴 ,但是我已经找不到原文了,在此感谢原文作者写出这么好的文章,也感谢译者翻译得不错!
本文除了转载译文之外,还将原来的图片公式换成了,LaTex 公式,看着舒服一些
在3D图形程序的基本矩阵变换中,投影矩阵是其中比较复杂的。平移和缩放浏览一下就能理解,旋转矩阵只要掌握了三角函数知识也可以理解,但投影矩阵有点棘手。如果你曾经看过投影矩阵,你会发现你的常识不足以告诉你它是怎么来的。而且,我在网上还未看到许多关于如何推导投影矩阵的教程资源。本文的话题就是如何推导投影矩阵。
对于刚刚开始接触3D图形的人,我应该指出,理解投影矩阵如何推导可能是我们对于数学的好奇心,它不是必须的。你可以只用公式,并且如果你用像Direct3D那样的图形API,你甚至都不需要使用公式,图形API会为你构建一个投影矩阵。所以,如果本文看起来有点难,不要害怕。只要你理解了投影矩阵做了什么,你没必要在你不想的情况下关注它是怎么做的。本文是给那些想了解更多的程序员的。
概述: 什么是投影?
计算机显示器是一个二维表面,所以如果你想显示三维图像,你需要一种方法把3D几何体转换成一种可作为二维图像渲染的形式。那也正是投影做的。拿一个简单的例子来说,一种把3D对象投影到2D表面的方法是简单的把每个坐标点的z坐标丢弃。对立方体来说,看上去可能像图1:

图1: 通过丢弃Z坐标投影到XY平面
当然,这过于简单,并且在大多数情况下不是特别有用。首先,根本不会投影到一个平面上;相反,投影公式将变换你的几何体到一个新的空间体中,称为规范视域体(canonical view volume),规范视域体的精确坐标可能在不同的图形API之间互不相同,但作为讨论起见,把它认为是从(-1, -1, 0)延伸至(1, 1, 1)的盒子,这也是Direct3D中使用的。一旦所有顶点被映射到规范视域体,只有它们的x和y坐标被用于映射到屏幕上。这并不代表z坐标是无用的,它通常被深度缓冲用于可见度测试。这就是为什么变换到一个新的空间体中,而不是投影到一个平面上。
注意,图1描述的是左手坐标系,摄像机俯视z轴正方向,y轴朝上并且x轴朝右。这是Direct3D中使用的坐标系,本文中我都将使用该坐标系。对于右手坐标系系统来说,在计算方面没有明显差异,在规范视域体方面有一点区别,所以一切讨论仍将适用即使你的图形API使用与Direct3D不同的规定。
现在,可以进入实际的投影变换了。有许多投影方法,我将介绍最常见的2种:正交和透视。
正交投影(Orthographic Projection)
正交投影,之所以这么称呼是因为所有的投影线都与最终的绘图表面垂直,是一种相对简单的投影技术。视域体,也就是包含所有你想显示的几何体的可视空间——是一个将被变换到规范视域体的轴对齐盒子,见图2:

图2: 正交投影
正如你看见的,视域体由6个面定义:
left : x = l x=l x=l
right : x = r x=r x=r
bottom : y = b y=b y=b
top : y = t y=t y=t
near : z = n z=n z=n
far : z = f z=f z=f
因为视域体和规范视域体都是轴对齐盒子,这种类型的投影没有距离更正。最终的结果是,事实上,很像图1那样每个坐标点只是丢弃了z坐标。对象在3D空间中的大小和在投影中的大小相同,即使一个对象比另一个对象距离摄像机远很多。在3D空间中平行的直线在最终的图像上也是平行的。使用这种类型的投影将出现一些问题像第一人称射击游戏——试想一下在不知道任何东西有多远的情况下玩!但它也有它的用处。你可能在格子游戏中使用它,例如,特别是摄像机被绑定在一个固定角度的一款格子游戏中,图3显示了1个简单的例子:

图3: 正交投影的一个简单例子
所以,事不宜迟,现在开始弄清楚它是如何工作的。最简单的方法可能是3个坐标轴分开考虑,并且计算如何沿着每个坐标轴将点从视域体映射到规范视域体。从x轴开始,视域体中的点的x坐标范围在[l, r],想把它变换到范围在[-1, 1]:
l ≤ x ≤ r l \le x \le r l≤x≤r
现在,准备把范围缩小到我们期望的,各项减去l,这样,最左边的项变为0。另一种可能考虑的做法是平移范围使其以0为中心,而不是一端为0,但现在这种方式代数式更整洁,所以为了可读性起见我将以现在这种方式做:
0 ≤ x − l ≤ r − l 0 \le x-l \le r-l 0≤x−l≤r−l
现在,范围的一端是0,你可以缩小到期望的大小。你期望x值的范围是2个单位宽,从1到-1,所以把各项乘以2/(r-l)。注意r-l是视域体的宽度,因此始终是一个正数,所以不用担心不等号会改变方向:
0 ≤ 2 x − 2 l r − l ≤ 2 0 \le \frac{2x-2l}{r-l} \le 2 0≤r−l2x−2l≤2
下一步,各项减去1就产生了我们期望的范围[-1,1]:
− 1 ≤ 2 x − 2 l r − l − 1 ≤ 1 -1 \le \frac{2x-2l}{r-l}-1 \le 1 −1≤r−l2x−2l−1≤1
基本代数允许我们将中间项写成一个单一的分数:
− 1 ≤ 2 x − r − l r − l ≤ 1 -1 \le \frac{2x-r-l}{r-l} \le 1 −1≤r−l2x−r−l≤1
最后,把中间项分成两部分使它形如px+q的形式,我们需要把项组织成这种形式这样我们推导的公式就可以简单的转换成矩阵形式:
− 1 ≤ 2 x r − l − r + l r − l ≤ 1 -1 \le \frac{2x}{r-l}-\frac{r+l}{r-l} \le 1 −1≤r−l2x−r−lr+l≤1
这个不等式的 中间项 告诉了我们把x转换到规范视域体的公式:
x ′ = 2 x r − l − r + l r − l x'=\frac{2x}{r-l}-\frac{r+l}{r-l} x′=r−l2x−r−lr+l
获取y的变换公式的步骤是完全一样的——只要用y替代x,用t替代r,用b替代l——所以这里不重复它们了,只是给出结果:
y ′ = 2 y t − b − t + b t − b y'=\frac{2y}{t-b}-\frac{t+b}{t-b} y′=t−b2y−t−bt+b
最后,需要推倒z的变换公式。z的推导有点不同,因为需要把z映射到范围[0, 1]而不是[-1, 1],但看上去很相似。z坐标最开始在范围[n,f]:
n ≤ z ≤ f n \le z \le f n≤z≤f
把各项减去n,这样的话范围的下限就变为了0:
0 ≤ z − n ≤ f − n 0 \le z-n \le f-n 0≤z−n≤f−n
现在剩余要做的就是除以f-n,这样就产生了最终的范围[0,1]。和前面相同,注意f-n是视域体的深度所以绝对不会为负:
0 ≤ z − n f − n ≤ 1 0 \le \frac{z-n}{f-n} \le 1 0≤f−nz−n≤1
最后,把它分成两部分使它形如px+q的形式:
0 ≤ z f − n − n f − n ≤ 1 0 \le \frac{z}{f-n}-\frac{n}{f-n} \le 1 0≤f−nz−f−nn≤1
这样便给出了z的变换公式
z ′ = z f − n − n f − n z'=\frac{z}{f-n}-\frac{n}{f-n} z′=f−nz−f−nn
现在,可以准备写正交投影矩阵了。总结到目前为止的工作,推导了3个投影公式:
x ′ = 2 x r − l − r + l r − l x'=\frac{2x}{r-l}-\frac{r+l}{r-l} x′=r−l2x−r−lr+l
y ′ = 2 y t − b − t + b t − b y'=\frac{2y}{t-b}-\frac{t+b}{t-b} y′=t−b2y−t−bt+b
z ′ = z f − n − n f − n z'=\frac{z}{f-n}-\frac{n}{f-n} z′=f−nz−f−nn
如果写成矩阵形式,就得到了:
P o = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 1 f − n − n f − n 0 0 0 1 ] P_o=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\\\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n} \\\\ 0 & 0 & 0 & 1 \end{bmatrix} Po=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡r−l20000t−b20000f−n10−r−lr+l−t−bt+b−f−nn1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
就是这样!Direct3D提供了D3DXMatrixOrthoOffCenterLH()(what a mouthful!)方法构造一个和这个公式相同的正交投影矩阵;你可以在DirectX文档中找到。方法名中的"LH"代表了你正在使用左手坐标系。但是,究竟"OffCenter"的意思是什么呢?
这一问题的答案引导你到一个正交投影矩阵的简化形式。考虑几点: 首先,在可见空间中,摄像机定位在原点并且沿着z轴方向观看。第二,你通常希望你的视野在左右方向上延伸的同样远,并且在z轴的上下方向上也延伸的同样远。如果是这样的情况,那么z轴正好直接穿过你视域体的的中心,所以得到了r = -l并且t = -b。换句话说,你可以把r, l, t和b一起忘掉,简单的把视域体定义为1个宽度w和1个高度h,以及裁剪面f和n。如果你在正交投影矩阵中应用上面说的,那么你将得到这个相当简化的版本:
P o = [ 2 w 0 0 0 0 2 h 0 0 0 0 1 f − n − n f − n 0 0 0 1 ] P_o=\begin{bmatrix} \frac{2}{w} & 0 & 0 & 0 \\\\ 0 & \frac{2}{h} & 0 & 0 \\\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n} \\\\ 0 & 0 & 0 & 1 \end{bmatrix} Po=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡w20000h20000f−n1000−f−nn1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
这个公式是Direct3D中D3DXMatrixOrthoLH()方法的实现。你几乎可以一直使用这个矩阵替代上面那个你推导的更通用的"OffCenter"版本,除非你用投影做些奇怪的事情。
在完成这部分之前还有一点。它启发我们注意到这个矩阵可以用两个简单的变换串联替代:平移其次是缩放。如果你思考几何的话这对你是有意义的,因为所有你在正交投影中做的就是从一个轴对齐盒子转向另一个轴对齐盒子;视域体不改变它的形状,只改变它的位置和大小。具体来说,有:
P o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 1 f − n 0 0 0 0 1 ] ⋅ [ 1 0 0 0 0 1 0 0 0 0 1 − n 0 0 0 1 ] P_o= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\\\ 0 & \frac{2}{t-b} & 0 & 0 \\\\ 0 & 0 & \frac{1}{f-n} & 0 \\\\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 & -n \\\\ 0 & 0 & 0 & 1 \end{bmatrix} Po=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡r−l20000t−b20000f−n100001⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤⋅⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡10000100001000−n1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
这种投影方式可能更直观一点因为它让你更容易想象发生了什么。首先,视域体沿着z轴平移使它的近平面和原点重合;然后,应用一个缩放把它缩小到规范视域体大小。很容易理解吧,对不对?一个偏离中心(OffCenter)的正交投影矩阵也可以用一个变换和一个缩放代替,它和上面的结果很相似所以我在这里不列出了。
上面就是正交投影,现在可以去接触一些更有挑战性的东西了。
透视投影(Perspective Projection)
透视投影是稍复杂的一种投影方法,并且用的越来越平凡,因为它创造了距离感,因此会生成更逼真的图像。从几何上说,这种方法与正交投影不同的地方在于透视投影的视域体是一个平截头体——也就是,一个截断的金字塔,而不是一个轴对称盒子。见图4:
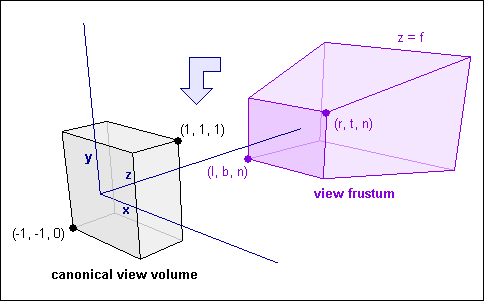
图4: 透视投影
正如你所看见的,视域体的近平面从(l,b, n)延伸至(r, t, n)。远平面范围是从原点发射穿过近平面四个点的射线直至与平面z=f相交。由于视域体从原点进一步延伸,它变得越来越宽大;同时你将这个形状变换到规范视域体盒子;视域体的远端比视域体的近端压缩的更厉害。因此,视域体远端的物体会变得更小,这就给了你距离感。
由于空间体形状的这种变换,透视投影不能像正交投影那样简单的表达为一个平移和一个缩放。你必须制定一些不同的东西。但是,这并不意味着你在正交投影上做的工作是无用的。一个方便的解决数学问题的方法是把问题减少到你已经知道怎么解决的那一个。所以,这就是你在这里可以做的。上一次,你一次检查一个坐标,但这次,你将把x和y坐标合起来一起做,然后再考虑z坐标。你对x和y的处理可以分2个步骤:
第1步: 给定视域体中的点(x,y, z),把它投影到近平面z=n。由于投影点在近平面上,所以它的x坐标范围在[l, r],y坐标范围在[b, t]。
第2步: 使用你在正交投影中学会推导的公式,把x坐标从[l, r]映射到[-1, 1],把y坐标范围从[b, t]映射到[-1, 1]。
听上去很棒吧?看一看图5:
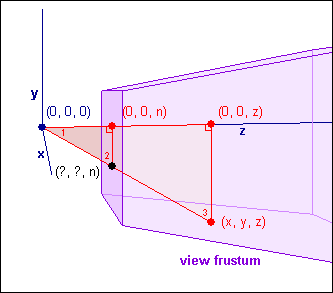
图5: 使用相似三角形投影一个点到z=n平面
在这个图中,你从点(x, y, z)到原点画了条直线,注意直线与z=n平面相交的那个点——用黑色标记的那个。通过这些点,你画了2条相对于z轴的垂线,突然你得到了一对相似三角形。如果你能够回想起高中的几何知识,相似三角形是拥有相同形状但大小不一定相同的三角形。为了证明2个三角形是相似的,必须证明它们的同位角相等,在这里不难做到。角1被两个三角形共享,显然它和自身相等。角2和角3是穿越两条平行线形成的同位角,所以它们是相等的。同时,直角当然是彼此相等的,所以两个三角形是相似的。
对于相似三角形你应该感兴趣的是它们的每对对应边都是同比例的。你知道沿着z轴的边的长度,它们是n和z。那意味着其他对应边的比例也是n/z。所以,考虑下你知道了什么。根据勾股定理,从(x, y, z)相对于z轴做的垂线具有以下长度:
L = x 2 + y 2 L=\sqrt{x^2+y^2} L=x2+y2
如果你知道了从你的投影点到z轴的垂线的长度,那么你就可以计算出该点的x和y坐标。长度怎么求?那太简单了!因为你有了相似三角形,所以长度就是简单的L乘以n/z:
L 2 = n z x 2 + y 2 L2=\frac{n}{z}\sqrt{x^2+y^2} L2=znx2+y2
L 2 = n 2 z 2 ( x 2 + y 2 ) L2=\sqrt{\frac{n^2}{z^2}(x^2+y^2}) L2=z2n2(x2+y2)
L 2 = ( x n z ) 2 + ( y n z ) 2 L2=\sqrt{(\frac{xn}{z})^2+(\frac{yn}{z})^2} L2=(zxn)2+(zyn)2
因此,x坐标是x * n/z,y坐标是y * n/z。第一步做完了。
第二步只是简单的执行你上一部分做的同样的映射,所以是时候回顾下你在正交投影中学习到的推导公式了。回想下把x和y坐标映射到规范视域体,像这样:
x ′ = 2 x r − l − r + l r − l x'=\frac{2x}{r-l}-\frac{r+l}{r-l} x′=r−l2x−r−lr+l
y ′ = 2 y t − b − t + b t − b y'=\frac{2y}{t-b}-\frac{t+b}{t-b} y′=t−b2y−t−bt+b
现在你可以再次调用这些公式,除非你要考虑到投影;所以,把x用x * n/z代替,把y用y * n/z代替:
x ′ = ( 2 n r − l ) x z − r + l r − l x'=(\frac{2n}{r-l})\frac{x}{z}-\frac{r+l}{r-l} x′=(r−l2n)zx−r−lr+l
y ′ = ( 2 n t − b ) y z − t + b t − b y'=(\frac{2n}{t-b})\frac{y}{z}-\frac{t+b}{t-b} y′=(t−b2n)zy−t−bt+b
现在,通过乘以z:
x ′ z = 2 n r − l x − r + l r − l z x'z=\frac{2n}{r-l}x-\frac{r+l}{r-l}z x′z=r−l2nx−r−lr+lz
y ′ z = 2 n t − b y − t + b t − b z y'z=\frac{2n}{t-b}y-\frac{t+b}{t-b}z y′z=t−b2ny−t−bt+bz
这些结果有点奇怪。为了把这些等式写进矩阵,你需要把它们写成这种形式:
x ′ = c 1 x + c 2 y + c 3 z + c 4 x'=c_1x+c_2y+c_3z+c_4 x′=c1x+c2y+c3z+c4
y ′ = c 5 x + c 6 y + c 7 z + c 8 y'=c_5x+c_6y+c_7z+c_8 y′=c5x+c6y+c7z+c8
但很明显,现在还做不到,所以现在看起来进入了僵局。应该做什么呢?如果你能找到个办法获得z’z的公式就像x’z和y’z那样,你就可以写一个变换矩阵把(x, y, z)映射到(x’z, y’z, z’z)。然后,你只需要把各部分除以点z,你就会得到你想要的(x’, y’, z’)。
因为你知道z到z’的转换不依赖于x和y,你知道你想要一个公式形如z’z= pz + q,p和q是常量。并且,你可以很容易的找到那些常量,因为你知道在两种特殊情况下如何得到z’: 因为你要把[n, f]映射到[0, 1],你知道当z=n时z’=0,和z=f时z’=1。当你把第一组值代入z’z = pz + q,你可以解得:
0 = p n + q 0=pn+q 0=pn+q
q = − p n q=-pn q=−pn
现在,把第二组值代入,得到:
f = p f + q f=pf+q f=pf+q
把q的值代入等式,你可以很容易的解得p:
f = p f − p n f=pf-pn f=pf−pn
f = p ( f − n ) f=p(f-n) f=p(f−n)
p = f f − n p=\frac{f}{f-n} p=f−nf
现在你有p的值了,并且刚刚你求得了q= –pn,所以你可以解得q:
q = − f n f − n q=-\frac{fn}{f-n} q=−f−nfn
最后,把p和q的表达式代入最原始的公式中,得:
z ′ z = f f − n z − f n f − n z'z=\frac{f}{f-n}z-\frac{fn}{f-n} z′z=f−nfz−f−nfn
你就快完成了,但是你处理这个问题的不寻常的性质需要你也处理齐次坐标w。通常情况下,只是简单的设置w’ = 1 ——你可能已经注意到在一个基本的变换下最后一行总是[0, 0, 0, 1]—但是现在你在为点(x’z, y’z, z’z, w’z)写一个变换。所以取而代之的,把w’ = 1写成w’z = z。因此最后用于透视投影的等式如下:
x ′ z = 2 n r − l x − r + l r − l z x'z=\frac{2n}{r-l}x-\frac{r+l}{r-l}z x′z=r−l2nx−r−lr+lz
y ′ z = 2 n t − b y − t + b t − b z y'z=\frac{2n}{t-b}y-\frac{t+b}{t-b}z y′z=t−b2ny−t−bt+bz
z ′ z = f f − n z − f n f − n z'z=\frac{f}{f-n}z-\frac{fn}{f-n} z′z=f−nfz−f−nfn
w ′ z = z w'z=z w′z=z
现在,当你把这个等式写成矩阵的形式,得到:
P p = [ 2 n r − l 0 − r + l r − l 0 0 2 n t − b − t + b t − b 0 0 0 f f − n − f n f − n 0 0 1 0 ] P_p=\begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n} \\\\ 0 & 0 & 1 & 0 \end{bmatrix} Pp=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡r−l2n0000t−b2n00−r−lr+l−t−bt+bf−nf100−f−nfn0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
当你把这个矩阵用于点(x, y, z,1),它将产生(x’z, y’z, z’z, w’z)。然后,你应用通常的步骤去除以齐次坐标,得到(x’, y’, z’, 1)。那就是透视投影。Direct3D的D3DXMatrixPerspectiveOffCenterLH()方法也实现了上述公式。正如正交投影,如果你假设视域体是对称的并且中心是z轴(也就是r = -l,t = -b),你可以简单的用视域体的宽w和高h改写矩阵中的各项:
P p = [ 2 n w 0 0 0 0 2 n h 0 0 0 0 f f − n − f n f − n 0 0 1 0 ] P_p=\begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\\\ 0 & \frac{2n}{h} & 0 & 0 \\\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n} \\\\ 0 & 0 & 1 & 0 \end{bmatrix} Pp=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡w2n0000h2n0000f−nf100−f−nfn0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
Direct3D的D3DXMatrixPerspectiveLH()方法也生成这个矩阵。
最后,还有个经常用的上的透视投影的表示。在这种表示中,你根据摄像机的可视范围定义视域体,而不用去担心视域体的尺寸。此概念参阅图6:

图6: 视域体的高由垂直可视范围的角度a定义
垂直可视范围的角度是a。这个角度被z轴一分为二,所以根据基本的三角函数,你可以写下面的方程,关联a和近平面n以及屏幕高度h:
cot a 2 = 2 n h \cot\frac{a}{2}=\frac{2n}{h} cot2a=h2n
这个表达式可以取代投影矩阵中的高度。此外,使用横纵比r代替宽度,r定义为显示区域的宽比高的横纵比。所以,得到:
2 n w = 2 n r h = 1 r cot a 2 \frac{2n}{w}=\frac{2n}{rh}=\frac{1}{r}\cot\frac{a}{2} w2n=rh2n=r1cot2a
因此,有了用垂直可视范围角度a和横纵比r构成的透视投影矩阵:
P p = [ 1 r cot a 2 0 0 0 0 cot a 2 0 0 0 0 f f − n − f n f − n 0 0 1 0 ] P_p=\begin{bmatrix} \frac{1}{r}\cot\frac{a}{2} & 0 & 0 & 0 \\\\ 0 & \cot\frac{a}{2} & 0 & 0 \\\\ 0 & 0 & \frac{f}{f-n} & -\frac{fn}{f-n} \\\\ 0 & 0 & 1 & 0 \end{bmatrix} Pp=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡r1cot2a0000cot2a0000f−nf100−f−nfn0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
在Direct3D中,你可以使用D3DXMatrixPerspectiveFovLH()方法得到这种形式的矩阵。这种形式特别有用,因为你可以直接把r设置成渲染窗口的横纵比,并且可视范围角度为p / 4比较好。所以,你真正需要担心的事情只是定义视域体沿着z轴的范围。
总结
这就是所有的你需要的投影变换背后的数学概念。还有一些其他的不太常用的投影方法,并且如果你使用右手坐标系或者一个不同的规范视域体就会和我们讨论的有点不同,但是以本文的结论作为基础你应该很容易能够推导出那些公式。如果你想知道更多的关于投影或者其他变换的信息,看一看Tomas Moller和Eric Haines的Real-Time Rendering,或者James D. Foley, Andries van Dam, Steven K. Feiner和John F.Hughes的Computer Graphics: Principles and Practice;这两本是优秀的关于计算机图形的书。
如果你对本文有任何问题,或者需要指出任何需要更正的地方,你可以通过CodeGuru论坛联系我,我的名字是Smasher/Devourer。Happy coding!
This article was originally published on July 11th, 2005
译者: 流星上的潴
再次感谢原文作者写出这么好的文章,也感谢译者翻译得不错!