自编码器 Tensorflow 实战 MNIST 数据集

1、生成模型

1.1、什么是生成模型

​ 概率统计层面：能够在给丁某一些隐含参数的条件下，随机生成观测数据的这样一种模型，称之为“生成模型”。它给观测值和比周数据系列制定一个连和概率分布

​ 机器学习层面：直接对数据进行建模，比如根据某个变量的概率密度函数进行数据采样。在贝叶斯算法中，直接对连和概率分布P(x,y)进行建模，然后利用贝叶斯公式进行求解P(y|x)。

1.2、生成模型分类

第一类：完全表示出数据确切的分布函数

第二类：没有办法完全表示出确切的分布函数，但是，能够做到的是新的数据的生成，而具体的分布函数是模糊的。

​ 在机器学习中，不管是自编码器AE、变分自编码器VAE、还是生成对抗网路GAN，都是属于第二类。生成新数据，也是大部分生成模型的核心目标。

2、自编码器原理

2.1、原理介绍

首先考虑监督学习中神经网络的功能：
$$o=f_{\theta }(x),x\in R^{d_{in}},o\in R^{d_{out}}$$
​ $d_{in}$ 是输入的特征向量长度，$d_{out}$ 是输出的特征向量长度。对于分类问题，网络模型通过把长度为 $d_{in}$ 输入特征向量变换到长度为$d_{out}$的输出向量，这个过程可以看成是特征降维的过程，把原始的高维输入向量变换到低维的变量。特征降维(Dimensionality Reduction)在机器学习中有广泛的应用，比如文件压缩(Compression)、数据预处理(Preprocessing)等。最常见的降维算法有主成分分析法(Principal components analysis，简称 PCA)，通过对协方差矩阵进行特征分解而得到数据的主要成分，但是 PCA 本质上是一种线性变换，提取特征的能力极为有限。

​ 那么能不能利用神经网络的强大非线性表达能力去学习到低维的数据表示呢？问题的关键在于，训练神经络一般需要一个显式的标签数据(或监督信号)，但是无监督的数据没有额外的标注信息，只有数据本身。

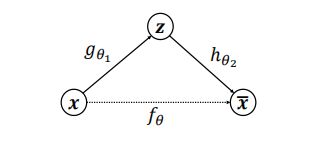
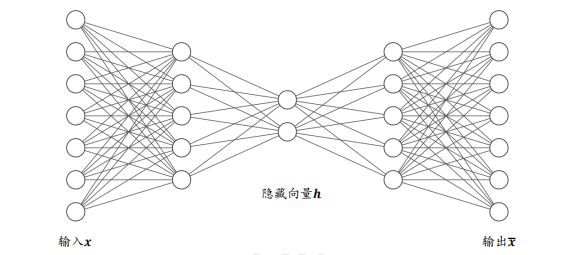
​ 所以，我们可以利用数据本身作为监督信号来进行网络训练，使得神经网络能够学习到映射$f_{\theta }:x\to x$。我们把网络$f_{\theta }$切分为两个部分，前面的子网络尝试学习映射关系:$g_{{\theta }_1}:x\to z$，后面的子网络尝试学习映射关系$h_{{\theta }_2}:z\to x$，如下图所示。我们把1看成一个数据编码(Encode)的过程，把高维度的输入编码成低维度的隐变量 (隐藏变量)，称为 Encoder 网络(编码器)；ℎ2看成数据解码(Decode)的过程，把编码过后的输入 解码为高维度的 ，称为 Decoder 网络(解码器)。

​ 编码器和解码器共同完成了输入数据的编码和解码过程，我们把整个网络模型 $g_{\theta }$ 叫做自动编码器(Auto-Encoder)，简称自编码器。如果使用深层神经网络来参数化和$g_{{\theta }_1}$ $h_{{\theta }_2}$ 函数，则 称为深度自编码器(Deep Auto-encoder)。

2.2、自编码器优化

自编码器能够将输入变换到隐藏向量 ，并通过解码器重建出 $\tilde{x}$。我们希望解码器的输出能够完美地或者近似恢复出原来的输入，即 $\tilde{x}\approx x$ ，那么，自编码器的优化目标可以写成：
$$\begin{gathered} MinimizeL=dist(x,\tilde{x}) \\ \tilde{x}=h_{{\theta }_2}(g_{{\theta }_1}(x)) \end{gathered}$$
其中 $dist(x,\tilde{x})$ 表示 和 $\tilde{x}$ 的距离度量，称为重建误差函数。最常见的度量方法有欧氏距离(Euclidean distance)的平方，计算方法如下：
$$L=\sum _i(x_i-\widetilde{x_i}{)}^2$$
自编码器网络和普通的神经网络并没有本质的区别，只不过训练的监督信号由标签变成了自身。借助于深层神经网络的非线性特征提取能力，自编码器可以获得良好的数据表示，相对于 PCA 等线性方法，自编码器性能更加优秀，甚至可以更加完美的恢复出输入。

3、自编码器实战 Fashion_MNIST

3.1、数据集介绍

Fashion_MNIST数据集是机器学习领域中非常经典的一个数据集，最简单的方法就是使用如下代码直接加载

import tensorflow as tf
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
print(X_train.shape, y_train.shape) 	#  (60000, 28, 28) (60000,)
print(X_test.shape, y_test.shape)		#  (10000, 28, 28) (10000,)

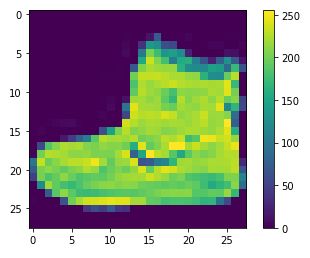
可以看出数据集由60000个训练样本和10000个测试样本组成，每个样本都是一张28 * 28像素的灰度图片，每个像素点是一个0-255的整数。

import matplotlib.pyplot as plt

plt.figure()
plt.imshow(X_train[0])
plt.colorbar()
plt.grid(False)
plt.show()

打印前25张图片

# 把像素值缩放到 0-1
X_train = X_train / 255.0
X_test = X_test / 255.0
# 所有的分类标签
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
               'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

plt.figure(figsize=(10,10))
for i in range(25):
    plt.subplot(5,5,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(X_train[i], cmap=plt.cm.binary)
    plt.xlabel(class_names[y_train[i]])

3.2 自编码器

构建自编码器神经网络

(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255.

train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(buffer_size=512).batch(512)
test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = test_db.batch(512)

class AutoEncoder(keras.Model):
    def __init__(self):
        super(AutoEncoder, self).__init__()
        # Encoders
        self.encoder = Sequential([
            layers.Dense(256, activation=tf.nn.relu),
            layers.Dense(128, activation=tf.nn.relu),
            layers.Dense(20)
        ])
        # Decoders
        self.decoder = Sequential([
            layers.Dense(128, activation=tf.nn.relu),
            layers.Dense(256, activation=tf.nn.relu),
            layers.Dense(784)
        ])
    # 前向计算
    def call(self, inputs, training=None):
        # [b, 784] => [b, 20]
        h = self.encoder(inputs)
        # [b, 20] => [b, 784]
        x_hat = self.decoder(h)
        return x_hat
# 创建自编码器对象
model = AutoEncoder()
model.build(input_shape=(None, 28 * 28))
# 配置 优化器
optimizer = tf.optimizers.Adam(learning_rate=1e-3)
# 开始训练
for epoch in range(20):
    for step, x in enumerate(train_db):
        #[b, 28, 28] => [b, 784]
        x = tf.reshape(x, [-1, 28 * 28])
        # 构建梯度记录器
        with tf.GradientTape() as tape:
            # 前向计算
            x_rec_logits = model(x)
            # 计算损失函数
            rec_loss = tf.losses.binary_crossentropy(x, x_rec_logits, from_logits=True)
            rec_loss = tf.reduce_mean(rec_loss)
        # 自动求导
        grads = tape.gradient(rec_loss, model.trainable_variables)
        # 更新网络
        optimizer.apply_gradients(zip(grads, model.trainable_variables))
    # 打印训练误差
    print("epoch: ", epoch, "loss: ", float(rec_loss))
    
# 打印查看生成的图片

x = next(iter(test_db))
logits = model(tf.reshape(x, [-1, 28 * 28]))
# 将输出值转化为像素值
x_hat = tf.sigmoid(logits)
# [b, 784] => [b, 28, 28] 恢复原始数据格式
x_hat = tf.reshape(x_hat, [-1, 28, 28])

# [b, 28, 28] => [2b, 28, 28]
# 输入的前 50 张+重建的前 50 张图片合并
x_concat = tf.concat([x[:50], x_hat[:50]], axis=0)
# 恢复为 0-255 的范围
x_concat = x_concat.numpy() * 255.
# 转换为整型
x_concat = x_concat.astype(np.uint8)
printImage(x_concat)
# 上 5 行是原图，下 5 行是使用主成分恢复的图

经过多次迭代，重建效果如下所示，其中上面5行是原图，下面5行是重建后的图片

​ 我们可以从图片中看出来，我们刚才上传给自编码模型的图片实质上是经过压缩以后再进行解压的一个过程。当压缩的时候，原有的图片的质量被缩减，解压的时候，用信息量小却包含了所有信息的文件来恢复出原来的图片。那么，为什么要这么做呢？当神经网络要输入大量的信息，比如高清图片的时候，输入的图像数量可以达到上千万，要神经网络直接从输入的数据量中进行学习，是一件非常费力不讨好的工作，因此我们就想，为什么不压缩一下呢？提取出原图片中最具有代表性的信息，缩减输入中的信息量，然后在把缩减过后的信息放入到神经网络中学习，这样学习起来就变得轻松了，所以自编码就是能在这个时候发挥作用。