语音信号处理基础(五)——语音分帧与加窗
文章目录
- 原理
- 1.加窗
- 2.分帧
一般而言语音处理的目的有两种:
一种是对语音信号进行分析,提取特征参数,用于后续处理;
提取的特征参数主要有语音的短时能量和平均幅度、短时平均过零率、短时自相关函数和短时平均幅度差函数等
另一种是加工语音信号,
例如在语音增强中对含噪语音进行背景噪声抑制,以获得相对“干净”的语音;在语音合成方中需要对分段语音进行拼接平滑,获得主观音质较高的合成语音,这方面的应用同样是建立在分析并提取语音信号信息的基础上的。总之,语音信号分析的目的就在于方便有效地提取并表示语音信号所携带的信息。
根据所分析的参数类型,语音信号分析可以分成时域分析和变换域(频域、倒谱域)分析。其中时域分析方法是最简单、最直观的方法,它直接对语音信号的时域波形进行分析,
提取的特征参数主要有语音的短时能量和平均幅度、短时平均过零率、短时自相关函数和短时平均幅度差函数等。
原理
不论是分析怎样的参数以及采用什么分析方法,在按帧进行语音分析、提取语音参数之前,有一些经常使用的、共同的短时分析技术必须预先进行,如语音信号的数字化、预加重、加窗和分帧等,这些也是不可忽视的语音信号分析的关键技术。
1.加窗
窗函数可以加在时域或频域上,更多的是加在时域上
常用的窗函数
1.矩形窗
w ( n ) = { 1 , 0 ⩽ n ⩽ N − 1 0 , 其 他 w(n)=\left\{\begin{array}{ll}{1,} & {0 \leqslant n \leqslant N-1} \\ {0,} & {其他}\end{array}\right. w(n)={1,0,0⩽n⩽N−1其他

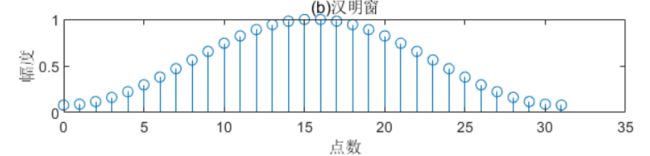
2.汉明窗
w ( n ) = { 0.54 − 0.46 cos [ 2 π n / ( N − 1 ) ] , 0 ⩽ n ⩽ N 0 , 其他 w(n)=\left\{\begin{array}{ll}{0.54-0.46 \cos [2 \pi n /(N-1)],} & {0 \leqslant n \leqslant N} \\ {0,} & {\text { 其他 }}\end{array}\right. w(n)={0.54−0.46cos[2πn/(N−1)],0,0⩽n⩽N 其他
 3.海宁窗
3.海宁窗
w ( n ) = { 0.5 ( 1 − cos [ 2 π n / ( N − 1 ) ] ) , 0 ⩽ n ⩽ N 0 , 其他 w(n)=\left\{\begin{array}{ll}{0.5(1-\cos [2 \pi n /(N-1)]),} & {0 \leqslant n \leqslant N} \\ {0,} & {\text { 其他 }}\end{array}\right. w(n)={0.5(1−cos[2πn/(N−1)]),0,0⩽n⩽N 其他

上述窗函数对应的幅频响应曲线为

注:矩形窗的主瓣宽度小于汉明窗,具有较高的频谱分辨率,但是矩形窗的旁瓣峰值较大,因此其频谱泄漏比较严重。
频谱泄漏( 对于频率为fs的正弦序列,它的频谱应该只是在fs处有离散谱。但是,在利用DFT求它的频谱时,对时域做了截断,结果使信号的频谱不只是在fs处有离散谱,而是在以fs为中心的频带范围内都有谱线出现,它们可以理解为是从fs频率上“泄漏”出去的,这种现象称 为频谱“泄漏”。 )
泄漏与窗函数频谱的两侧旁瓣有关,如果两侧旁瓣的高度趋于零,而使能量相对集中在主瓣,就可以较为接近于真实的频谱,为此,在时间域中可采用不同的窗函数来截断信号。
相比较,虽然汉明窗的主瓣宽度较宽,约大于矩形窗的一倍,但是它的旁瓣衰减较大,具有更平滑的低通特性,能够在较高的程度上反映短时信号的频率特性。
窗函数的选择(需要考虑其长度和形状)对短时分析参数的特性影响较大
所以选择合适的窗函数要考虑以下两个方面:
(1)窗口的形状
一个好的窗函数的标准是:在时域内语音波形乘以窗函数,要减小时间窗两端的坡度,使窗口边缘两端不引起急剧变化而平滑过渡到零,这样可以使截取出的语音波形缓慢降为零,减小语音帧的截断效应;在频域要有较宽的3dB带宽以及较小的边带最大值。
(2)窗口的长度
如果长度很大,则它等效于很窄的低通滤波器,语音信号通过时,反映波形细节的高频部分被阻碍,短时能量随时间变化很小,不能真实地反映语音信号的幅度变化:反之,长度太短时,滤波器的通带变宽,短时能量随时间有急剧的变化,不能得到平滑的能量函数。通常认为在一个语音帧内应包含1-7个基音周期。然而不同人的基音周期变化很大,从女性和儿童的2ms到老年男子的14 ms(即基音频率的变化范围为500-70 Hz),所以N的选择比较困难。通常在10kHz取样频率下,N折中选择为100-200点较合适(即 10-20 ms 持续时
三种窗函数的主瓣宽度B和第一旁瓣衰减A

△w是谱分析时的角频率分辨率。从表中可看出,矩形窗主瓣的宽度最窄,但第一旁瓣的衰减最小。也就是说,它的频谱泄漏要比另外两种窗函数大。在语音分析中,可根据不同的情况选择不同的窗函数。
2.分帧
贯穿于语音分析全过程的是“短时分析技术”
语音信号从整体来看其特性及表征其本质特征的参数均是随时间而变化的,所以它是一个非平稳态过程,不能用处理平稳信号的数字信号处理技术对其进行分析处理。但是,由于不同的语音是由人的口腔肌肉运动构成声道某种形状而产生的响应,而这种口腔肌肉运动相对于语音频率来说是非常缓慢的,所以从另一方面看,虽然语音信号具有时变特性,但在一个短时间范围内(认为在10-30 ms的短时间内),其特性基本保持不变即相对稳定,因而可以将其看作是一个准稳态过程,即语音信号具有短时平稳性。
所以任何语音信号的分析和处理必须建立在“短时”的基础上,即进行“短时分析”,将语音信号分为一段一段来分析其特征参数,其中每一段称为一“帧”,帧长一般即取为10-30 ms。
对于整体的语音信号而言,
分析出的是由每一帧特征参数组成的特征参数时间序列。
分帧示意图如图所示。(其中N为帧长,M为帧移)
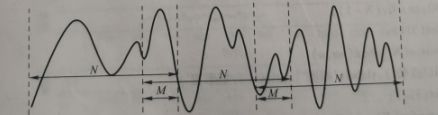
一般每秒的帧数约为33-100帧,视实际情况而定。分帧虽然可以采用连续分段的方法,但一般要采用交叠分段的方法,这是为了使帧与帧之间平滑过渡,保持其连续性。前一帧和后一帧的交叠部分称为帧移。帧移与帧长的比值一般取为0~1/2
语音信号的分帧是采用可移动的有限长度窗口进行加权的方法来实现的。
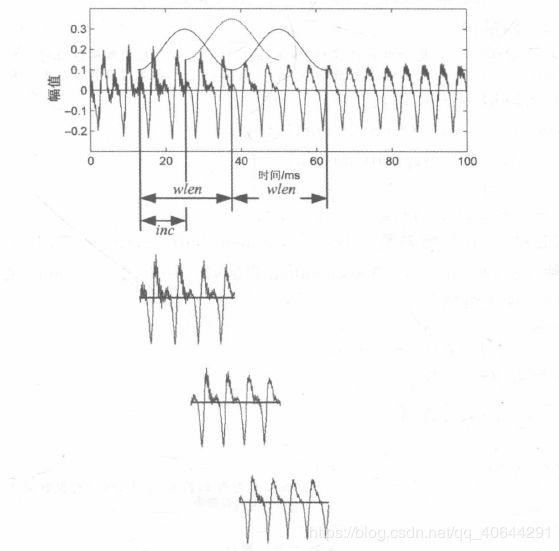
设读入语音文件的数据存放在y中,y长为N,采样频率为fs,,取每帧长为wlen。在上图中给出的语音段正发生在两个音节间过渡区,基音正发生着变化。如果相邻两帧不重叠(图中的两个用实线表示的窗),给出的基音可能有一个跳变。为了使其平稳过渡,在两帧之间再内插一帧或几帧,这样在相邻两帧之间就出现了重叠。后一帧对前一帧的位移量(简称为帧移)用inc表示,相邻两帧之间的重叠部分为overlap=wlen-inc。
对于长为N的语音信号分帧为
f n = ( N − overlap ) / i n c = ( N − w l e n + i n c ) / i n c = ( N − w l e n ) / i n c + 1 f n=(N-\text { overlap }) / i n c=(N-w l e n+i n c) / i n c \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad=(N-w l e n) / i n c+1 fn=(N− overlap )/inc=(N−wlen+inc)/inc=(N−wlen)/inc+1
这样就可以进行分帧了。设分帧后的数组为yseg,其中y是列数据序列
数据将被分为fn帧,每一帧在数据y中开始的位置为
indf=(0:(nf-1))*inc+1
而其中每一帧的数据位置为1至wlen,设成
inds=1:wlen
其中,indf是一个fn×1的列向量;inds是一个1×wlen的行向量。
扩展这两个向量:
indf(:,ones(1,wlen)); %把indf扩展成fn x wlen的矩阵,每一列的数值都和原indf一样
inds(ones(fn,1),:); %把inds扩展成fn × wlen的矩阵,每一行的数值都和原inds一样
这个过程可以用repmat函数:
indf(:,ones(1,wlen))→repmat(indf,1,wlen);
inds(ones(fn,1),:)→repmat(inds,fn,1);
所以分帧过程可写为
yseg=y(repmat(indf,1,wlen)+repmat(inds,fn,1));
MATLB中常用enframe和segment函数来分帧,都是这个原理
fix(x) 函数用来用法说明:y=fix(x) 函数将x中元素零方向取整,得到y是一个整数数组。对于复数z,分别对实部和虚部取整
分帧函数如下
%分帧函数
function frameout=enframe(x,win,inc)
nx=length(x(:)); % 取数据长度
nwin=length(win); % 取窗长
if (nwin == 1) % 判断窗长是否为1,若为1,即表示没有设窗函数
len = win; % 是,帧长=win
else
len = nwin; % 否,帧长=窗长
end
if (nargin < 3) % 如果只有两个参数,设帧inc=帧长
inc = len;
end
nf = fix((nx-len+inc)/inc); % 计算帧数
frameout=zeros(nf,len); % 初始化
indf= inc*(0:(nf-1)).'; % 设置每帧在x中的位移量位置
inds = (1:len); % 每帧数据对应1:len
frameout(:) = x(indf(:,ones(1,len))+inds(ones(nf,1),:)); % 对数据分帧
if (nwin > 1) % 若参数中包括窗函数,把每帧乘以窗函数
w = win(:)'; % 把win转成行数据
frameout = frameout .* w(ones(nf,1),:); % 乘窗函数
end
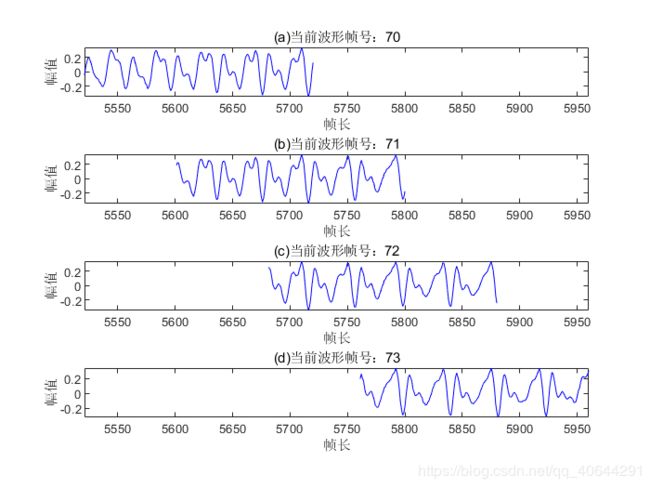
下面对一个语音信号进行分帧(不使用窗函数的情况),读取“我,到,北,京, 去”,选择起始帧号为70,显示出接下来的四帧
%语音分帧显示
%语音分帧显示
clc
clear all
[x,Fs]=audioread('C2_2_y.wav'); % 读入数据文件
wlen=200; inc=80; % 给出帧长和帧移
N=length(x); % 信号长度
time=(0:N-1)/Fs; % 计算出信号的时间刻度
signal=enframe(x,wlen,inc)'; % 分帧
i=input('请输入起始帧号(i):');
tlabel=i;
subplot 411;
% 画出第一帧时间波形
%tlabel-1)*inc+1:(tlabel-1)*inc+wlen 为起始帧第一帧的取值范围
plot((tlabel-1)*inc+1:(tlabel-1)*inc+wlen,signal(:,tlabel),'b');
%固定每一帧的长度
axis tight
xlim([(i-1)*inc+1 (i+2)*inc+wlen])
title(['(a)当前波形帧号:', num2str(i)]);
ylabel('幅值'); xlabel('帧长');
tlabel=i+1;
subplot 412;
% 画出第二帧时间波形
%(tlabel-1)*inc+1:(tlabel-1)*inc+wlen 为起始帧第二帧的取值范围
plot((tlabel-1)*inc+1:(tlabel-1)*inc+wlen,signal(:,tlabel),'b');
%固定每一帧的长度
axis tight
xlim([(i-1)*inc+1 (i+2)*inc+wlen])
title(['(b)当前波形帧号:', num2str(i+1)]);
ylabel('幅值'); xlabel('帧长');
tlabel=i+2;
subplot 413;
% 画出第三帧时间波形
plot((tlabel-1)*inc+1:(tlabel-1)*inc+wlen,signal(:,tlabel),'b');
%固定每一帧的长度
axis tight
xlim([(i-1)*inc+1 (i+2)*inc+wlen])
title(['(c)当前波形帧号:', num2str(i+2)]);
ylabel('幅值'); xlabel('帧长');
tlabel=i+3;
subplot 414;
% 画出第四帧时间波形
plot((tlabel-1)*inc+1:(tlabel-1)*inc+wlen,signal(:,tlabel),'b');
%固定每一帧的长度
axis tight
xlim([(i-1)*inc+1 (i+2)*inc+wlen])
title(['(d)当前波形帧号:', num2str(i+3)]);
ylabel('幅值'); xlabel('帧长');