关于java double类型运算的困惑

近期公司上线的会员项目中，发现有一处double计算后比较大小后没有正确返回true
导致错误的抛出了断言
经过DEBUG后发现，是因为double计算后精度丢失，出现浮点数导致

于是打开测试类进行测试:

public class Test {
    public static void main(String[] args) {
        double d = 0.05;
        double d2 = 0.01;
        System.out.println(d+d2);
    }
}

得到的结果如下:

0.060000000000000005

可以看到java在计算浮点数的时候,由于二进制无法精确表示0.1的值(就好比十进制无法精确表示1/3一样),所以一般会对小数格式化处理，但是如果涉及到金钱的项目,一点点误差都不能有,必须使用精确运算的时候,就可以使用BigDecimal方法计算.

查看了许多资料，终于找到原因

1.、内存结构

float和double的范围是由指数的位数来决定的。
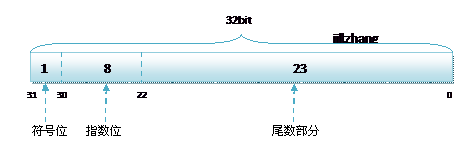
float的指数位有8位，而double的指数位有11位，分布如下：

image.png

loat：
1bit（符号位） 8bits（指数位） 23bits（尾数位）

image.png

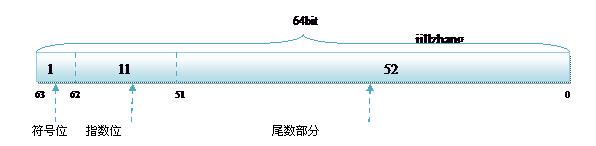
double：
1bit（符号位） 11bits（指数位） 52bits（尾数位）
于是，float的指数范围为-128 _{+127，而double的指数范围为-1024}+1023，并且指数位是按补码的形式来划分的。
其中负指数决定了浮点数所能表达的绝对值最小的非零数；而正指数决定了浮点数所能表达的绝对值最大的数，也即决定了浮点数的取值范围。
float的范围为-2^128 ~ +2^127，也即-3.40E+38 ~ +3.40E+38；double的范围为-2^1024 ~ +2^1023，也即-1.79E+308 ~ +1.79E+308。

2. 精度

float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。
float：2^23 = 8388608，一共七位，由于最左为1的一位省略了，这意味着最多能表示8位数： 28388608 = 16777216 。有8位有效数字，但绝对能保证的为7位，也即float的精度为7~8位有效数字；
double：2^52 = 4503599627370496，一共16位，同理，double的精度为16~17位*。

总结：

浮点运算很少是精确的，只要是超过精度能表示的范围就会产生误差。往往产生误差不是 因为数的大小，而是因为数的精度。因此，产生的结果接近但不等于想要的结果。尤其在使用 float 和 double 作精确运 算的时候要特别小心。
可以考虑采用一些替代方案来实现。如通过 String 结合 BigDecimal 或 者通过使用 long 类型来转换。

例:

import java.math.*;

public class BigDecimalDemo {
    public static void main(String[] args){
        System.out.println(ArithUtil.add(0.01, 0.05));
        System.out.println(ArithUtil.sub(1.0, 0.42));
        System.out.println(ArithUtil.mul(4.015, 100));
        System.out.println(ArithUtil.div(123.3, 100));
    }
}

class ArithUtil{
    private static final int DEF_DIV_SCALE=10;

    private ArithUtil(){}
    //相加
    public static double add(double d1,double d2){
        BigDecimal b1=new BigDecimal(Double.toString(d1));
        BigDecimal b2=new BigDecimal(Double.toString(d2));
        return b1.add(b2).doubleValue();

    }
    //相减
    public static double sub(double d1,double d2){
        BigDecimal b1=new BigDecimal(Double.toString(d1));
        BigDecimal b2=new BigDecimal(Double.toString(d2));
        return b1.subtract(b2).doubleValue();

    }
    //相乘
    public static double mul(double d1,double d2){
        BigDecimal b1=new BigDecimal(Double.toString(d1));
        BigDecimal b2=new BigDecimal(Double.toString(d2));
        return b1.multiply(b2).doubleValue();

    }
    //相除
    public static double div(double d1,double d2){

        return div(d1,d2,DEF_DIV_SCALE);

    }

    public static double div(double d1,double d2,int scale){
        if(scale<0){
            throw new IllegalArgumentException("The scale must be a positive integer or zero");
        }
        BigDecimal b1=new BigDecimal(Double.toString(d1));
        BigDecimal b2=new BigDecimal(Double.toString(d2));
        return b1.divide(b2,scale,BigDecimal.ROUND_HALF_UP).doubleValue();

    }

}