路径规划-bug算法

Bug1算法

如图2.1所示，起始点和目标点分别为qstart 和qgoal. 初始时刻 i = 0，令qL0 = qstart ，并称连接qLi 和 qgoal的线段为m-line. 没有遇到障碍时，机器人沿着m-line朝目标qgoal直线移动. 如果遇到障碍，则称点qH1为第一次遇到障碍时的撞击点（hit point）. 接着，机器人环绕障碍物移动直至返回 qH1点。然后判断出障碍物周边上离目标最近的点，并移到这个点上，该点称为离开点（leave point），由 qL1表示。从qL1开始机器人再次沿直线驶向目标，如果这条线与当前障碍物相交，则不存在到达目标的路径（如图2.2所示）。 Bug1算法的效率很低，但可以保证机器人能到达任何可达的目标。

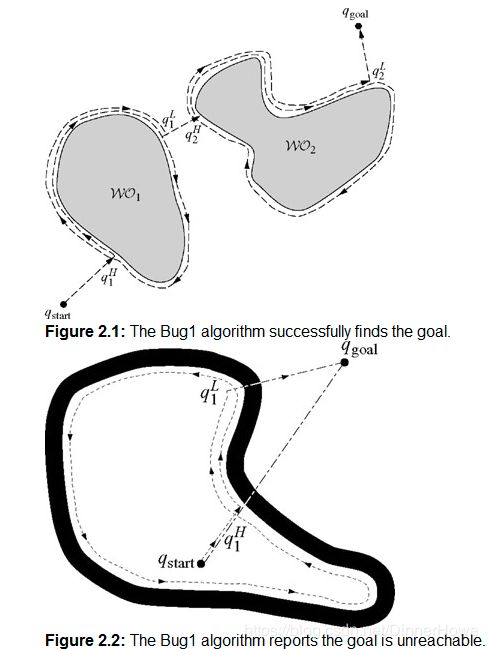
Bug2算法

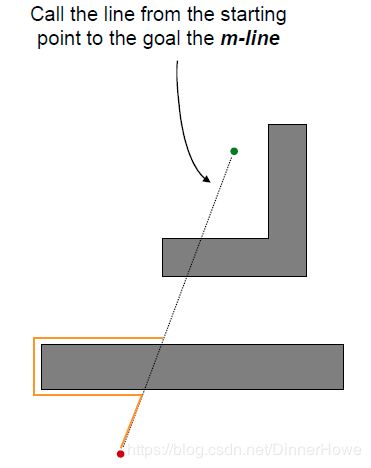
机器人先跟踪障碍物的轮廓，与Bug1不同的是，当它能直接移动到目标点时，就立即离开。如图2.3所示，Bug2算法中的m-line连接qstart和qgoal，为一条固定不变的直线。遇到障碍物时机器人会进入轮廓跟踪模式，当其到达m-line上一个接近目标点的位置后（而非初次遇到障碍物的撞击点），继续沿m-line驶向目标。如果机器人再次在m-line遇到上之前的撞击点，则到达目标的路径不存在（如图2.3中第二种情况所示）。

Bug2算法在一般情况下具有很短的移动路径，然而这种策略并非完美。如图2.4所示的螺旋形障碍物，其边界与m-line多次相交，我们可以根据上述Bug2算法的伪代码确定其运动路径：

1. qstart→qgoal，遇到障碍物，到达撞击点qH1；
2. qH1开始环绕障碍物，直到与m-line相交到达m点（此时进行判断：没有到达目标；没有再次遇到qH1；相比qH1点m点离目标更近；继续朝目标前进不会碰到障碍），则qL1=m，i=2。机器人从qL1沿着m-line继续朝目标前进；
3. 再次遇到障碍物，到达撞击点qH2，然后沿着障碍物边界移动，直到再次与m-line相交到达m点（此时进行判断：没有到达目标；没有再次遇到qH2；但继续朝目标前进会碰到障碍），由于不满足离开点的条件，则继续环绕；
4. 机器人环绕边界到达qH1点，与m-line相交（此时进行判断：没有到达目标；没有再次遇到qH2；但继续朝目标前进会碰到障碍），由于不满足离开点的条件，则继续环绕目标；
5. 机器人继续环绕边界到达qL1点，与m-line相交（此时进行判断：没有到达目标；没有再次遇到qH2；继续朝目标前进不会碰到障碍；但此时相比qH2机器人离目标位置更远），因此也不满足离开点条件，则继续环绕；
6. 机器人环绕边界，与m-line相交到达m点（此时进行判断：没有到达目标；没有再次遇到qH2；继续朝目标前进不会碰到障碍；但此时相比qH2机器人离目标位置更远），因此也不满足离开点条件，则继续环绕；
7. 机器人环绕边界，与m-line相交到达m点（此时进行判断：没有到达目标；没有再次遇到qH2；继续朝目标前进不会碰到障碍；相比qH2机器人离目标位置更近），满足离开点条件，则qL2=m，i=3;
8.机器人从qL2沿着m-line继续朝目标前进，到达目标位置。

Bug1 VS Bug2

• Bug1 is an exhaustive search algorithm——it looks at all choices before commiting

• Bug2 is a greedy algorithm—— it takes the first thing that looks better

• In many cases, Bug2 will outperform Bug1, but Bug1 has a more predictable performance overall

In fact, Bug1 and Bug2 illustrate two basic approaches to search problems. For each obstacle that it encounters, Bug1 performs an exhaustive search（穷举搜索） to find the optimal leave point. This requires that Bug1 traverse the entire perimeter of the obstacle, it is certain to have found the optimal leave point. In contrast, Bug2 uses an opportunistic（投机取巧的）approach. When Bug2 finds a leave point that is better than any it has seen before, it commits to that leave point. Such an algorithm is also called greedy, since it opts for the first promising option that is found. When the obstacles are simple, the greedy approach of Bug2 gives a quick payoff, but when the obstacles are complex, the more conservative approach of Bug1 often yields better performance. 即障碍物的“复杂度”越大的情况下，Bug1算法相比Bug2算法更有优势。

参考：

Principles of Robot Motion: Theory, Algorithms, and Implementation

Introduction to Autonomous Mobile Robots

http://www.leiphone.com/news/201605/tTC7DaH95LwnVIZW.html

http://www.codeproject.com/Articles/646347/Robotics-Motion-Planning-and-Navigation-Bug-Algori