LRU 和 LFU 缓存淘汰策略

• Redis 缓存淘汰策略
• 最近最久未使用算法（LRU）
  • 实现
  • LUR2
  • 其它扩展
• 最近最少使用算法（LFU）
  • 实现
  • 扩展
• 测试
• 参考

 

Redis 缓存淘汰策略

---

当缓存实际使用内存超过最大内存限制，将会执行内存淘汰。

Redis 提供以下六种内存淘汰策略：

• noeviction：禁止写入数据，允许继续读，保证已有的缓存数据不丢失。这是默认的淘汰策略。
• volatile-lru：从设置了过期时间的数据中，淘汰最近最久未使用的（LRU, Least Recently Used），保证无过期时间的数据不丢失。
• volatile-ttl：从设置了过期时间的数据中，淘汰过期时间 ttl 最近的。越快过期的优先淘汰。
• volatile-random：从设置了过期时间的数据中，随机淘汰。
• allkeys-lru：从所有数据中，淘汰最近最久未使用的（LRU）。
• allkeys-random：从所有数据中，随机淘汰。

按照淘汰数据的范围分，可以分为“停止写入”、“淘汰有过期时间的键”和“淘汰所有键”三个类别；

按照淘汰方式分，可以分为“淘汰最近最久未使用（LRU）”、“淘汰剩余寿命最短（ttl）”和“随机淘汰（random）”。

Redis 4.0 中新加入了两个基于 LFU（Least Frequently Used）的淘汰策略：

• volatile-lfu：从设置了过期时间的数据中，淘汰最近最少使用的。
• allkeys-lru：从所有数据中，淘汰最近最少使用的。

 

最近最久未使用算法（LRU）

---

实现

如果一个数据在最近一段时间没有被访问到，那么可以认为在将来它被访问的可能性也很小。因此，当空间满时，最久没有访问的数据最先被置换（淘汰）。

可以用哈希表（HashMap）和双向链表（LinkedList）共同实现 LRU 算法，链表中保存位置，哈希表用来存储和查找。在 JDK 中已经有对应的 LinkedHashMap。

LinkedHashMap 原理及源码解析详见 github。

/**
 * LRU
 * 

 * Retain latest accessed cache, eliminate the earliest accessed cache
 */
public class LRUCache<K, V> extends LinkedHashMap<K, V> {

    private final String name;
    private final Lock lock = new ReentrantLock();
    private volatile int maxCapacity;

    public LRUCache(String name) {
        this(name, Constants.CACHE_MAX_CAPACITY);
    }

    public LRUCache(String name, int maxCapacity) {
        super(16, Constants.DEFAULT_LOAD_FACTOR, true);
        this.name = name;
        this.maxCapacity = maxCapacity;
    }

    @Override
    protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) {
        return size() > maxCapacity;
    }

    @Override
    public boolean containsKey(Object key) {
        lock.lock();
        try {
            return super.containsKey(key);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public V get(Object key) {
        lock.lock();
        try {
            return super.get(key);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public V put(K key, V value) {
        lock.lock();
        try {
            return super.put(key, value);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public V remove(Object key) {
        lock.lock();
        try {
            return super.remove(key);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public int size() {
        lock.lock();
        try {
            return super.size();
        } finally {
            lock.unlock();
        }
    }

    @Override
    public void clear() {
        lock.lock();
        try {
            super.clear();
        } finally {
            lock.unlock();
        }
    }

    public int getMaxCapacity() {
        return maxCapacity;
    }

    public void setMaxCapacity(int maxCapacity) {
        this.maxCapacity = maxCapacity;
    }
}

---

LRU2

LRU-K

LRU-K 中的 K 代表最近使用的次数，因此 LRU 可以认为是 LRU-1。LRU-K 的主要目的是为了解决 LRU 算法“缓存污染”的问题，其核心思想是将“最近使用过 1 次”的判断标准扩展为“最近使用过 K 次”。

LRU-K 需要多维护一个队列，用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到 K 次的时候，才将数据放入缓存。下一次访问数据，同样先加入到历史队列，再次达到 K 次时，把它从历史队列删除，同时调整在缓存队列中的位置。也就是说，访问 K 次调整一次在缓存队列中的位置。

缓存中的数据遵循 LRU 的规则，即在需要淘汰时，选择第 K 次访问时间距当前时间最大的数据淘汰。

实际应用中 LRU-2 是综合各种因素后最优的选择，LRU-3 或者更大的 K 值命中率会高，但适应性差，需要大量的数据访问才能将历史访问记录清除掉。

下面借用 LinkedHashMap 实现 LRU2 算法。

/**
 * LRU-2
 * 

 * When the data accessed for the first time, add it to history list. If the size of history list reaches max capacity, eliminate the earliest data (first in first out).
 * When the data already exists in the history list, and be accessed for the second time, then it will be put into cache.
 */
public class LRU2Cache<K, V> extends LinkedHashMap<K, V> {

    private static final long serialVersionUID = -5167631809472116969L;

    private static final float DEFAULT_LOAD_FACTOR = 0.75f;

    private static final int DEFAULT_MAX_CAPACITY = 1000;
    private final Lock lock = new ReentrantLock();
    private volatile int maxCapacity;

    // as history list
    private PreCache<K, Boolean> preCache;

    public LRU2Cache() {
        this(DEFAULT_MAX_CAPACITY);
    }

    public LRU2Cache(int maxCapacity) {
        super(16, DEFAULT_LOAD_FACTOR, true);
        this.maxCapacity = maxCapacity;
        this.preCache = new PreCache<>(maxCapacity);
    }

    @Override
    protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) {
        return size() > maxCapacity;
    }

    @Override
    public boolean containsKey(Object key) {
        lock.lock();
        try {
            return super.containsKey(key);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public V get(Object key) {
        lock.lock();
        try {
            return super.get(key);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public V put(K key, V value) {
        lock.lock();
        try {
            if (preCache.containsKey(key)) {
                // add it to cache
                preCache.remove(key);
                return super.put(key, value);
            } else {
                // add it to history list
                preCache.put(key, true);
                return value;
            }
        } finally {
            lock.unlock();
        }
    }

    @Override
    public V remove(Object key) {
        lock.lock();
        try {
            preCache.remove(key);
            return super.remove(key);
        } finally {
            lock.unlock();
        }
    }

    @Override
    public int size() {
        lock.lock();
        try {
            return super.size();
        } finally {
            lock.unlock();
        }
    }

    @Override
    public void clear() {
        lock.lock();
        try {
            preCache.clear();
            super.clear();
        } finally {
            lock.unlock();
        }
    }

    public int getMaxCapacity() {
        return maxCapacity;
    }

    public void setMaxCapacity(int maxCapacity) {
        preCache.setMaxCapacity(maxCapacity);
        this.maxCapacity = maxCapacity;
    }


    static class PreCache<K, V> extends LinkedHashMap<K, V> {

        private volatile int maxCapacity;

        public PreCache() {
            this(DEFAULT_MAX_CAPACITY);
        }

        public PreCache(int maxCapacity) {
            super(16, DEFAULT_LOAD_FACTOR, true);
            this.maxCapacity = maxCapacity;
        }

        @Override
        protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) {
            return size() > maxCapacity;
        }

        public void setMaxCapacity(int maxCapacity) {
            this.maxCapacity = maxCapacity;
        }
    }
}

---

其它扩展

Two Queues(2Q)

2Q 算法使用两个队列，一个是 FIFO 队列，一个是 LRU 缓存队列。

数据第一次访问时将其加入到 FIFO 队列中，如果在 FIFO 队列中一直没有被访问则按 FIFO 的规则淘汰。第二次访问时将其移动到缓存队列中，在缓存中遵循 LRU 规则，按照 LRU 的方式淘汰。

Multi Queue(MQ)

2Q 使用两个队列，而 Multi Queue 在 2Q 的基础上，根据访问频率将数据划分为多个队列，不同的队列具有不同的访问优先级，其核心思想是：优先缓存访问次数多的数据。

但是 Multi Queue 需要维护多级队列，需要承受多级队列访问时间叠加的代价，虽然命中率较高，但是复杂度也很高。

 

最近最少使用算法（LFU）

---

实现

如果一个数据在最近一段时间很少被访问到，那么可以认为在将来它被访问的可能性也很小。因此，当空间满时，最小频率访问的数据最先被淘汰。

LFU 本质上是以访问频率为基础的 Top-K 算法，只需要直接淘汰访问频率最低的即可。

本文中 LFU 算法实现参考了 Leetcode460 - 哈希表 + 双向链表（Java）。

使用一个 HashMap 用于在 O(1) 时间内访问到缓存中的数据，另外使用一个 HashMap 保存访问次数和访问时间顺序，用于删除访问次数最小或时间最早的数据。前者的 key 是查找时数据的唯一标识，而 value 具体指的是 HitValue 实例，内部封装了访问次数、唯一标识、缓存数据。后者的 key 是访问次数，value 是 LinkedList 链表，链表顺序按照访问时间顺序排列，链表的节点保存的也是和前一个 Map 中同样的 HitValue 实例，所以不存在额外的空间浪费。链表按照访问时间顺序排列，如果记录了最小访问次数，可以在 O(1) 时间内找到需要淘汰的节点，然后删除它。

下图清晰地描述了该数据结构，同样引用自该博客：

更详细的解释请参考 Leetcode460 - 哈希表 + 双向链表（Java），下文中的代码由笔者自己实现，仅供参考：

public class LFUCache<K, V> {

    private final Lock lock = new ReentrantLock();
    private final int maxCapacity;
    private final Map<K, HitValue> cache;
    private final Map<Integer, LinkedList<HitValue>> frequency;
    private int minFrequency;

    public LFUCache(int maxCapacity) {
        this.maxCapacity = maxCapacity;
        this.cache = new HashMap<>();
        this.frequency = new HashMap<>();
        this.minFrequency = 1;
    }

    public void put(K key, V value) {
        lock.lock();
        try {
            if (cache.containsKey(key)) {
                // increment hit count of key, and move the HitValue to next bucket
                HitValue hitValue= addHitCount(key);
                // update the value of key
                hitValue.value = value;
                // update minFrequency
                updateMinFrequency(hitValue, Constants.LFU_UPDATE);
            } else {
                // check and eliminate
                removeEldest();
                // put new HitValue into cache
                HitValue hitValue = new HitValue(key, value, 1);
                cache.put(key, hitValue);
                if (!frequency.containsKey(1)) {
                    frequency.put(1, new LinkedList<>());
                }
                frequency.get(1).addLast(hitValue);
                // update minFrequency
                updateMinFrequency(hitValue, Constants.LFU_PUT);
            }

        } finally {
            lock.unlock();
        }
    }

    public V get(K key) {
        lock.lock();
        try {
            if (cache.containsKey(key)) {
                // increment hit count of key, and move the HitValue to next bucket
                HitValue hitValue = addHitCount(key);
                // update minFrequency
                updateMinFrequency(hitValue, Constants.LFU_GET);
                return hitValue.value;
            } else {
                return null;
            }
        } finally {
            lock.unlock();
        }
    }

    public V remove(K key) {
        lock.lock();
        try {
            if (cache.containsKey(key)) {
                // remove HitValue in cache or frequency
                HitValue hitValue = cache.remove(key);
                frequency.get(hitValue.hitCount).remove(hitValue);
                if (frequency.get(hitValue.hitCount).isEmpty()) {
                    frequency.remove(hitValue.hitCount);
                }
                // update minFrequency
                updateMinFrequency(null, Constants.LFU_REMOVE);
                return hitValue.value;
            } else {
                return null;
            }
        } finally {
            lock.unlock();
        }
    }

    public int size() {
        lock.lock();
        try {
            return cache.size();
        } finally {
            lock.unlock();
        }
    }

    public boolean containsKey(K key) {
        lock.lock();
        try {
            return cache.containsKey(key);
        } finally {
            lock.unlock();
        }
    }

    // addHitCount
    private HitValue addHitCount(K key) {
        HitValue hitValue = cache.get(key);
        int hitCount = hitValue.hitCount;
        hitValue.incr();
        LinkedList<HitValue> oldList = frequency.get(hitCount);
        oldList.remove(hitValue);
        if (frequency.get(hitCount).isEmpty()) {
            frequency.remove(hitCount);
        }
        if (!frequency.containsKey(hitCount + 1)) {
            frequency.put(hitCount + 1, new LinkedList<>());
        }
        LinkedList<HitValue> newList = frequency.get(hitCount + 1);
        newList.addLast(hitValue);
        return hitValue;
    }

    // eliminate
    private void removeEldest() {
        if (cache.size() >= maxCapacity) {
            LinkedList<HitValue> list = frequency.get(minFrequency);
            HitValue removedHitValue = list.removeFirst();
            if (list.isEmpty()) {
                frequency.remove(minFrequency);
            }
            cache.remove(removedHitValue.key);
        }
    }

    // update minFrequency
    // The “remove” mode should traverse the whole map to find the least
    // frequency hit count, it will take a lot of time. So try not to use "remove" method.
    private void updateMinFrequency(HitValue hitValue, String mode) {
        if (mode.equals(Constants.LFU_PUT)) {
            // put
            minFrequency = 1;
        } else if (mode.equals(Constants.LFU_REMOVE)) {
            // remove
            minFrequency = Collections.min(frequency.keySet());
        } else {
            // get,update
            if ((minFrequency == hitValue.hitCount - 1) &&
                    (!frequency.containsKey(hitValue.hitCount - 1)
                            || frequency.get(hitValue.hitCount - 1).isEmpty())) {
                minFrequency++;
            }
        }
    }

    // inner class which record hit value of cache
    private class HitValue{
        final K key;
        V value;
        int hitCount;

        HitValue(K key, V value, int hitCount) {
            this.key = key;
            this.value = value;
            this.hitCount = hitCount;
        }

        void incr() {
            this.hitCount++;
        }
    }
}

其中 Constants 类如下所示：

public class Constants {

	// ...

    // Cache
    public static final int CACHE_MAX_CAPACITY = 10000;
    public static final String LFU_PUT = "put";
    public static final String LFU_GET = "get";
    public static final String LFU_UPDATE = "update";
    public static final String LFU_REMOVE = "remove";

	// ...
}

LRU、LFU完整代码实现可见 github。

---

扩展

单纯的 LFU 算法在实际操作中可能会出现以下问题：

精确访问次数

如果某项数据的访问量非常大，导致访问次数太高，需要多余的空间来存储这个值，但实际上并不需要精确的访问次数。

解决方案：设置最高访问次数限制。也可以同时设置访问次数越高，递增的可能性越小。

“缓存泄漏”

访问次数很高的 key 可能之后不会再访问了，但是其访问次数过高一直占着内存不被淘汰。

解决方案：存储数据的最后访问时间，定时随机采样检查，如果距离现在已经超过了 N 秒钟，则访问次数递减或者减半。

此外，新加入的 key 访问次数太小，为了不被马上淘汰，可以适当增加初始值。

 

测试

---

对 LFU，LRU，LRU2 三种算法进行测试，测试程序如下：

public class CacheTest {
    public static void main(String[] args) {
        // 缓存区大小
        final int nCache = 100;
        // 数据量
        final int nNum = 100000;
        // 数据出现 1 次的比率-数据出现 2 次的比率-数据出现 4 次的比率-数据出现 8 次的比率-数据出现 100 次的比率
        final Ratio[] ratioSet = {
                new Ratio(0, 0, 0, 0, 100),
                new Ratio(10, 10, 10, 20, 50),
                new Ratio(20, 20, 20, 20, 20),
                new Ratio(50, 20, 10, 10, 10),
                new Ratio(70, 20, 10, 0, 0)
        };
        // 缓存策略
        LFUCache<Integer, Object> lfuCache = new LFUCache<>(nCache);
        LRUCache<Integer, Object> lruCache = new LRUCache<>(nCache);
        LRU2Cache<Integer, Object> lru2Cache = new LRU2Cache<>(nCache);
        // 开始测试
        for (Ratio ratio : ratioSet) {
            int[] data = test.getData(nNum, ratio);
            double lfuRate = test.hitRate(lfuCache, data);
            double lruRate = test.hitRate(lruCache, data);
            double lru2Rate = test.hitRate(lru2Cache, data);
            System.out.println("LFU-ratio-" + ratio.toString() + ": " + lfuRate);
            System.out.println("LRU-ratio-" + ratio.toString() + ": " + lruRate);
            System.out.println("LRU2-ratio-" + ratio.toString() + ": " + lru2Rate);
        }
    }

    public static CacheTest test = new CacheTest();

    private static final Map<String, Integer> RATIO_CONSTANT = new HashMap<>();
    static {
        RATIO_CONSTANT.put("OneRatio", 1);
        RATIO_CONSTANT.put("TwoRatio", 2);
        RATIO_CONSTANT.put("FourRatio", 4);
        RATIO_CONSTANT.put("EightRatio", 8);
        RATIO_CONSTANT.put("HundredRatio", 100);
    };
    private static final Class<Ratio> RATIO_CLASS = Ratio.class;
    private static final Random RANDOM = new Random();

    // 获取数据
    public int[] getData(int n, Ratio ratio) {
        int[] data = new int[n];
        int num = 1;
        Map<String, Integer> ratioMap = calculateRatioNum(n, ratio);
        for (Map.Entry<String, Integer> entry : ratioMap.entrySet()) {
            final int constant = RATIO_CONSTANT.get(entry.getKey());
            int constantT = constant;
            for (int i = 0; i < entry.getValue(); i++) {
                if (constantT == 0) {
                    num++;
                    constantT = constant;
                }
                int index = nextRandomIndex(n, data);
                data[index] = num;
                constantT--;
            }
        }
        return data;
    }

    // 命中率
    public double hitRate(Object cache, int[] data) {
        Object value = new Object();
        if (cache instanceof LFUCache) {
            LFUCache<Integer, Object> cacheT = (LFUCache<Integer,Object>) cache;
            int hits = 0;
            for (int k : data) {
                if (cacheT.containsKey(k))
                    hits++;
                cacheT.put(k, value);
            }
            return ((double) hits) / data.length;
        } else if (cache instanceof Map){
            Map<Integer, Object> cacheT = (Map<Integer, Object>) cache;
            int hits = 0;
            for (int k : data) {
                if (cacheT.containsKey(k))
                    hits++;
                cacheT.put(k, value);
            }
            return ((double) hits) / data.length;
        }
        return 0.0d;
    }

    private Map<String, Integer> calculateRatioNum(int n, Ratio ratio) {
        Map<String, Integer> ratioMap = new HashMap<>();
        for (String s : RATIO_CONSTANT.keySet()) {
            try {
                Method method = RATIO_CLASS.getMethod("get" + s);
                int num = (Integer)method.invoke(ratio) * n / 100;
                ratioMap.put(s, num);
            } catch (Exception e) {
                e.printStackTrace();
            }
        }
        return ratioMap;
    }

    private int nextRandomIndex(int n, int[] data) {
        int index = RANDOM.nextInt(n);
        while (data[index] != 0) {
            index = (index + 1 == n) ? 0 : index + 1;
        }
        return index;
    }
}

class Ratio {
    private int oneRatio;
    private int twoRatio;
    private int fourRatio;
    private int eightRatio;
    private int hundredRatio;

    public Ratio(int oneRate, int twoRate, int fourRatio, int eightRatio, int hundredRatio) {
        this.oneRatio = oneRate;
        this.twoRatio = twoRate;
        this.fourRatio = fourRatio;
        this.eightRatio = eightRatio;
        this.hundredRatio = hundredRatio;
    }

    public int getOneRatio() {
        return oneRatio;
    }

    public int getTwoRatio() {
        return twoRatio;
    }

    public int getFourRatio() {
        return fourRatio;
    }

    public int getEightRatio() {
        return eightRatio;
    }

    public int getHundredRatio() {
        return hundredRatio;
    }

    @Override
    public String toString() {
        return "[one-" + oneRatio + "-two-" + twoRatio + "-four-" + fourRatio + "-eight-" + eightRatio + "-hundred-" + hundredRatio + "]";
    }
}

使用 ratioSet 控制测试数据中重复数据的比率，也就是下面测试结果图中的横轴，测试数据量设置为 100000。

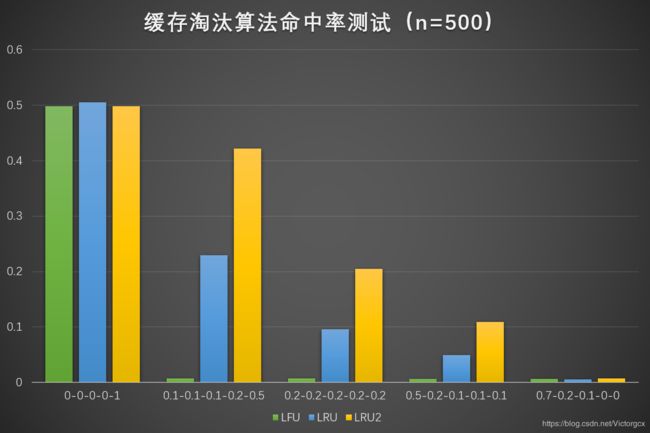
当缓存区大小为 500 时，结果如下所示：

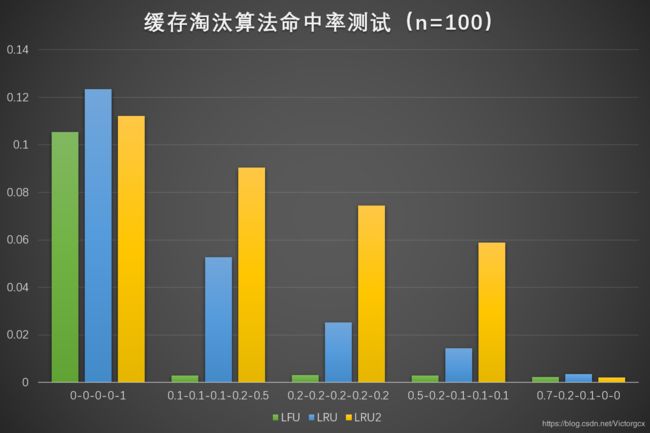
当缓存区大小为 100 时，结果如下所示：

当大量数据重复出现的时候，三种算法的效率都很高。

当重复数据量不断减少，特别是出现大量只出现一次就再也不会出现的“污染”数据时，LRU2 的性能比 LFU 和 LRU 好很多。

当污染数据占比过大时，三种算法的效率都很低。

总而言之，无论在哪种情况下，LRU2 都不会比 LRU 差，甚至在大多数情况下 LRU2 比 LRU 的命中率至少高出一倍以上。

完整测试程序可见 github。

 

参考

---

• 【Redis笔记】一起学习Redis | 聊聊Redis的内存淘汰LRU算法？
• 缓存算法（FIFO 、LRU、LFU三种算法的区别）
• Redis 4.0 新特性：LFU （update）
• LRU、LFU算法java实现
• LRU-K和2Q缓存算法介绍