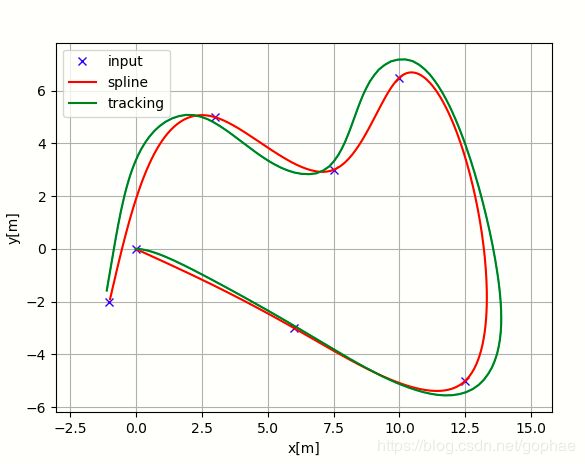
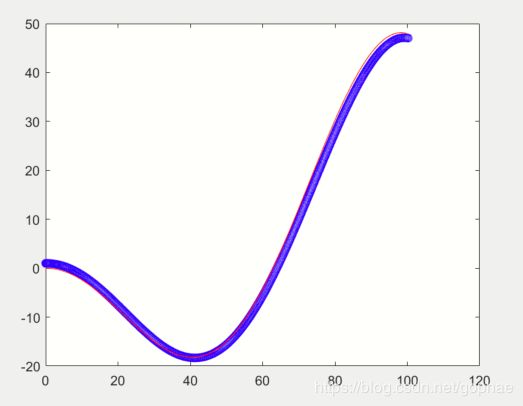
LQR轨迹跟踪算法Python/Matlab算法实现
Python:
"""
Path tracking simulation with LQR steering control and PID speed control.
author Atsushi Sakai (@Atsushi_twi)
"""
import sys
sys.path.append("H:\Project\TrajectoryPlanningModelDesign\Codes\frenet_optimal\frenet_optimal")
import cubic_spline
import numpy as np
import math
import matplotlib.pyplot as plt
import scipy.linalg as la
Kp = 1.0 # speed proportional gain
# LQR parameter
Q = np.eye(4)
R = np.eye(1)
# parameters
dt = 0.1 # time tick[s]
L = 0.5 # Wheel base of the vehicle [m]
max_steer = math.radians(45.0) # maximum steering angle[rad]
show_animation = True
# show_animation = False
class State:
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw
self.v = v
def update(state, a, delta):
if delta >= max_steer:
delta = max_steer
if delta <= - max_steer:
delta = - max_steer
state.x = state.x + state.v * math.cos(state.yaw) * dt
state.y = state.y + state.v * math.sin(state.yaw) * dt
state.yaw = state.yaw + state.v / L * math.tan(delta) * dt
state.v = state.v + a * dt
return state
def PIDControl(target, current):
a = Kp * (target - current)
return a
def pi_2_pi(angle): # the unit of angle is in rad;
while (angle > math.pi):
angle = angle - 2.0 * math.pi
while (angle < -math.pi):
angle = angle + 2.0 * math.pi
return angle
def solve_DARE(A, B, Q, R):
"""
solve a discrete time_Algebraic Riccati equation (DARE)
"""
X = Q
maxiter = 150
eps = 0.01
for i in range(maxiter):
Xn = A.T * X * A - A.T * X * B * \
la.inv(R + B.T * X * B) * B.T * X * A + Q
if (abs(Xn - X)).max() < eps:
X = Xn
break
X = Xn
return Xn
def dlqr(A, B, Q, R):
"""Solve the discrete time lqr controller.
x[k+1] = A x[k] + B u[k]
cost = sum x[k].T*Q*x[k] + u[k].T*R*u[k]
# ref Bertsekas, p.151
"""
# first, try to solve the ricatti equation
X = solve_DARE(A, B, Q, R)
# compute the LQR gain
K = np.matrix(la.inv(B.T * X * B + R) * (B.T * X * A))
eigVals, eigVecs = la.eig(A - B * K)
return K, X, eigVals
def lqr_steering_control(state, cx, cy, cyaw, ck, pe, pth_e):
ind, e = calc_nearest_index(state, cx, cy, cyaw)
k = ck[ind]
v = state.v
th_e = pi_2_pi(state.yaw - cyaw[ind])
A = np.matrix(np.zeros((4, 4)))
A[0, 0] = 1.0
A[0, 1] = dt
A[1, 2] = v
A[2, 2] = 1.0
A[2, 3] = dt
# print(A)
B = np.matrix(np.zeros((4, 1)))
B[3, 0] = v / L
K, _, _ = dlqr(A, B, Q, R)
x = np.matrix(np.zeros((4, 1)))
x[0, 0] = e
x[1, 0] = (e - pe) / dt
x[2, 0] = th_e
x[3, 0] = (th_e - pth_e) / dt
ff = math.atan2(L * k, 1)
fb = pi_2_pi((-K * x)[0, 0])
delta = 2*ff + 1 * fb
return delta, ind, e, th_e
def calc_nearest_index(state, cx, cy, cyaw):
dx = [state.x - icx for icx in cx]
dy = [state.y - icy for icy in cy]
d = [abs(math.sqrt(idx ** 2 + idy ** 2)) for (idx, idy) in zip(dx, dy)]
mind = min(d)
ind = d.index(mind)
dxl = cx[ind] - state.x
dyl = cy[ind] - state.y
angle = pi_2_pi(cyaw[ind] - math.atan2(dyl, dxl))
if angle < 0:
mind *= -1
return ind, mind
def closed_loop_prediction(cx, cy, cyaw, ck, speed_profile, goal):
T = 500.0 # max simulation time
goal_dis = 0.3
stop_speed = 0.05
state = State(x=-0.0, y=-0.0, yaw=0.0, v=0.0)
time = 0.0
x = [state.x]
y = [state.y]
yaw = [state.yaw]
v = [state.v]
t = [0.0]
target_ind = calc_nearest_index(state, cx, cy, cyaw)
e, e_th = 0.0, 0.0
while T >= time:
dl, target_ind, e, e_th = lqr_steering_control(
state, cx, cy, cyaw, ck, e, e_th)
ai = PIDControl(speed_profile[target_ind], state.v)
state = update(state, ai, dl)
if abs(state.v) <= stop_speed:
target_ind += 1
time = time + dt
# check goal
dx = state.x - goal[0]
dy = state.y - goal[1]
if math.sqrt(dx ** 2 + dy ** 2) <= goal_dis:
print("Goal")
break
x.append(state.x)
y.append(state.y)
yaw.append(state.yaw)
v.append(state.v)
t.append(time)
if target_ind % 1 == 0 and show_animation:
plt.cla()
plt.plot(cx, cy, "-r", label="course")
plt.plot(x, y, "ob", label="trajectory")
plt.plot(cx[target_ind], cy[target_ind], "xg", label="target")
plt.axis("equal")
plt.grid(True)
plt.title("speed[km/h]:" + str(round(state.v * 3.6, 2)) +
",target index:" + str(target_ind))
plt.pause(0.0001)
return t, x, y, yaw, v
def calc_speed_profile(cx, cy, cyaw, target_speed):
speed_profile = [target_speed] * len(cx)
direction = 1.0
# Set stop point
for i in range(len(cx) - 1):
dyaw = abs(cyaw[i + 1] - cyaw[i])
switch = math.pi / 4.0 <= dyaw < math.pi / 2.0
if switch:
direction *= -1
if direction != 1.0:
speed_profile[i] = - target_speed
else:
speed_profile[i] = target_speed
if switch:
speed_profile[i] = 0.0
speed_profile[-1] = 0.0
# flg, ax = plt.subplots(1)
# plt.plot(speed_profile, "-r")
# plt.show()
return speed_profile
def main():
print("LQR steering control tracking start!!")
ax = [0.0, 6.0, 12.5, 10.0, 7.5, 3.0, -1.0]
ay = [0.0, -3.0, -5.0, 6.5, 3.0, 5.0, -2.0]
goal = [ax[-1], ay[-1]]
cx, cy, cyaw, ck, s = cubic_spline.calc_spline_course(
ax, ay, ds=0.1)
target_speed = 10.0 / 3.6 # simulation parameter km/h -> m/s
sp = calc_speed_profile(cx, cy, cyaw, target_speed)
t, x, y, yaw, v = closed_loop_prediction(cx, cy, cyaw, ck, sp, goal)
if show_animation:
plt.close()
flg, _ = plt.subplots(1)
plt.plot(ax, ay, "xb", label="input")
plt.plot(cx, cy, "-r", label="spline")
plt.plot(x, y, "-g", label="tracking")
plt.grid(True)
plt.axis("equal")
plt.xlabel("x[m]")
plt.ylabel("y[m]")
plt.legend()
flg, ax = plt.subplots(1)
plt.plot(s, [math.degrees(iyaw) for iyaw in cyaw], "-r", label="yaw")
plt.grid(True)
plt.legend()
plt.xlabel("line length[m]")
plt.ylabel("yaw angle[deg]")
flg, ax = plt.subplots(1)
plt.plot(s, ck, "-r", label="curvature")
plt.grid(True)
plt.legend()
plt.xlabel("line length[m]")
plt.ylabel("curvature [1/m]")
plt.show()
if __name__ == '__main__':
main()
然后还要把cubic spline放在同一个project下进行调用, 注意修改路径,我的路径是:
sys.path.append("H:\Project\TrajectoryPlanningModelDesign\Codes\python\tracking_pure_stan")
#自己把它修改成你的路径。然后系统就可以调用了。
#下面就是cubic spline的class,
import math
import numpy as np
import bisect
class Spline:
u"""
Cubic Spline class
"""
def __init__(self, x, y):
self.b, self.c, self.d, self.w = [], [], [], []
self.x = x
self.y = y
self.nx = len(x) # dimension of x
h = np.diff(x)
# calc coefficient c
self.a = [iy for iy in y]
# calc coefficient c
A = self.__calc_A(h)
B = self.__calc_B(h)
self.c = np.linalg.solve(A, B)
# print(self.c1)
# calc spline coefficient b and d
for i in range(self.nx - 1):
self.d.append((self.c[i + 1] - self.c[i]) / (3.0 * h[i]))
tb = (self.a[i + 1] - self.a[i]) / h[i] - h[i] * \
(self.c[i + 1] + 2.0 * self.c[i]) / 3.0
self.b.append(tb)
def calc(self, t):
u"""
Calc position
if t is outside of the input x, return None
"""
if t < self.x[0]:
return None
elif t > self.x[-1]:
return None
i = self.__search_index(t)
dx = t - self.x[i]
result = self.a[i] + self.b[i] * dx + \
self.c[i] * dx ** 2.0 + self.d[i] * dx ** 3.0
return result
def calcd(self, t):
u"""
Calc first derivative
if t is outside of the input x, return None
"""
if t < self.x[0]:
return None
elif t > self.x[-1]:
return None
i = self.__search_index(t)
dx = t - self.x[i]
result = self.b[i] + 2.0 * self.c[i] * dx + 3.0 * self.d[i] * dx ** 2.0
return result
def calcdd(self, t):
u"""
Calc second derivative
"""
if t < self.x[0]:
return None
elif t > self.x[-1]:
return None
i = self.__search_index(t)
dx = t - self.x[i]
result = 2.0 * self.c[i] + 6.0 * self.d[i] * dx
return result
def __search_index(self, x):
u"""
search data segment index
"""
return bisect.bisect(self.x, x) - 1
def __calc_A(self, h):
u"""
calc matrix A for spline coefficient c
"""
A = np.zeros((self.nx, self.nx))
A[0, 0] = 1.0
for i in range(self.nx - 1):
if i != (self.nx - 2):
A[i + 1, i + 1] = 2.0 * (h[i] + h[i + 1])
A[i + 1, i] = h[i]
A[i, i + 1] = h[i]
A[0, 1] = 0.0
A[self.nx - 1, self.nx - 2] = 0.0
A[self.nx - 1, self.nx - 1] = 1.0
# print(A)
return A
def __calc_B(self, h):
u"""
calc matrix B for spline coefficient c
"""
B = np.zeros(self.nx)
for i in range(self.nx - 2):
B[i + 1] = 3.0 * (self.a[i + 2] - self.a[i + 1]) / \
h[i + 1] - 3.0 * (self.a[i + 1] - self.a[i]) / h[i]
# print(B)
return B
class Spline2D:
u"""
2D Cubic Spline class
"""
def __init__(self, x, y):
self.s = self.__calc_s(x, y)
self.sx = Spline(self.s, x)
self.sy = Spline(self.s, y)
def __calc_s(self, x, y):
dx = np.diff(x)
dy = np.diff(y)
self.ds = [math.sqrt(idx ** 2 + idy ** 2)
for (idx, idy) in zip(dx, dy)]
s = [0]
s.extend(np.cumsum(self.ds))
return s
def calc_position(self, s):
u"""
calc position
"""
x = self.sx.calc(s)
y = self.sy.calc(s)
return x, y
def calc_curvature(self, s):
u"""
calc curvature
"""
dx = self.sx.calcd(s)
ddx = self.sx.calcdd(s)
dy = self.sy.calcd(s)
ddy = self.sy.calcdd(s)
k = (ddy * dx - ddx * dy) / (dx ** 2 + dy ** 2)
return k
def calc_yaw(self, s):
u"""
calc yaw
"""
dx = self.sx.calcd(s)
dy = self.sy.calcd(s)
yaw = math.atan2(dy, dx)
return yaw
def calc_spline_course(x, y, ds=0.1):
sp = Spline2D(x, y)
s = list(np.arange(0, sp.s[-1], ds))
rx, ry, ryaw, rk = [], [], [], []
for i_s in s:
ix, iy = sp.calc_position(i_s)
rx.append(ix)
ry.append(iy)
ryaw.append(sp.calc_yaw(i_s))
rk.append(sp.calc_curvature(i_s))
return rx, ry, ryaw, rk, s
Matlab
clc
clear all
Kp = 1.0 ;
dt = 0.1 ;% [s]
L = 2.9 ;% [m] wheel base of vehicle
Q = eye(4);
R = eye(1);
max_steer =60 * pi/180; % in rad
target_speed = 15.0 / 3.6;
cx = 0:0.1:200; % sampling interception from 0 to 100, with step 0.1
for i = 1:500% here we create a original reference line, which the vehicle should always follow when there is no obstacles;
cy(i) = -sin(cx(i)/20)*cx(i)/2;
end
for i = 501: length(cx)
cy(i) = -sin(cx(i)/20)*cx(i)/2; %cy(500);
end
p = [cx', cy'];
for i = 1:length(cx)-1
pd(i) = (p(i+1,2)-p(i,2))/(p(i+1,1)-p(i,1));
end
pd(end+1) = pd(end);
%计算一阶导数
for i =2: length(cx)-1
pdd(i) = (p(i+1,2)-2*p(i,2) + p(i-1,2))/(0.5*(-p(i-1,1)+p(i+1,1)))^2;
end
pdd(1) = pdd(2);
pdd(length(cx)) = pdd(length(cx)-1);
for i = 1:length(cx)
k(i) = (pdd(i))/(1+pd(i)^2)^(1.5);
end
cx= cx'
cy =cy'
cyaw = atan(pd');
ck = k'
% plot(1:1001, cyaw)
% plot(1:1001, ck)
% plot(1:1001, pd)
pe = 0; pth_e = 0;
i = 1;
target_v = 10/3.6;
T = 80;
lastIndex = length(cx);
x = 0; y = -1; yaw = 0; v = 0;
time = 0;
ind =0;
figure
while ind < length(cx)
[delta,ind,e,th_e] = lqr_steering_control(x,y,v,yaw,cx,cy,cyaw,ck, pe, pth_e,L,Q,R,dt);
pe =e;
pth_e = th_e;
if abs(e)> 4
fprintf('mayday mayday!\n')
break;
end
delta
a = PIDcontrol(target_v, v, Kp);
[x,y,yaw,v] = update(x,y,yaw,v, a, delta, dt,L, max_steer);
posx(i) = x;
posy(i) =y;
i = i+1;
plot(cx,cy,'r-')
hold on
plot(posx(i-1),posy(i-1),'bo')
drawnow
hold on
end
% function"Update" updates vehicle states
function [x, y, yaw, v] = update(x, y, yaw, v, a, delta,dt,L,max_steer)
delta = max(min(max_steer, delta), -max_steer);
x = x + v * cos(yaw) * dt;
y = y + v * sin(yaw) * dt;
yaw = yaw + v / L * tan(delta) * dt;
v = v + a * dt;
end
function [a] = PIDcontrol(target_v, current_v, Kp)
a = Kp * (target_v - current_v);
end
function [angle] = pipi(angle) % the unit of angle is in rad;
if (angle > pi)
angle = angle - 2*pi;
elseif (angle < -pi)
angle = angle + 2*pi;
else
angle = angle;
end
end
function [Xn] = solve_DARE(A,B,Q,R)
X = Q;
maxiter = 150;
epsilon = 0.01;
for i = 1:maxiter
Xn = A' * X * A - A' * X * B * ((R + B' * X * B) \ B') * X * A +Q;
if abs(Xn - X) <= epsilon
X = Xn;
break;
end
X = Xn;
end
end
function [K] = dlqr (A,B,Q,R)
X = solve_DARE(A,B,Q,R);
K = (B' * X * B + R) \ (B' * X * A);
end
function [delta,ind,e,th_e] = lqr_steering_control(x,y,v,yaw,cx,cy,cyaw,ck, pe, pth_e,L,Q,R,dt)
[ind, e] = calc_target_index(x,y,cx,cy,cyaw);
k =ck(ind);
th_e = pipi(yaw -cyaw(ind));
A = zeros(4,4);
A(1,1) = 1; A(1,2) = dt; A(2,3) = v; A(3,3) = 1; A(3,4) = dt;
B= zeros(4,1);
B(4,1) = v/L;
K = dlqr(A,B,Q,R);
x = zeros(4,1);
x(1,1)=e; x(2,1)= (e-pe)/dt; x(3,1) = th_e; x(4,1) = (th_e - pth_e)/dt;
ff = atan(L * (k));
fb = pipi(-K * x);
delta = 1*ff + 1*fb;
ff
fb
end
function [ind, error] = calc_target_index(x,y, cx,cy,cyaw)
N = length(cx);
Distance = zeros(N,1);
for i = 1:N
Distance(i) = sqrt((cx(i)-x)^2 + (cy(i)-y)^2);
end
[value, location]= min(Distance);
ind = location
dx1 = cx(ind)- x;
dy1 = cy(ind) -y;
angle = pipi(cyaw(ind)-atan(dy1/dx1));
heading = cyaw(ind)*180/pi
if y<cy(ind)
error = -value;
else
error = value;
end
end
% if cx(ind)> x
% error = -value;
% else
% error = value;
% end