机器学习：线性回归（Linear Regression）小项目

该小项目所有代码在我的github上，欢迎有兴趣的同学与我探讨研究～
地址：Machine-Learning/machine-learning-ex1/

---

1. Introduction

线性回归(Linear Regression)，在wiki上的定义如下：

In statistics, linear regression is a linear approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression.

谈谈我个人的理解吧。
线性回归，从应用层面上来讲，是用于数据拟合的工具。从许多数据中找到一条直线能够拟合大部分数据，从而能够根据输入的值预测输出的值。

何为线性？数据拟合得到的是呈线性的，换句话说就是条直线。
何为回归？就是根据以前的数据预测出一个准确的输出值。

而线性回归算法，可以分为两类：

• Linear Regression with one variable 单变量线性回归
• Linear Regression with multiple variable 多变量线性回归
  注：有时会用feature代替variable这个词

而解决线性回归问题，通常会涉及到两种方法：

• Gradient Descent 梯度下降法
• Normal Equation 正规方程法

简单谈谈什么时候使用梯度下降法，什么时候使用正规方程法？

• 首先，正规方程法在训练集个数较少时(<10000)，计算效率会优于梯度下降法，否则便使用梯度下降法；
• 其次，正规方程法不需要设定学习率，即不会涉及到调参的问题，且不需要迭代；

• 最后，梯度下降法的时间复杂度O(kn^2), 正规方程法的时间复杂度O(n^3)。

  总而言之，训练集个数少于10000优先使用正规方程法，否则使用梯度下降法。

对于多变量的线性回归，还会涉及到：

• Feature scaling 特征缩放
• Mean Normalization 均值归一化
  注：有时会提到Feature Normalization，指的便是Mean Normalization。

还有，Vectorization(向量化)：
很多复杂的计算都可以转换成矩阵或者向量的计算，这在一定程度上大大提高了计算的效率。同时，代码也会变的十分简洁。待会在项目代码中会有所体现。

最后，还得了解一下Cost Function (损失／代价函数)。当数据拟合度越高，损失函数的值越小，极限是等于0.

需要掌握的公式：
1. 线性回归函数(含一般式与向量式)；
2. 损失函数；
3. 梯度下降的迭代式子(含一般式和向量式)；
4. 正规函数参数向量化求法。

声明：本项目代码用Octave实现(语法与matlab相似)。 代码注释很详细，就不另外讲解了了～

2. Linear Regression with one variable

主函数：

%% Initialization
% clear means clear all the valuable in the workspace
% close all means close all the windows except the main window
% clc means clean all the info in command 
clear ; close all; clc

%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()

fprintf('Program paused. Press enter to continue.\n');
pause;


%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples

% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);

fprintf('Program paused. Press enter to continue.\n');
pause;

%% =================== Part 3: Cost and Gradient descent ===================

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters

% Some gradient descent settings
iterations = 1500;
alpha = 0.01;

fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');

% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');

fprintf('Program paused. Press enter to continue.\n');
pause;

fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);

% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n  1.1664\n\n');

% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure

% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
    predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
    predict2*10000);

fprintf('Program paused. Press enter to continue.\n');
pause;

%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')

% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);

% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));

% Fill out J_vals
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
      t = [theta0_vals(i); theta1_vals(j)];
      J_vals(i,j) = computeCost(X, y, t);
    end
end


% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');

% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

Part1纯属打酱油，跳过。

Part2，构图，显示训练集中待拟合的数据。
plotData.m

function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure 
%   PLOTDATA(x,y) plots the data points and gives the figure axes labels of
%   population and profit.

figure; % open a new figure window

% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the 
%               "figure" and "plot" commands. Set the axes labels using
%               the "xlabel" and "ylabel" commands. Assume the 
%               population and revenue data have been passed in
%               as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
%       appear as red crosses. Furthermore, you can make the
%       markers larger by using plot(..., 'rx', 'MarkerSize', 10);
    plot(x, y, 'rx');
    xlabel("population");
    ylabel("profit");
% ============================================================

end

上图中的小红叉代表训练集中的training example。

Part3:求代价函数，梯度下降，构图显示拟合的直线
computeCost.m

function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.

% 得到括号内的值
A = X*theta-y;
% 再将括号平方
A = A.^2;
% 得到求和的值
errorSum = sum(A);
% 得到损失函数
J = 1/(2*m)*errorSum;

% =========================================================================

end

gradientDescent.m

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    % 得到求和的值
    sum = ((X*theta-y)'*X)';
    % 得到偏导的值
    derivative = 1/m*sum;
    % 得到迭代后的theta
    theta = theta - alpha*derivative;
    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end

end

Part4: 画出损失函数的图像以及theta的轮廓图。

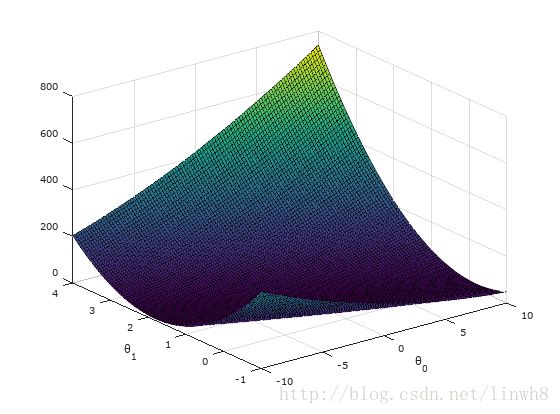
损失函数的弓形图

theta的轮廓图，小红叉接近中央。

终端输出：

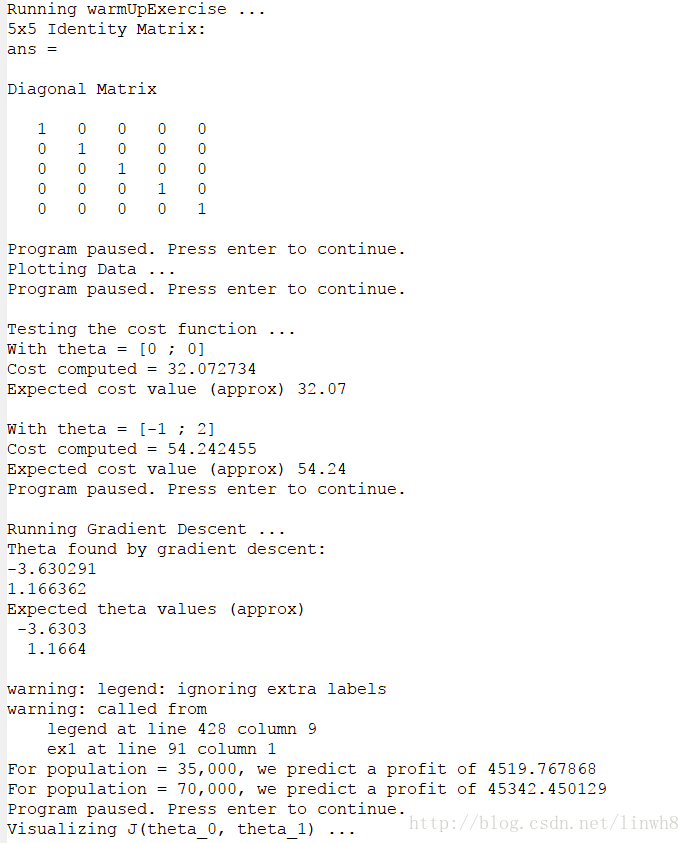
从输出可以看到，梯度下降得到的结果与预期十分接近。

3. Linear Regression with multiple variable

主函数：

%% Initialization

%% ================ Part 1: Feature Normalization ================

%% Clear and Close Figures
clear ; close all; clc

fprintf('Loading data ...\n');

%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);

% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');

fprintf('Program paused. Press enter to continue.\n');
pause;

% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');

[X mu sigma] = featureNormalize(X);

% Add intercept term to X
X = [ones(m, 1) X];


%% ================ Part 2: Gradient Descent ================

% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
%               code that runs gradient descent with a particular
%               learning rate (alpha). 
%
%               Your task is to first make sure that your functions - 
%               computeCost and gradientDescent already work with 
%               this starter code and support multiple variables.
%
%               After that, try running gradient descent with 
%               different values of alpha and see which one gives
%               you the best result.
%
%               Finally, you should complete the code at the end
%               to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
%       graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%

fprintf('Running gradient descent ...\n');

% Choose some alpha value
alpha = 0.01;
num_iters = 400;

% Init Theta and Run Gradient Descent 
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);

% Plot the convergence graph
% numel() ·µ»ØÔªËظöÊý    
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');

% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');

% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = 0; % You should change this
price = [1, 1650, 3]*theta;

% ============================================================

fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
         '(using gradient descent):\n $%f\n'], price);

fprintf('Program paused. Press enter to continue.\n');
pause;

%% ================ Part 3: Normal Equations ================

fprintf('Solving with normal equations...\n');

% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form 
%               solution for linear regression using the normal
%               equations. You should complete the code in 
%               normalEqn.m
%
%               After doing so, you should complete this code 
%               to predict the price of a 1650 sq-ft, 3 br house.
%

%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);

% Add intercept term to X
X = [ones(m, 1) X];

% Calculate the parameters from the normal equation
theta = normalEqn(X, y);

% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');


% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = 0; % You should change this
price = [1, 1650, 3]*theta;

% ============================================================

fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
         '(using normal equations):\n $%f\n'], price);

Part1： 特征归一化 (特征-特征对应的均值)／(特征对应的标准差或者max-min)
featureNormalize.m

function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X 
%   FEATURENORMALIZE(X) returns a normalized version of X where
%   the mean value of each feature is 0 and the standard deviation
%   is 1. This is often a good preprocessing step to do when
%   working with learning algorithms.

% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));

% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
%               of the feature and subtract it from the dataset,
%               storing the mean value in mu. Next, compute the 
%               standard deviation of each feature and divide
%               each feature by it's standard deviation, storing
%               the standard deviation in sigma. 
%
%               Note that X is a matrix where each column is a 
%               feature and each row is an example. You need 
%               to perform the normalization separately for 
%               each feature. 
%
% Hint: You might find the 'mean' and 'std' functions useful.
%       

% 求特征对应均值
  mu = mean(X);
% 求特征对应标准差
  sigma = std(X);
% 特征均一化，即特征减去均值除以标准差(或者max-min)
% 易错
% 错误写法： x_norm = (X-mu) ./ sigma;

X_norm = (X - ones(length(X), 1) * mu) ./ (ones(length(X), 1) * sigma);

% ============================================================

end

这里有小坑：

错误写法： x_norm = (X-mu) ./ sigma;
正确写法：X_norm = (X - ones(length(X), 1) * mu) ./ (ones(length(X), 1) * sigma);

必须将mu转化为与X同规格的矩阵，sigma也是。
如果你单单只是计算X-mu，或者X .／sigma，是没有问题的，octave会自动给你修复填充，将mu与sigma变成与X同规格的矩阵。可是如果你直接把他们揉杂在一起，就像我上面的错误写法，则octave不会自动给你修复填充，所以会出现theta是NAN的情况。

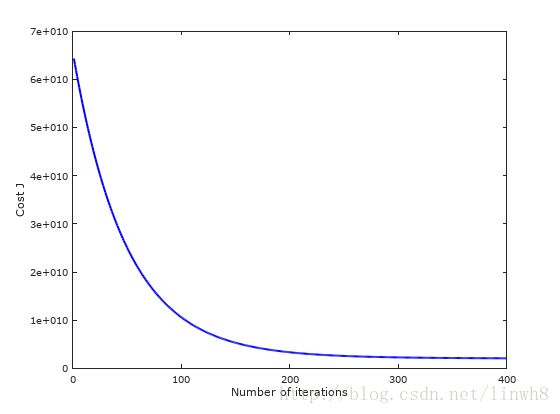
Part2: 梯度下降，同时画出损失函数的值随着迭代次数的变化图像，以确保梯度下降能正常执行。

梯度下降的代码与前面的一致。

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    sum = ((X*theta-y)'*X)';
    derivative = 1/m*sum;
    theta = theta - alpha*derivative;
    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end

end

下降速度适中，梯度下降正常运行。
Part3: 正规方程解法

function [theta] = normalEqn(X, y)
%NORMALEQN Computes the closed-form solution to linear regression 
%   NORMALEQN(X,y) computes the closed-form solution to linear 
%   regression using the normal equations.

theta = zeros(size(X, 2), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
%               to linear regression and put the result in theta.
%

% ---------------------- Sample Solution ----------------------

 theta = pinv(X'*X)*X'*y;

% -------------------------------------------------------------


% ============================================================

end

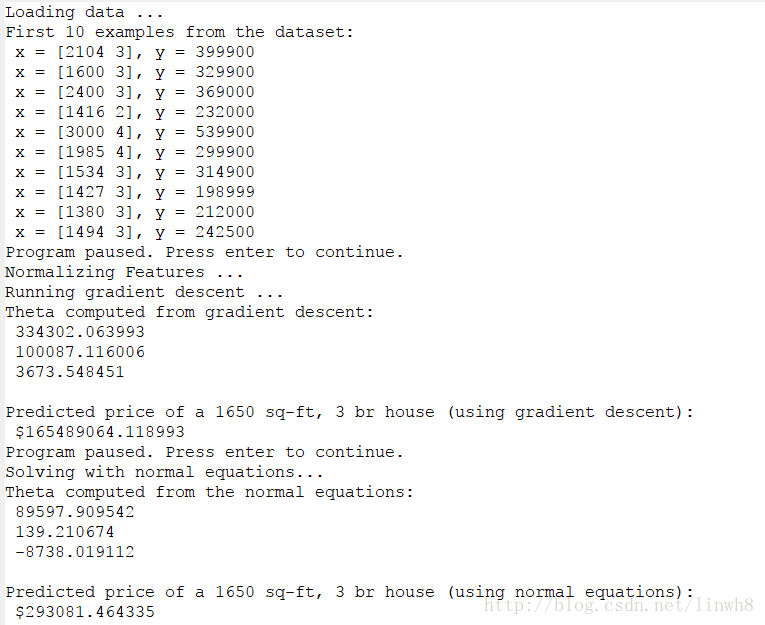
终端输出：

从输出中看到，梯度下降法与正规方程法得到的结果是不一样的，而且相差很大。很明显，梯度下降法得到的是不太可靠的，导致这样的原因是：梯度下降得到的不一定是全局最优解，很有可能是局部最优解。所以我猜测，此处的梯度下降法得到的是局部最优解，这也就是该方法的局限性所在。

4. Conclusion

这个小项目的主要难点在于：

• 将一般式子以向量化的形式表示
• Debug

---

以上内容皆为本人观点，欢迎大家提出批评和指导，我们一起探讨！

---