蓝牙定位--多点质心定位
废话不多说,直接上干货,后附已验证通过的质心算法
总体逻辑
step1
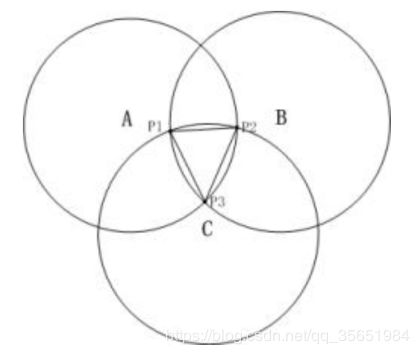
在理想环境下,已知三个信标的坐标和到坐标的距离,使用三点定位能获得三个圆的交点,从而得到位置。
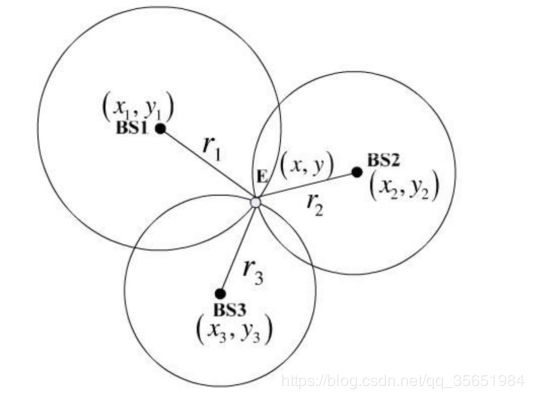
而现实情况下却情况难料。这时候使用质心法来解决复杂的位置定位
strp2
所谓质心,就是横坐标、纵坐标分别为N个点的横坐标平均值、纵坐标平均值的点。即:假定N个点的坐标分别(x1,y1),(x2,y2),……,则质心的坐标为((x1+x2+…)/N, (y1+y2+…)/N)。
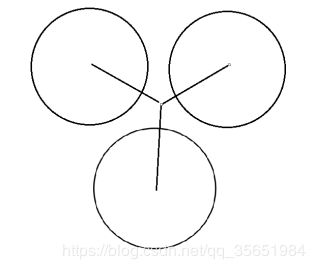
如图,p1,p2,p3交点做平均,得到的就是三个圆中心位置的质心了,每两个圆有两个交点,如何确定那些交点是p1,2,3而不是外面的三个交点呢?
step3
最小二乘法:最小二乘法思想就是求解未知参数,使得理论值与观测值之差的平方和达到最小。
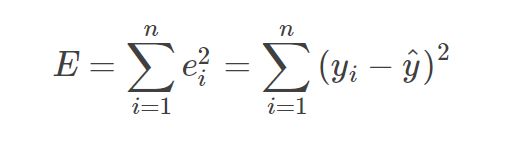
用在这里当然不是为了拟合曲线,我们可以参考最小的思想,圆1与圆2,圆3交点之间距离的平方最小的值的三个点作为p1,p2,p3。
step4
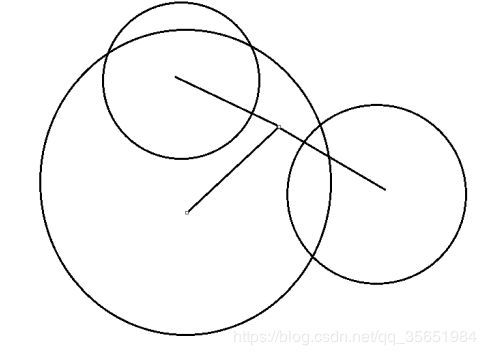
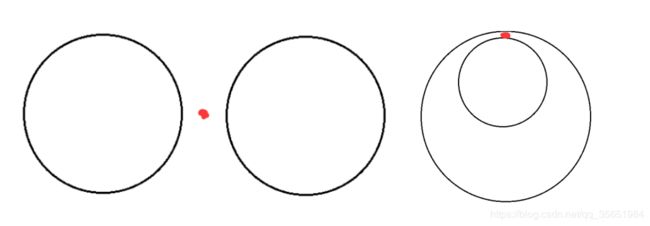
既然p1,p2,p3能求到,那么现在的问题在于如何求圆的交点,对于相交的圆是很好计算的,但相离或者包含的圆如何计算交点呢?如图,当两个圆相离或者包含时候,最佳的定位位置就是红色点的位置,所以,对于相离圆可以同时扩大两圆半径,使其相交。对于相含的圆,大圆减小半径,小圆扩大半径,使其相交。
step5
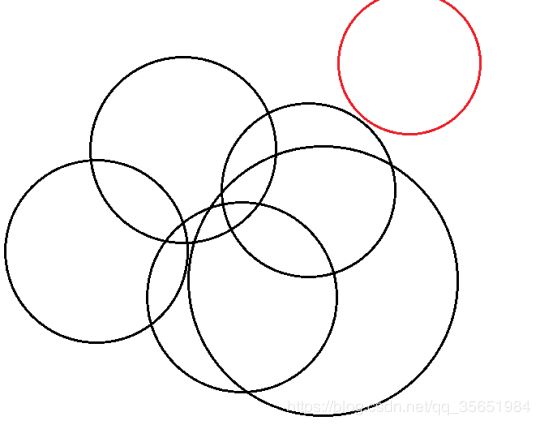
最后,三个圆两两计算获得1到2个交点,通过多个交点得到p1,p2,p3,通过这三个点计算质心。
可以在多个圆中找三个距离最近的圆计算(rssi越小确信值越高)。也可以N个圆循环选出三个圆进行计算。
将上面步骤逆向,编写代码即可
代码逻辑
step1
在装有所有圆坐标和半径的容器中循环,选出3个圆进行计算,统计所有的质点,均值后作为该点的位置坐标(list没有随机访问,只能通过迭代器,甚是麻烦)
typedef struct bea
{
string Bea_ID;
double Bea_Dis;
pair<double, double> X_Y;
}BEA_DIS;
//。。。。
for (list<BEA_DIS>::iterator it = dev_dis.Dev_Bea_Dis->begin(); it != dev_dis.Dev_Bea_Dis->end();)
{ //it 每轮自加3 为3的倍数
list<BEA_DIS>::iterator it_buf = it;//it备份
if (++it == dev_dis.Dev_Bea_Dis->end())
{
buf_data.Dev_X_Y = make_pair(buf_x_y.first / num, buf_x_y.second / num);
return buf_data;
}
auto bt = it;
if (++it == dev_dis.Dev_Bea_Dis->end())
{
buf_data.Dev_X_Y = make_pair(buf_x_y.first / num, buf_x_y.second / num);
return buf_data;
}
for (auto tt = it; tt != dev_dis.Dev_Bea_Dis->end(); ++tt)//第三个数据
{
for (; bt != tt; ++bt)//第二个数据
{
printf("$$输入三个坐标:%f,%f=%f,%f=%f,%f\n", it_buf->X_Y.first, it_buf->X_Y.second, bt->X_Y.first, bt->X_Y.second, tt->X_Y.first, tt->X_Y.second);
pair<double, double> buf= threepoint(make_pair(it_buf->Bea_Dis, it_buf->X_Y), make_pair(bt->Bea_Dis, bt->X_Y), make_pair(tt->Bea_Dis, tt->X_Y));
printf("$$输出坐标:%f::%f\n", buf.first,buf.second);
if (buf.first != 0 && buf.second != 0)
{
buf_x_y += buf;
num++;
}
}
}
it = ++it_buf;
}
step2
threepoint()函数对传入的三个圆,返回三个圆的质心
Jd()函数传入两个圆,返回两个圆的交点(1个或者两个)。取得三组交点后,计算p1,p2,p3通过这三点得到质点。参数 pair
pair<double, double> threepoint(pair<double, pair<double, double>>dev1, pair<double, pair<double, double>>dev2, pair<double, pair<double, double>>dev3)
{
pair<double, double> p1 ;// 有效交叉点1
pair<double, double> p2 ;// 有效交叉点2
pair<double, double> p3 ;// 有效交叉点3
pair<double, double> zx ;//计算三点质心
list<pair<double, double>> jds1 = jd(dev1.second.first,dev1.second.second,dev1.first, dev2.second.first, dev2.second.second, dev2.first);// r1,r2交点
list<pair<double, double>> jds2 = jd(dev1.second.first, dev1.second.second, dev1.first, dev3.second.first, dev3.second.second, dev3.first);// r1,r3交点
list<pair<double, double>> jds3 = jd(dev2.second.first, dev2.second.second, dev2.first, dev3.second.first, dev3.second.second, dev3.first);// r2,r3交点
double t = 1000000;
for (pair<double, double> jd1 : jds1)
{
for (pair<double, double> jd2 : jds2)
{
for (pair<double, double> jd3 : jds3)
{
double jd1_2_dis = sqrt(pow(jd1.first - jd2.first, 2) + pow(jd1.second - jd2.second, 2));
double jd1_3_dis= sqrt(pow(jd1.first - jd3.first, 2) + pow(jd1.second - jd3.second, 2));
double jd2_3_dis= sqrt(pow(jd2.first - jd3.first, 2) + pow(jd2.second - jd3.second, 2));
if (jd1_2_dis + jd1_3_dis + jd2_3_dis < t)
{
p1 = jd1;
p2 = jd2;
p3 = jd3;
t = jd1_2_dis + jd1_3_dis + jd2_3_dis;
}
}
}
}
zx.first = (p1.first + p2.first + p3.first) / 3;//质心
zx.second = (p1.second + p2.second + p3.second) / 3;
return zx;
}
step3
Jd两圆求交点算法。想离和包含的圆修改半径进行递归。+0.2是为了获得两个交点,更利于找到更精确的位置.。后面有时间会写一篇求两圆交点的推导。
static list<pair<double, double>> jd(double x1, double y1, double r1, double x2, double y2, double r2)
{
list<pair<double, double>>points;//交点坐标
pair<double, double> coor;
double d = sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));// 两圆心距离
if (d > r1 + r2 )
{ //相离
double buf =( d - r1 - r2 )/ 2.0+0.2;
r2 += buf;
r1 += buf;
return jd(x1,y1,r1,x2,y2,r2);
}
else if (d < abs(r1 - r2))
{
//两圆相含
return points;
double buf = (abs(r1 - r2)-d) / 2.0 + 0.2;
if (r1 > r2)//r1包含r2
{
r1 -= buf;
r2 += buf;
}
else//r2包含r1
{
r2 -= buf;
r1 += buf;
}
return jd(x1, y1, r1, x2, y2, r2);
}
else if (x1 == x2 && y1 == y2)
{
return points;// 同心圆
}
else if (y1 == y2 && x1 != x2&&d < (r1 + r2))// 两圆向交
{
double a = ((r1 * r1 - r2 * r2) - (x1 * x1 - x2 * x2)) / (2 * x2 - 2 * x1);
if (d == abs(r1 - r2) || d == r1 + r2) //圆心距==半径差或者==半径和
{
// 只有一个交点时
coor.first= a;
coor.second = y1;
points.push_back(coor);
}
else
{
// 两个交点
double t = r1 * r1 - (a - x1) * (a - x1);
coor.first = a;
coor.second= y1 + sqrt(t);
points.push_back(coor);
coor.first = a;
coor.second = y1 - sqrt(t);
points.push_back(coor);
}
}
else if (y1 != y2&&d < (r1 + r2))// 两圆向交
{
double k, disp;
k = (2 * x1 - 2 * x2) / (2 * y2 - 2 * y1);
disp = ((r1 * r1 - r2 * r2) - (x1 * x1 - x2 * x2) - (y1 * y1 - y2 * y2)) / (2 * y2 - 2 * y1);// 直线偏移量
double a, b, c;
a = (k * k + 1);
b = (2 * (disp - y1) * k - 2 * x1);
c = (disp - y1) * (disp - y1) - r1 * r1 + x1 * x1;
double disc;
disc = b * b - 4 * a * c;// 一元二次方程判别式
if (d == abs(r1 - r2) || d == r1 + r2)//圆心距==半径差或者==半径和
{
//一个交点
coor.first = (-b) / (2 * a);;
coor.second= k * coor.first + disp;
points.push_back(coor);
}
else
{
//2个交点
coor.first = ((-b) + sqrt(disc)) / (2 * a);
coor.second= k * coor.first + disp;
points.push_back(coor);
coor.first = ((-b) - sqrt(disc)) / (2 * a);
coor.second = k * coor.first + disp;
points.push_back(coor);
}
}
return points;
}