DS18B20 ROM码的搜索算法
当单线总线上挂有多个DS18B20时,系统对总线上器件的数量和每个器件ROM码的识别是通过DS18820的搜索ROM命令与算法配合来实现的。
1.ROM搜索原理
根据单线总线协议,当主机发出搜索ROM命令后,从机应答时从64位ROM码的最低位开始,先发送原码,然后发送该位的补码,之后主机写入1位数据,ROM码最低位与此数据相同的DS18B20继续应答,反之则不再应答,如此循环“读2位、写1位”的过程,直至读到一个完整ROM码为止,然后复位总线,进行下一次搜索。下面对读、写进行具体分析。
(1)读2位
由于主机发出搜索命令后,所有从机都会将自己ROM码的第一位(最低位)的原码和补码放到总线上,那么就有下面四种可能的情况:
若所有器件第一位都为0:那么所有器件放到总线上的原码都为0,补码都为1,读2位得到为“01”;若所有器件第一位都为1:同上可知,读到的值为“10”;若器件中有些为1,而有些为0:那么,放原码和补码时,都会有器件放0到总线上,根据“线与”逻辑可知读到的结果为“00”;总线上无器件:此情况下,没有器件拉低总线,读到为“11”。
(2)写1位
主机写1位的目的是为了排除和定位,具体要写入什么数据需要根据读2位的结果而定:若读到为“11”,表明无器件则结束搜索过程,无需再写入;若读到为“01”或“10”,表明所有器件此位相同,则应对应写入“0”或“1”,继续读下一位;若读到为“00”,表明总线上的器件在该位上数据发生冲突,此时,写入1位数据具有“排除”的作用,如果器件ROM编码在该位上的数据与写入的数据相同,则继续保持与总线的联系,如果不同则此器件在本次搜索中从总线上“排除”,不再响应主机发布的命令,直到主机进行下一次复位。
2.ROM搜索策略
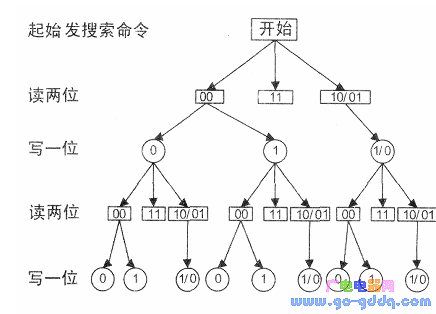
根据上述ROM搜索原理的描述,可得到如下图所示的树形搜索策略图,其中圆形节点内所示即为对应位的ROM码。
由图可知,只有遇到读两位为“00”才会出现分叉,这也是搜索的关键所在。每一次搜索由根(即开始节点)沿树的一条路径进行,直到叶子(最后一位ROM码),读回一个ROM码,为了确保每次搜索所选路径不同,必须对所经过的分又进行记录。其具体流程规则为:
(1)复位总线,发送ROM搜索命令;(2)按读两位、写一位的方式进行,寻找“00”读码。在读到“00”之前若为“10”或“01”,直接记录对应位ROM码,并写入该码;若为“11”退出搜索。
(3)第一次搜索中读到“00”时,先全部写“0”,选择ROM码为“0”的路径,将最高“00”读码(即图中最接近叶子)位置记录并保存下来为“最高00位”。
(4)之后每次搜索中,遇到“00”读码后,比较此位与“最高00位”的位置,若在“最高00位”之前,则一律写上一次搜索在此位置写入的值;若位置相同,则写“1”;若在之后则写“0”。
在每一次搜索完成后,要将“最高00位”更新为本次搜索中写“0”的最高“00”读码位置,这也是最为重要的一步。
(5)当“最高00位”更新为0,即已到树的根部,则表明已搜索完全部ROM码,过程结束。
3.ROM搜索实例
假设某一总线上挂有5个DS18820,且其ROM码分别为:xxx000、xxx001、xxx010、xxxl00和xxxl01。仅以前三位码字为例,则有如下图所示搜索树,其中共有4个分叉(即“00”读码冲突)。
根据前述算法可知其过程为:
(1)第一次搜索中,遇到“叉1”、“叉2”和“叉3”时均直接写“0”,从而得到ROM码“000”,并且“最高00位”记为3,即“又3”位置;
(2)第二次搜索时,“叉1”和“叉2”位置在“最高00位”之前,仍然写上次写的值“0”,而“又3”处,位置相同,写入“1”,同时要将“最高00位”更新为2,即“叉2”位置;本次得到ROM码为“001”;
(3)第三次搜索,到“叉2”处写“1”,并将“最高00位”更新为1,写的到ROM码“010":
(4)第四次搜索,在“叉1”处,应写“1”,但应注意的是,此时并不更新“最高00位”,要到本次搜索结束才进行更新。继续搜索,到“叉4”处,在“最高00位”之后,写“0”。本次搜索得到ROM码“100”,同时“最高00位”需更新为3,即“叉4”位置。
(5)第五次搜索,“叉1”在“最高00位”之前,仍然写上次写的值“1”,“叉4”也应写“1”,搜索结束得到ROM码“101”,而且本次搜索中没有写“0”的分叉(“00”位),因此“最高00位”更新为0,搜索结束,5个器件的ROM码已全部得到。