MATLAB基础速成
变量
MATLAB程序的基本数据单元是数组。标量在MATLAB里面也被当做数组处理,被看作只有一行一列的数组。数组可以定义为向量或矩阵,向量一般描述一维数组,矩阵一般描述二维或多维数组。数组的定义要用[]来括起来,数组中同一行元素间以空格或逗号','隔开,行与行间由分号';'隔开。
定义及赋值方式:
| 实数 |
>> x = 5 |
| 复数 |
>> x = 5 + 10i 或者>> 5 + 10j |
| 行向量 |
>> x = [1 2 3] 或者>> x = [1, 2, 3] |
| 列向量 |
>> x = [1; 2; 3] |
| 3 * 3 矩阵 |
>> x = [1 2 3; 4 5 6; 7 8 9] |
固定变量
| pi |
π |
| i, j |
|
| inf |
∞ |
| NaN |
非数 |
| ans |
默认变量 |
向量生成
1.直接生成向量
>> x = [0.00 1.00 2.00]
x =
0.00 1.00 2.00
>> x = [0.00 1.00 2.00]' %转置
x =
0.00
1.00
2.00
2.利用冒号生成向量
用两个冒号安顺序
隔开‘第一个值’,‘步增’ 和‘最后一个值’ 就可生成指定的向量. 如果步增为1, 则可以省略掉步增
和一个冒号, 比如
>> x = 1:0.5:3
x =
[1.0 1.5 2.0 2.5 3.0]
>> y = 1:3
x =
[1 2 3]
3.利用线性等分生成向量
linspace(star,end,gap) 生成一个线性等分向量
格式y=linspace(x1,x2,n)
表示生成n维向量,其中x1为第一个数,x2为最后一个数,当n默认时,系统默认生成100维向量。
例:
>>y=linspace(0,2,5)
y =
0 0.5000 1.0000 1.5000 2.0000
矩阵的生成
1.直接输入矩阵
>> a=[1,2,3;4,5,6;exp(1),7/6,abs(-2.8)]
a =
1.0000 2.0000 3.0000
4.0000 5.0000 6.0000
2.7183 1.1667 2.8000
2.利用函数生成矩阵
zeros生成全0阵
>> x=zeros(2,3)
x =
0 0 0
0 0 0
ones生成全1阵
>> y=ones(2)
y =
1 1
1 1
eye(m,n)生成单位阵
>> x=eye(2)
x =
1 0
0 1
获取向量/矩阵中的元素
指定元素所在的行和列,即可获得指定的一个或多个元素。
例:有矩阵A = [1 2 3; 4 5 6; 7 8 9]
>> x = A(1,3)
x =
3
>> y = A(2,:)
x =
[4 5 6]
>> z = A(1:2,1:2)
z =
[1 2; 4 5]
矩阵和数组运算
1.算数运算
1)基本运算
| + |
加法运算 |
| - |
减法运算 |
| * |
乘法运算 |
| / |
右除运算 |
| \ |
左除运算 |
| ^ |
指数运算 |
| ' |
转置运算 |
运算法则同线性代数
附:
x = A\B 是Ax =B 的解,而x=B/A是xA =B 的解。
2)点运算 针对同阶对应分量的运算
| .* |
乘法运算 |
| ./ |
右除运算 |
| .\ |
左除运算 |
| .^ |
指数运算 |
例:
>> A = [1 2; 3 4]
A =
1 2
3 4
>> B = A*A
B =
7 10
15 22
>> C = A.*A
C =
1 4
9 16
2.关系运算
判断两同阶数组(或者一个是矩阵,另一个是标量)对应分量间的的关系。
| < |
小于 |
| <= |
小于等于 |
| > |
大于 |
| >= |
大于等于 |
| == |
等于 |
| ~= |
不等于 |
若连个矩阵进行关系运算,则将两个矩阵对应元素逐一进行关系运算。输出结果只包含0和1。
例:
>> A = [1 3 4 2 5]
>> B = [2 1 3 5 4]
>> C = A>B % C = [1> 2, 3 >1, 4 >3, 2 >5, 5 >4]
C =
0 1 1 0 1
>> D = A<=3 % D = [1<=3, 3<=3, 4<=3, 2<=3, 5<=3]
D =
1 1 0 1 0
3.逻辑运算
| & |
与 |
| | |
或 |
| ~ |
非 |
例:
>> A = [1 3 4 2 5];
>> B = [2 1 3 5 4];
>> C = (A>B) & (A<=3)
C =
0 1 0 0 0
常用数学函数
| sin |
正弦 |
Asin |
反正弦 |
| cos |
余弦 |
acos |
反余弦 |
| tan |
正切 |
atan |
反正切 |
| cot |
余切 |
acot |
反余切 |
| Exp |
指数函数 |
Sqrt |
平方根 |
| Log |
自然对数 |
log10 |
以10 为底的对数 |
| abs |
绝对数 |
sign |
符号函数 |
以上函数是针对矩阵对应元素逐一进行函数的运算。
例:
>> theta = 0:pi/3:pi
theta =
0 1.0472 2.0944 3.1416
>> sin(theta)
ans =
0 0.8660 0.8660 0.0000
数组操作函数
| rot90(A) |
将A逆时针方向旋转90° |
| rot90(A,K) |
将A逆时针方向旋转(90*K)° |
| fliplr(A) |
将矩阵A左右翻转 |
| flipud(A) |
将矩阵A上下翻转 |
| flipdim(A,dim) |
将矩阵A的dim维翻转,dim=1表示行,dim=2表示列 |
| max |
输出最大数 |
| min |
输出最小数 |
| sum |
求和 |
例:
flipud, fliplr, rot90
>> A = [1 2 3; 4 5 6; 7 8 9];
>> B = flipud(A)
A =
7 8 9
4 5 6
1 2 3
>> C = rot90(A)
C =
3 6 9
2 5 8
1 4 7
sum
多维时默认求各列之和,若后加2则求各行之和
>> A = [1 2 3];
>> sum(A)
ans =
6
>> B = [1 2 3; 4 5 6; 7 8 9];
>> sum(B)
ans =
12 15 18
>> sum(B,2)
ans =
6
15
25
>> sum(B(:)) %求所有项总和
ans =
45
max,min
>> A = [1 2 3];
>> max(A)
ans =
3
>> max(A,2) 将A中所有元素与2比较
ans =
2 2 3
>> B = [1 3 9; 4 8 6]; B为2维按照每列取最大值
>> max(B)
ans =
4 8 9
>> max(B, [], 2)
ans =
9
8
基本语句
for .. end
if .. else .. end
while .. end
switch .. case .. end
例:求1-10 以内的奇数和
% sum of the odd numbers between 1 and 10
x = 0;
for i = 1:10
if mod(i,2)
x= x + i;
end
end
简单作图
plot(x,y,'s')
其中x表示横坐标向量,y表示纵坐标向量,s为选项字符串,用于控制线型与颜色。常用表示见绘图参数表。
title(图形名称)
xlabel(x 轴说明); ylabel(y 轴说明)
text(x,y, 图形说明)
legend(图例1, 图例2, ...)
grid on / grid off / grid minor
axis([xmin xmax ymin ymax]), xlim([xmin, xmax])
绘图参数表
| b |
蓝 |
. |
点 |
^ |
向上三角形 |
- |
实线 |
| g |
绿 |
o |
圆 |
< |
向左三角形 |
: |
点线 |
| r |
红 |
x |
叉号 |
|
向右三角形 |
-. |
点划线 |
| c |
青 |
+ |
加号 |
p |
五角星 |
-- |
虚线 |
| m |
紫 |
|
星号 |
h |
六角星 |
|
|
| y |
黄 |
s |
正方形 |
|
|
|
|
| k |
黑 |
d |
菱形 |
|
|
|
|
| w |
白 |
v |
向下三角形 |
|
|
|
|
例1:
x=-2*pi:0.1:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'-b');
hold on %图像保持
plot(x,y2,'-r');
xlabel('X')
ylabel('Y')
text(0,0,'(0,0)')
legend('sinx','conx')
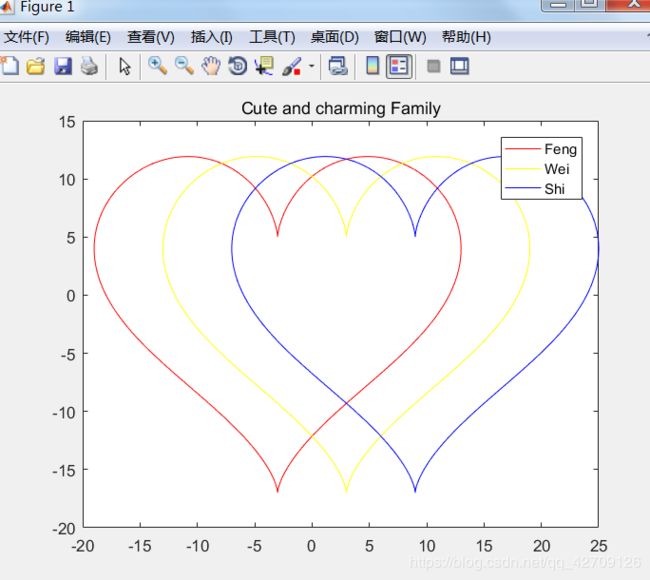
例2:
%建模一家
t=0:pi/180:4*pi;
x=16*sin(t).^3;
y=13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t);
plot(x-3,y,'-r',x+3,y,'-y',x+9,y,'-b');
axis([-20,25,-20,15]);
title('Cute and charming Family')
legend('Feng','Wei','Shi')
注:本文是我学习MATLAB时整理的笔记,方便日后查看复习。分享给大家,文中可能有一些错误,或简陋难以理解的地方,大家可以指正,共同进步。(部分内容参照网上资料,侵删)