【Paper Note】DCN——Deep & Cross Network for Ad Click Prediction论文翻译（中英文对照）

Abstract

Feature engineering has been the key to the success of many prediction models. However, the process is nontrivial and o en requires manual feature engineering or exhaustive searching. DNNs are able to automatically learn feature interactions; however, they generate all the interactions implicitly, and are not necessarily efficient in learning all types of cross features. In this paper, we propose the Deep & Cross Network (DCN) which keeps the benefits of a DNN model, and beyond that, it introduces a novel cross network that is more efficient in learning certain bounded-degree feature interactions. In particular, DCN explicitly applies feature crossing at each layer, requires no manual feature engineering, and adds negligible extra complexity to the DNN model. Our experimental results have demonstrated its superiority over the state-of-art algorithms on the CTR prediction dataset and dense classification dataset, in terms of both model accuracy and memory usage.

摘要

特征工程一直是许多预测模型成功的关键。然而这个过程是重要的，而且经常需要手动进行特征工程或遍历搜索。DNN可以自动地学习特征地交互作用，然而，它们隐式地的生成所有的特征交互，这对于学习所有类型的交叉特征不一定有效。在本文中，我们提出了一种能够保持深度神经网络良好收益的深度交叉网络（DCN），除此之外，它还引入了一个新的交叉网络，更有效地学习在一定限度下的特征相互作用，更有甚，DCN在每一层确切地应用交叉特征而不需要人工特征工程，这相比于DNN模型增加地额外地复杂度可以忽略不计。我们的实验证明它在CTR预测数据机和稠密分类数据机上具有优越性能。

1 INTRODUCTION

Click-through rate (CTR) prediction is a large-scale problem that is essential to multi-billion dollar online advertising industry. In the advertising industry, advertisers pay publishers to display their ads on publishers’ sites. One popular payment model is the cost-per-click (CPC) model, where advertisers are charged only when a click occurs. As a consequence, a publisher’s revenue relies heavily on the ability to predict CTR accurately.
Identifying frequently predictive features and at the same time exploring unseen or rare cross features is the key to making good predictions. However, data for Web-scale recommender systems is mostly discrete and categorical, leading to a large and sparse feature space that is challenging for feature exploration. This has limited most large-scale systems to linear models such as logistic regression.
Linear models [3] are simple, interpretable and easy to scale; however, they are limited in their expressive power. Cross features, on the other hand, have been shown to be significant in improving the models’ expressiveness. Unfortunately, it o en requires manual feature engineering or exhaustive search to identify such features; moreover, generalizing to unseen feature interactions is difficult.
In this paper, we aim to avoid task-specific feature engineering by introducing a novel neural network structure – a cross network – that explicitly applies feature crossing in an automatic fashion.
The cross network consists of multiple layers, where the highest- degree of interactions are provably determined by layer depth. Each layer produces higher-order interactions based on existing ones, and keeps the interactions from previous layers. We train the cross network jointly with a deep neural network (DNN) [10, 14]. DNN has the promise to capture very complex interactions across features; however, compared to our cross network it requires nearly an order of magnitude more parameters, is unable to form cross features explicitly, and may fail to efficiently learn some types of feature interactions. Jointly training the cross and DNN components together, however, efficiently captures predictive feature interactions, and delivers state-of-the-art performance on the Criteo CTR dataset.

1 介绍

点击率（CTR）预测是一个大规模问题，对于数十亿美元的广告业来说至关重要，在广告业，广告商付钱给出版商，以便在它们的网站上发布广告，一种流行的付费模式是单次点击付费（CPC）模型，广告商只在用户点击时收取费用，因此，出版商的收入在很大程度上依赖于准确预测CTR的能力。
识别频繁的预测特征，同时探索隐式的或罕见的交叉特征是做好预测的关键，然而，Web规模推荐系统的数据大多是离散的和分类的，导致大量和稀疏的特征空间，这是具有挑战性的特征探索，这也限制了大多数大型系统的线性模型，如logistic回归。
线性模型简单、可解释、容易扩展，但限制了模型的表达能力，另一方面，交叉特征在提高模型表达能力方面具有重要意义，不幸的是，它常常需要人工特征工程或遍历搜索来识别这些特征；此外，泛化到隐式的特征交互是困难的。
在本文中，我们的目标是通过引入一种新的神经网络结构（跨网络）来避免特定于任务的特征工程，它以自动方式显式地应用特征交叉。交叉网络由多个层组成，其中层的深度可以证明交互作用的最高程度，每个层基于现有的层产生高阶交互，并保持与先前层的交互，我们跨网联合深层神经网络（DNN）进行训练[ 10, 14 ]，DNN已经捕捉到非常复杂的相互作用的有限元分析，然而，相比我们的跨网络需要近一个数量级以上的参数，无法形成明确的交叉特征，可能无法有效地学习特征相互作用的类别。联合训练的交叉网络和DNN的组分能够有效地捕获预测特征的关系，并在Criteo CTR数据集上获得优越性能。

1.1 Related Work

Due to the dramatic increase in size and dimensionality of datasets, a number of methods have been proposed to avoid extensive task-specific feature engineering, mostly based on embedding techniques and neural networks.
Factorization machines (FMs) [11, 12] project sparse features onto low-dimensional dense vectors and learn feature interactions from vector inner products. Field-aware factorization machines (FFMs) [7, 8] further allow each feature to learn several vectors where each vector is associated with a field. Regrettably, the shallow structures of FMs and FFMs limit their representative power. There have been work extending FMs to higher orders [1, 18], but one downside lies in their large number of parameters which yields undesirable computational cost. Deep neural networks (DNN) are able to learn non-trivial high-degree feature interactions due to embedding vectors and nonlinear activation functions. The recent success of the Residual Network [5] has enabled training of very deep networks. Deep Crossing [15] extends residual networks and achieves automatic feature learning by stacking all types of inputs.
The remarkable success of deep learning has elicited theoretical analyses on its representative power. There has been research [16, 17] showing that DNNs are able to approximate an arbitrary function under certain smoothness assumptions to an arbitrary accuracy, given sufficiently many hidden units or hidden layers. Moreover, in practice, it has been found that DNNs work well with a feasible number of parameters. One key reason is that most functions of practical interest are not arbitrary.
Yet one remaining question is whether DNNs are indeed the most efficient ones in representing such functions of practical interest. In the Kaggle1 competition, the manually craed features in many winning solutions are low-degree, in an explicit format and effective. e features learned by DNNs, on the other hand, are implicit and highly nonlinear. is has shed light on designing a model that is able to learn bounded-degree feature interactions more efficiently and explicitly than a universal DNN.
The wide-and-deep [4] is a model in this spirit. It takes cross features as inputs to a linear model, and jointly trains the linear model with a DNN model. However, the success of wide-and-deep hinges on a proper choice of cross features, an exponential problem for which there is yet no clear efficient method.

1.1 相关工作

由于数据集规模和维数的急剧增加，已经提出了许多方法，用来避免大规模特定任务的特征工程，主要是基于嵌入技术和神经网络。
因子机（FMs）[ 11, 12 ]将稀疏特征投射到低维稠密向量上，学习向量内积的特征相互作用，场意识的分解机（FFMs）[ 7, 8 ]进一步允许每个特征向量，每个向量学习的几个与字段关联，遗憾地是，浅层低结构的FMS和FMMs限制他们的表达能力，已经有工作扩展FMS到更高的等级[ 1, 18 ]，但缺点在于他们大量的参数会产生更大的计算成本。深度神经网络（DNN）能够学习不平凡的高程度特征相互作用由于嵌入载体和非线性激活函数，最近非常成功的残差网络[5]使非常深网络的训练成为可能，DCN[ 15 ]扩展了残差网络，通过叠加所有类型的输入实现自动的特征学习。
深度学习的显著成功，引发了对其表达能力上的理论分析，已经有研究[ 16, 17 ]表明DNN能够逼近任意函数的某些平滑假设下的任意的精度，给出了足够多的隐藏单元或隐藏层，此外，在实践中，已发现DNNs工作以及可行的参数个数。其中一个关键原因在于实际兴趣的大部分功能并不是任意的。
然而，还有一个问题是，DNN是否真的表达出实际利益最有效的功能。在kaggle竞赛中，人工生成的特征在许多获奖的解决方案中处于低程度，具有显式格式和有效性，了解到DNN的特点是内隐的、高度非线性的，这揭示了一个模型能够比通用的DNN设计更能够有效地学习的有界度特征相互作用。
W&D网络[ 4 ]是这种精神的典范。它以交叉特征作为一个线性模型的输入，与一个DNN模型一起训练线性模型，然而，W&D网络的成功取决于正确的交叉特征的选择，这是一个至今还没有明确有效的方法解决的指数问题。

1.2 Main Contributions

In this paper, we propose the Deep & Cross Network (DCN) model that enables Web-scale automatic feature learning with both sparse and dense inputs. DCN efficiently captures effective feature interactions of bounded degrees, learns highly nonlinear interactions, requires no manual feature engineering or exhaustive searching, and has low computational cost.
The main contributions of the paper include:
• We propose a novel cross network that explicitly applies feature crossing at each layer, efficiently learns predictive cross features of bounded degrees, and requires no manual feature engineering or exhaustive searching.
• The cross network is simple yet effective. By design, the highest polynomial degree increases at each layer and is determined by layer depth. The network consists of all the cross terms of degree up to the highest, with their coefficients all different.
• The cross network is memory efficient, and easy to implement.
• Our experimental results have demonstrated that with a cross network, DCN has lower logloss than a DNN with nearly an order of magnitude fewer number of parameters.
The paper is organized as follows: Section 2 describes the architecture of the Deep & Cross Network. Section 3 analyzes the cross network in detail. Section 4 shows the experimental results.

1.2 主要贡献

在本文中，我们提出了深度交叉网络（DCN）模型，使网络规模的自动进行稀疏和密集输入的特征学习，DCN有效地捕获有限度的有效特征的相互作用，学会高度非线性的相互作用，不需要人工特征工程或遍历搜索，并具有较低的计算成本。
论文的主要贡献包括：

• 我们提出了一种新的交叉网络，在每个层上明确地应用特征交叉，有效地学习有界度的预测交叉特征，并且不需要手工特征工程或穷举搜索。
• 跨网络简单而有效。通过设计，各层的多项式级数最高，并由层深度决定。网络由所有的交叉项组成，它们的系数各不相同。
• 跨网络内存高效，易于实现。
• 我们的实验结果表明，交叉网络（DCN）在LogLoss上与DNN相比少了近一个量级的参数量。

本文的结构如下：第2节描述了深层和交叉网络的体系结构。第3部分详细分析了交叉网络。第4节给出了实验结果。

2 DEEP & CROSS NETWORK (DCN)

In this section we describe the architecture of Deep & Cross Network (DCN) models. A DCN model starts with an embedding and stacking layer, followed by a cross network and a deep network in parallel. These in turn are followed by a final combination layer which combines the outputs from the two networks. The complete DCN model is depicted in Figure 1.

2 深度交叉网络（DCN）

在本节中我们介绍深度交叉网络的体系结构（DCN）模型。一个DCN模型从嵌入和堆积层开始，接着是一个交叉网络和一个与之平行的深度网络，之后是最后的组合层，它结合了两个网络的输出。完整的网络模型如图1所示。

2.1 Embedding and Stacking Layer

We consider input data with sparse and dense features. In Web-scale recommender systems such as CTR prediction, the inputs are mostly categorical features, e.g. “country=usa”. Such features are often encoded as one-hot vectors e.g. “[0,1,0]”; however, this often leads to excessively high-dimensional feature spaces for large vocabularies.

To reduce the dimensionality, we employ an embedding proce- dure to transform these binary features into dense vectors of real values (commonly called embedding vectors):$$x_{embed,i}=W_{embed,i}{x}_i(1)$$ where $x_{embed,i}$ is the embedding vector, $x_i$ is the binary input in the i-th category, and $W_{embed,i}$ ∈ $R^{n_e\times n_v}$ is the corresponding embedding matrix that will be optimized together with other parameters in the network, and $n_e$ , $n_v$ are the embedding size and vocabulary size, respectively.
In the end, we stack the embedding vectors, along with the normalized dense features $x_{dense}$ , into one vector: $$x_0=[x_{embed,1}^T,\cdots ,x_{embed,k}^T,x_{dense}^T](2)$$ and feed $x_0$ to the network.

2.1 嵌入和堆叠层

我们考虑具有稀疏和密集特征的输入数据。在网络规模推荐系统中，如CTR预测，输入主要是分类特征，如“country=usa”。这些特征通常是编码为独热向量如“[ 0,1,0 ]”；然而，这往往导致过度的高维特征空间大的词汇。
为了减少维数，我们采用嵌入过程将这些二进制特征转换成实数值的稠密向量（通常称为嵌入向量）：$$x_{embed,i}=W_{embed,i}{x}_i(1)$$ 其中，$x_{embed,i}$ 是嵌入向量， $x_i$ 是第i层的二元输入，$W_{embed,i}$ ∈ $R^{n_e\times n_v}$ 是与网络中的其他参数一起优化的相应的嵌入矩阵， $n_e$ , $n_v$ 分别是嵌入大小和词汇大小，最后，我们将嵌入向量与归一化稠密特征$x_{dense}$叠加起来形成一个向量：$$x_0=[x_{embed,1}^T,\cdots ,x_{embed,k}^T,x_{dense}^T](2)$$ $x_0$ 就是网络的输入。

2.2 Cross Network

The key idea of our novel cross network is to apply explicit feature crossing in an efficient way. The cross network is composed of cross layers, with each layer having the following formula:$$x_{l+1}=x_0{x}_l^T{w}_l+b_l+x_l=f(x_l,w_l,b_l)+x_l(3)$$ where $x_l,x_{l+1}\in R^d$ are column vectors denoting the outputs from the $l$-th and $(l+1)$-th cross layers, respectively; $w_l,b_l\in R^d$ are the weight and bias parameters of the $l$-th layer. Each cross layer adds back its input after a feature crossing $f$ , and the mapping function $f:R^d\to R^d$ fits the residual of $x_{l+1}-x_l$ . A visualization of one cross layer is shown in Figure 2.
High-degree Interaction Across Features. The special structure of the cross network causes the degree of cross features to grow with layer depth. The highest polynomial degree (in terms of input $x_0$ ) for an $l$ -layer cross network is $l+1$. In fact, the cross network comprises all the cross terms $x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_d^{{\alpha }_d}$ of degree from 1 to $l+1$. Detailed analysis is in Section 3.

Complexity Analysis. Let $L_c$ denote the number of cross layers, and $d$ denote the input dimension. en, the number of parameters involved in the cross network is$$d\times L_c\times 2$$ The time and space complexity of a cross network are linear in input dimension. Therefore, a cross network introduces negligible complexity compared to its deep counterpart, keeping the overall complexity for DCN at the same level as that of a traditional DNN. This efficiency benefits from the rank-one property of $x_0{x}_l^T$ ,which enables us to generate all cross terms without computing or storing the entire matrix.
The small number of parameters of the cross network has limited the model capacity. To capture highly nonlinear interactions, we introduce a deep network in parallel.

2.2 交叉网络

我们的交叉网络的核心思想是以有效的方式应用显式特征交叉。交叉网络由交叉层组成，每个层具有以下公式：$$x_{l+1}=x_0{x}_l^T{w}_l+b_l+x_l=f(x_l,w_l,b_l)+x_l(3)$$ 其中，$x_l,x_{l+1}\in R^d$表示 $l$ 层和 $l+1$ 层输出的列向量。每个交叉层在特征越过F之后添加其输入，而映射函数$\ f\ $为：$ R^d → R^d$ ，残差符合 $x_{l+1}-x_l$ ，一个交叉层的可视化如图2所示。

交叉特征高度交互。交叉网络的特殊结构使交叉特征的程度随着层深度的增加而增大。多项式的最高程度（就输入X0而言）为L层交叉网络L + 1。事实上，交叉网络包含了从1到L1的所有交叉项。详细分析见第3节。
复杂度分析。 $L_c$表示交叉层数，$d$表示输入维度。然后，参数的数量参与跨网络参数为：$$d\times L_c\times 2$$ 交叉网络的时间和空间复杂度在输入维度上是线性的。因此，一个跨网络引入了可以忽略不计的复杂性相比，其深刻的对应，DCN的整体复杂性保持在相同的水平，一个传统的DNN。这种效率得益于$x_0{x}_l^T$的rank-one性质，它使我们能够在不计算或存储整个矩阵的情况下生成所有交叉项。
交叉网络的少数参数限制了模型容量。为了捕捉高度非线性的相互作用，我们并行地引入了一个深度网络。

2.3 Deep Network

The deep network is a fully-connected feed-forward neural network, with each deep layer having the following formula:$$h_{l+1}=f(W_l{h}_l+b_l)(4)$$where $h_l\in R_l^n,h_{l+1}\in R_{l+1}^n$ are the $l$-th and $(l+1)$-th hidden layer, respectively; $W_l\in R_{l+1}^n\times n_l,b_l\in R_{l+1}^n$ are parameters for the $l$-th deep layer; and $f(\cdot )$ is the ReLU function.
Complexity Analysis. For simplicity, we assume all the deep layers are of equal size. Let $L_d$ denote the number of deep layers and $m$ denote the deep layer size. Then, the number of parameters in the deep network is $$d\times m+m+(m^2+m)\times (L_d-1)$$

2.4 Combination Layer

The combination layer concatenates the outputs from two networks and feed the concatenated vector into a standard logits layer.
The following is the formula for a two-class classification problem:
$$p=\sigma ([x_{L_1}^T,h_{L_2}^T]w_{logits})\text{\hspace{1em}(5)}$$
where $x_{L_1}\in R^d,h_{L_2}\in R^m$ are the outputs from the cross network and deep network, respectively, $w\in R^{(d+m)}$ is the weight
vector for the combination layer, and $\sigma (x)=1/(1+exp(-x))$.
The loss function is the log loss along with a regularization term,
$$loss=-\frac{1}{N}\sum _{i=1}^N{y}_{i}log(p_i)+(1-y_i)log(1-p_i)+\lambda \sum _l\Vert w_l{\Vert }^2\text{\hspace{1em}(6)}$$
where $p_i$’s are the probabilities computed from Equation 5, $y_i$’s are the true labels, $N$ is the total number of inputs, and $\lambda$ is the $L_2$ regularization parameter.
We jointly train both networks, as this allows each individual network to be aware of the others during the training.

2.3深度网络

深度网络就是一个全连接的前馈神经网络，每个深度层具有如下公式：$$h_{l+1}=f(W_l{h}_l+b_l)(4)$$ 其中， $h_l\in R_l^n,h_{l+1}\in R_{l+1}^n$ 是第$\ l\ $ 层和第$l+1$ 层的隐藏层，$W_l\in R_{l+1}^n\times n_l,b_l\in R_{l+1}^n$是第$\ l\ $ 层的参数， $f(\cdot )$ 是ReLU激活函数。
复杂度分析。简单起见，我们假设所有的深层都是一样大小的。 $L_d$ 表示层的深度，$m$ 表示深层尺寸。在深度网络中，参数量为：$$d\times m+m+(m^2+m)\times (L_d-1)$$

2.4融合层

融合层链接两个网络并将连接向量输入到标准的逻辑回归函数中。
下面的公式为一个二分类问题：
$$p=\sigma ([x_{L_1}^T,h_{L_2}^T]w_{logits})\text{\hspace{1em}(5)}$$
其中， $x_{L_1}\in R^d,h_{L_2}\in R^m$ 为cross网络和deep网络的输出， $w\in R^{(d+m)}$ 是融合层的权重，并且 $\sigma (x)=1/(1+exp(-x))$.

3 CROSS NETWORK ANALYSIS

In this section, we analyze the cross network of DCN for the purpose of understanding its. We offer three perspectives: polynomial approximation, generalization to FMs, and efficient projection. For simplicity, we assume $b_i=0$.
Notations. Let the $i$-th element in $w_j$ be $w_j^{(i)}$. For multi-index
$\alpha =[\alpha 1,\cdot \cdot \cdot ,\alpha d]\in N^d$ and $x=[x_1,\cdot \cdot \cdot ,x_d]\in Rd$, we define $|\alpha |=d_i={\sum }_{i=1}^d{\alpha }_i$.
Terminology. The degree of across term (monomial) $x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdot \cdot \cdot x_d^{{\alpha }_d}$ is defined by $|\alpha |$. The degree of a polynomial is defined by the highest degree of its terms.

3. 交叉网络分析

在这一节中，我们将分析DCN的交叉网络来理解它的作用。我们提出了三个看法：多项式近似，泛化FM和有效的映射。简单起见，假设$b_i=0$。
注意，令第i层元素的权重表示为$w_j^{(i)}$，对于多下标：$\alpha =[\alpha 1,\cdot \cdot \cdot ,\alpha d]\in N^d$ 和 $x=[x_1,\cdot \cdot \cdot ,x_d]\in Rd$, 定义 $|\alpha |=d_i={\sum }_{i=1}^d{\alpha }_i$。
术语。将$x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdot \cdot \cdot x_d^{{\alpha }_d}$交叉项定义为$|\alpha |$，多项式定义为它的高阶项。

3.1 Polynomial Approximation

By the Weierstrass approximation theorem [13], any function under certain smoothness assumption can be approximated by a polynomial to an arbitrary accuracy. Therefore, we analyze the cross network from the perspective of polynomial approximation. In particular, the cross network approximates the polynomial class of the same degree in a way that is efficient, expressive and generalizes better to real-world datasets.
We study in detail the approximation of a cross network to the polynomial class of the same degree. Let us denote by $P_n(x)$ the multivariate polynomial class of degree $n$:
$$P_n(x)=\{\sum _{\alpha }{w}_{\alpha }{x}_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_d^{{\alpha }_d}|0<=|\alpha |<=n,\alpha \in N^d\}\text{\hspace{1em}(7)}$$
Each polynomial in this class has $O(d^n)$ coefficients. We show that, with only $O(d)$ parameters, the cross network contains all the cross terms occurring in the polynomial of the same degree, with each term’s coefficient distinct from each other.
Theorem 3.1. Consider an l-layer cross network with the i+1-th layer defined as $xi+1=x0xTiwi+xi$ . Let the input to the network be $x_0=[x_1,x_2,\cdots ,x_d]T$, the output be $g_l(x0)=x_l^T{w}_l$, and the parameters be $w_i,b_i\in R^d$. Then, the multivariate polynomial $g_l(x_0)$ reproduces polynomials in the following class:
$$\{\sum _{\alpha }{c}_{\alpha }(w_0,\cdots ,w_l)x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_d^{{\alpha }_d}|0\le |\alpha |\le l+1,\alpha \in N^d\}$$ where $c_{\alpha }=M_a{\sum }_{i\in B_{\alpha }}{\sum }_{j\in P_{\alpha }}{\prod }_{k=1}^{|\alpha |}{w}_{i_k}^{(j_k)},M_{\alpha }$ is a constant independent of $w_i$'s, $i=[i_1,\cdots ,i_{|\alpha |}]$ and $j=[j_1,\cdots ,j_{|\alpha |}]$ are multi-indices, $B_{\alpha }=\{y\in \{0,1,\cdots ,l{\}}^{|\alpha |}|y_i<y_j\bigwedge y_{\alpha }=l\}$, and $p_{\alpha }$ is the set of all the permutations of the indices$(\underset{{\alpha }_{1}times}{1,\cdots ,1}\cdots \underset{{\alpha }_{d}times}{d,\cdots ,d})$.
The proof of Theorem 3.1 is in the Appendix. Let us give an example. Consider the coefficient $c_{\alpha }$ for $x_1{x}_2{x}_3$ with $\alpha =(1,1,1,0,\cdots ,0)$. Up to some constant, when $l=2,c_{\alpha }={\sum }_{i,j,k\in P_{\alpha }}{w}_0^{(i)}{w}_1^{(j)}{w}_2^{(k)}$; when $l=3,c_{\alpha }={\sum }_{i,j,k\in P_{\alpha }}{w}_0^{(i)}{w}_1^{(j)}{w}_3^{(k)}+w_0^{(i)}{w}_2^{(j)}{w}_3^{(k)}+w_1^{(i)}{w}_2^{(j)}{w}_3^{(k)}$.

3.1 多项式近似

根据Weierstrass近似理论，任何函数在某些平滑假设可以用一个多项式近似任意精度。因此,我们分析了交叉网络从多项式近似的角度。特别是交叉网络近似多项式类相同的学位是有效的方式,表达和概括现实世界的数据集。
我们将近似一个交叉网络来详细研究同阶多项式。令$P_n(x)$表示n阶多元多项式：
$$P_n(x)=\{\sum _{\alpha }{w}_{\alpha }{x}_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_d^{{\alpha }_d}|0\le |\alpha |\le n,\alpha \in N^d\}\text{\hspace{1em}(7)}$$
每个多项式在这类上都有 $O(d^n)$系数。我们表明,只有 $O(d^n)$的参数、交叉网络包含所有的交叉项发生在多项式相同的程度,每一项的系数彼此不同。
定理 3.1。考虑一个$l$层交叉网络，$l+1$层可以定义为 $xi+1=x0xTiwi+xi$。使网络的输入为$x_0=[x_1,x_2,\cdots ,x_d]T$, 输出为 $g_l(x0)=x_l^T{w}_l$，并且参数为$w_i,b_i\in R^d$。那么，多元多项式$g_l(x_0)$产生一下情形：
$$\{\sum _{\alpha }{c}_{\alpha }(w_0,\cdots ,w_l)x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_d^{{\alpha }_d}|0\le |\alpha |\le l+1,\alpha \in N^d\}$$其中， $c_{\alpha }=M_a{\sum }_{i\in B_{\alpha }}{\sum }_{j\in P_{\alpha }}{\prod }_{k=1}^{|\alpha |}{w}_{i_k}^{(j_k)},M_{\alpha }$ 是$w_i$的一个独立常数, $i=[i_1,\cdots ,i_{|\alpha |}]$ 和 $j=[j_1,\cdots ,j_{|\alpha |}]$ 是多指标, $B_{\alpha }=\{y\in \{0,1,\cdots ,l{\}}^{|\alpha |}|y_i<y_j\bigwedge y_{\alpha }=l\}$, 并且 $p_{\alpha }$ 是指标$(\underset{{\alpha }_{1}times}{1,\cdots ,1}\cdots \underset{{\alpha }_{d}times}{d,\cdots ,d})$的所有排列。

3.2 Generalization of FMs

The cross network shares the spirit of parameter sharing as the FM model and further extends it to a deeper structure.

In a FM model, feature $x_i$ is associated with a weight vector $v_i$ , and the weight of cross term $x_i{x}_j$ is computed by $⟨v_i,v_j⟩$. In DCN, $x_i$ is associated with scalars $\{w_k^{(i)}{\}}_{k=1}^l$ , and the weight of $x_i{x}_j$ is the multiplications of parameters from the sets $\{w_k^{(i)}{\}}_{k=0}^l$ and $\{w_k^{(j)}{\}}_{k=0}^l$ . Both models have each feature learned some parameters independent from other features, and the weight of a cross term is a certain combination of corresponding parameters.

Parameter sharing not only makes the model more efficient, but also enables the model to generalize to unseen feature interactions and be more robust to noise. For example, take datasets with sparse features. If two binary features $x_i$ and $x_j$ rarely or never co-occur in the training data, i.e., $x_i̸=0\bigwedge x_j̸=0$, then the learned weight of $x_i{x}_j$ would carry no meaningful information for prediction.

The FM is a shallow structure and is limited to representing
cross terms of degree 2. DCN, in contrast, is able to construct all the
cross terms $x_1^{{\alpha }_1}{x}_2^{\alpha 2}\cdots x_d^{{\alpha }_d}$ with degree $|\alpha |$ bounded by some constant determined by layer depth, as claimed in Theorem 3.1. Therefore, the cross network extends the idea of parameter sharing from a single layer to multiple layers and high-degree cross-terms. Note that different from the higher-order FMs, the number of parameters in a cross network only grows linearly with the input dimension.

3.2 泛化FMs

交叉网络共享参数共享的灵感和FM模型一样，进一步延伸到更深层次的结构。
在FM模型中，特征$x_i$和权重向量$v_i$相关联，交叉项 $x_i{x}_j$ 的权重由 $⟨v_i,v_j⟩$计算。在DCN模型中，$x_i$和标量$\{w_k^{(i)}{\}}_{k=1}^l$相关联，并且$x_i{x}_j$的权重从集合$\{w_k^{(i)}{\}}_{k=0}^l$ 和 $\{w_k^{(j)}{\}}_{k=0}^l$中计算而来。两种模型每个特性学到了一些参数独立于其他功能,和交叉项的重量是一个特定组合的相应参数。
参数共享不仅使模型更有效,但也使交互模型推广到看不见的特性和更健壮的噪音。例如,以具有稀疏特征的数据集，如果两个二进制特征$x_i$ 和 $x_j$ 很少或从不共现的训练数据，如$x_i̸=0\bigwedge x_j̸=0$，然后$x_i{x}_j$ 学到的权重将没有有意义的信息用以预测。
FM是一个浅结构和有限代表交叉项。相比之下，DCN可以构建所有的交叉项$x_1^{{\alpha }_1}{x}_2^{\alpha 2}\cdots x_d^{{\alpha }_d}$与 $|\alpha |$ ,通过层的深度获得界限，定理3.1。因此，交叉网络扩展参数共享的概念从一个单层到多层和高度交叉项。注意，不同的高阶FMs，参数的个数与交叉网络只会增加线性输入维数。

3.3 Efficient Projection

Each cross layer projects all the pairwise interactions between $x_0$ and $x_l$ , in an efficient manner, back to the input’s dimension.
Consider $\breve{x}\in R^d$ as the input to a cross layer. The cross layer first implicitly constructs $d_2$ pairwise interactions $x_i\breve{x_j}$, and then implicitly projects them back to dimension d in a memory-efficient way. A direct approach, however, comes with a cubic cost.

Our cross layer provides an efficient solution to reduce the cost
to linear in dimension $d$ . Consider $x_p=x_0{\breve{x}}^{T}w$. This is in fact equivalent to

where the row vector contains all $d^2$ pairwise interactions $x_i{\breve{x}}_j$’s, the projection matrix has a block diagonal structure with $w\in R^d$ being a column vector.

3.3 有效的映射

每个交叉层项目所有成对$x_0$和$x_l$ 之间的相互作用,在一个有效的方式,回到输入的维度。
考虑 $\breve{x}\in R^d$作为输入交叉层。跨层第一隐式构造$d_2$ 和$x_i\breve{x_j}$两两交互,然后隐式项目他们回到 $d$ 维节约内存。一个直接的方法,然而,附带了一个立方的成本。
我们交叉层提供了一个有效的解决方案，以在d维空间降低线性成本。考虑$x_p=x_0{\breve{x}}^{T}w$，这实际上等价于

4 EXPERIMENTAL RESULTS

In this section, we evaluate the performance of DCN on some popular classification datasets.

4.1 Criteo Display Ads Data

The Criteo Display Ads dataset is for the purpose of predicting ads click-through rate. It has 13 integer features and 26 categorical features where each category has a high cardinality. For this dataset, an improvement of 0.001 in logloss is considered as practically significant. When considering a large user base, a small improvement in prediction accuracy can potentially lead to a large increase in a company’s revenue. The data contains 11 GB user logs from a period of 7 days (∼41 million records). We used the data of the first 6 days for training, and randomly split day 7 data into validation and test sets of equal size.

4 实验结果

本节中，我们在一些主流分类数据集上评估了DCN的效果。

4.1 Criteo广告展现数据

Criteo展示广告的数据集是为了预测广告点击率，它有13个整数特征和26个分类特征，每个类别都有很高的基数。在这个数据集上，logloss具有0.001的提升都具有实际意义，当考虑到大量的用户群时，预测精度的微小提高可能会导致公司收入的大幅度增加。数据包含7天11 GB的用户日志（约4100万记录）。我们使用前6天的数据进行培训，并将第7天的数据随机分成相等大小的验证和测试集

4.2 Implementation Details

DCN is implemented on TensorFlow, we briefly discuss some implementation details for training with DCN.
$Dataprocessingandembedding.$ Real-valued features are normalized by applying a log transform. For categorical features, we embed the features in dense vectors of dimension $6\times (categorycardinality{)}^{\frac{1}{4}}$. Concatenating all embeddings results in a vector of dimension 1026.
$Optimization.$ We applied mini-batch stochastic optimization with Adam optimizer [9]. The batch size is set at 512. Batch normalization [6] was applied to the deep network and gradient clip norm was set at 100.
Regularization. We used early stopping, as we did not find $L_2$ regularization or dropout to be effective.
$Hyperparameters.$ We report results based on a grid search over the number of hidden layers, hidden layer size, initial learning rate and number of cross layers. The number of hidden layers ranged from 2 to 5, with hidden layer sizes from 32 to 1024. For DCN, the number of cross layers is from 1 to 6. e initial learning rate4 was tuned from 0.0001 to 0.001 with increments of 0.0001. All experiments applied early stopping at training step 150,000, beyond which overfitting started to occur.

4.2 实施详细

DCN在Tensorflow上实现，我们简要讨论DCN的一些实现细节。
数据处理与嵌入。实值特性通过应用对数变换进行标准化。对于分类特征，我们嵌入密集向量的特征维度：$6\times （类别基数{）}^{\frac{1}{4}}$。在一个1026维的向量连接所有嵌入的结果。
优化。我们使用Adam优化器进行小批量随机优化，batch size设置为512，在深度网络中设置批标准化，梯度剪切标准化设置为100。
正则化。使用早停止，因为我们发现$L_2$ 正则或使用dropout并没有效果。
超参数。我们展示了基于网格搜索的隐藏层数量、隐藏层大小、初始学习速率和跨层层数等结果。隐藏层的数量从2到5不等，隐藏层大小从32到1024。DCN，交叉层数从1到6。初始学习率进行了调整，从0.0001到0.001，增量为0.0001。所有的实验应用早期停止训练的150000步，超过150000就会出现过拟合。

4.3 Models for Comparisons

We compare DCN with five models: the DCN model with no cross network (DNN), logistic regression (LR), Factorization Machines (FMs), Wide and Deep Model (W&D), and Deep Crossing (DC).
$DNN.$ The embedding layer, the output layer, and the hyperparameter tuning process are the same as DCN. The only change from the DCN model was that there are no cross layers.
$LR.$ We used Sibyl [2]—a large-scale machine-learning system for distributed logistic regression. The integer features were discretized on a log scale. The cross features were selected by a sophisticated feature selection tool. All of the single features were used.
$FM.$ We used an FM-based model with proprietary details.
$W$&$D.$ Different than DCN, its wide component takes as input raw sparse features, and relies on exhaustive searching and domain knowledge to select predictive cross features. We skipped the com- parison as no good method is known to select cross features.
$DC.$ Compared to DCN, DC does not form explicit cross features. It mainly relies on stacking and residual units to create implicit crossings. We applied the same embedding (stacking) layer as DCN, followed by another ReLu layer to generate input to a sequence of residual units. The number of residual units was tuned form 1 to 5, with input dimension and cross dimension from 100 to 1026.

4.3 模型比较

我们将DCN和以下5中模型进行比较：不带交叉网络的DCN结构（DNN）、逻辑回归（LR）、因子机（FMs）、宽而深模型（W&D）、深度交叉模型（DC）。
深度神经网络。嵌入层、输出层和超参数微调过程与DCN相同。唯一的变化是没有交叉层。
逻辑回归。我们用Sybil[ 2 ] ——一种大规模机器学习系统实现的分布式逻辑回归。在对数刻度上离散整数特征。交叉特征是由一个复杂的特征选择工具选择的，所有的单一功能都被使用了。
因子机。我们使用基于FM的模型，具有专有的细节。
W&D。不同于DCN，其广泛的组件需要输入原始稀疏的特点，以及依赖于遍历搜索和选择预测跨领域知识的特点。我们跳过了比较，因为没有已知好的方法来选择交叉特征。
DC。相比于DCN，DC并没有形成明确的交叉特征。它主要依靠堆叠和残差单位来创建隐式交叉点。我们采用相同的嵌入（堆叠）层的DCN，紧接着又热鲁层生成输入序列的残差单元。剩余单元数从1到5调整，输入尺寸和交叉尺寸从100到1026。

4.4 Model Performance

In this section, we first list the best performance of different models in logloss, then we compare DCN with DNN in detail, that is, we investigate further into the effects introduced by the cross network.

Performance of different models. Th e best test logloss of different models are listed in Table 1. The optimal hyperparameter settings were 2 deep layers of size 1024 and 6 cross layers for the DCN model, 5 deep layers of size 1024 for the DNN, 5 residual units with input dimension 424 and cross dimension 537 for the DC, and 42 cross features for the LR model. That the best performance was found with the deepest cross architecture suggests that the higher-order feature interactions from the cross network are valuable. As we can see, DCN outperforms all the other models by a large amount. In particular, it outperforms the state-of-art DNN model but uses only 40% of the memory consumed in DNN.

For the optimal hyperparameter setting of each model, we also report the mean and standard deviation of the test logloss out of 10 independent runs: DCN: 0.4422 ± 9 × 10−5, DNN: 0.4430 ± 3.7 × 10−4, DC: 0.4430 ± 4.3 × 10−4. As can be seen, DCN consistently outperforms other models by a large amount.

Comparisons Between DCN and DNN. Considering that the cross network only introduces $O(d)$ extra parameters, we compare DCN to its deep network—a traditional DNN, and present the experimental results while varying memory budget and loss tolerance.

In the following, the loss for a certain number of parameters is reported as the best validation loss among all the learning rates and model structures. The number of parameters in the embedding layer was omitted in our calculation as it is identical to both models.
Table 2 reports the minimal number of parameters needed to achieve a desired logloss threshold. From Table 2, we see that DCN is nearly an order of magnitude more memory efficient than a single DNN, thanks to the cross network which is able to learn bounded-degree feature interactions more efficiently.

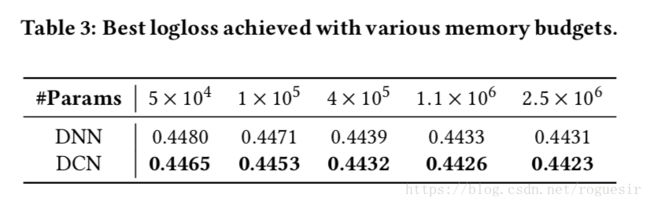
Table 3 compares performance of the neural models subject to fixed memory budgets. As we can see, DCN consistently outperforms DNN. In the small-parameter regime, the number of parameters in the cross network is comparable to that in the deep network, and the clear improvement indicates that the cross network is more efficient in learning effective feature interactions. In the large-parameter regime, the DNN closes some of the gap; however, DCN still outperforms DNN by a large amount, suggesting that it can efficiently learn some types of meaningful feature interactions that even a huge DNN model cannot.

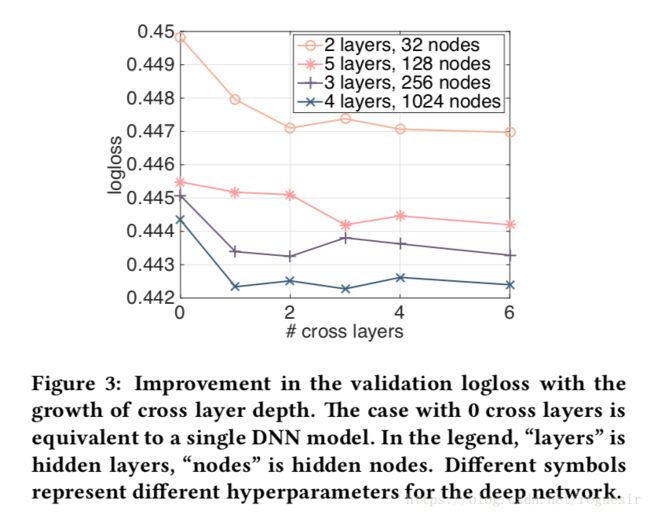
We analyze DCN in finer detail by illustrating the effect from introducing a cross network to a given DNN model. We first compare the best performance of DNN with that of DCN under the same number of layers and layer size, and then for each setting, we show how the validation logloss changes as more cross layers are added. Table 4 shows the differences between the DCN and DNN model in logloss. Under the same experimental se ing, the best logloss from the DCN model consistently outperforms that from a single DNN model of the same structure. That the improvement is consistent for all the hyperparameters has mitigated the randomness effect from the initialization and stochastic optimization.

Figure 3 shows the improvement as we increase the number of cross layers on randomly selected settings. For the deep networks in Figure 3, there is a clear improvement when 1 cross layer is added to the model. As more cross layers are introduced, for some settings the logloss continues to decrease, indicating the introduced cross terms are effective in the prediction; whereas for others the logloss starts to fluctuate and even slightly increase, which indicates the higher-degree feature interactions introduced are not helpful.

4.4 模型表现

在这一部分中，我们首先列出不同模型的最佳性能LogLoss，然后比较DCN DNN的细节，这是我们进一步研究的交叉网络引入的影响。
不同模型的表现。不同模型的最佳测试log损失列于表1，优化超参数设置为：DCN：两个尺寸为1024的深度层和6个交叉层；DNN为5个尺寸为1024的深度层；DC为带有输入维度为424的5个残差单元和537个交叉维度；逻辑回归有42个交叉特征。发现最优秀的性能与最深刻的交叉架构表明，高阶特征相互作用的交叉网络是有价值的。我们可以看到，DCN优于所有其他模型。特别是，它优于现有的DNN模型的状态但是相比于DNN只有40%的内存消耗。

对于每个模型的最优参数设置：10个独立运行测试log损失的标准差：DCN：$0.4422\pm 9\times 10^{-5}$，DNN：$0.4430\pm 3.7\times 10^{-4}$，DC： $0.4430\pm 4.3\times 10^{-4}$，可以看出，DCN大幅优于其他模型。
DCN和DNN间的比较。考虑到DCN仅仅介绍$O(d)$ 以外的其他参数，对比DCN中的深度网络，——一个普通的深度神经网络，给出了不同记忆预算和损失容忍度下的实验结果。
在下面,损失一定数量的参数报告为是最好的验证损失在所有学习率和模型结构。在嵌入层参数的数量是忽略了在我们的计算模型是相同的。
表2报告所需的最少数量的参数来实现所需的logloss阈值。从表2中,我们看到宽带近一个数量级更多的内存效率比单一款,由于交叉网络能够学习bounded-degree功能更有效地交互。

表3比较了神经模型的性能受固定内存预算。我们可以看到,DCN一直优于DNN。少的参数,交叉网络参数的数量是相媲美,在深层网络,和明显改善表明交叉网络更有效的学习有效的特征交互。大规模参数,接近一些DNN的差距;然而,DCN仍然优于由大量款,这表明它可以有效地学习一些类型的有意义的交互特性,即使是一个巨大的DNN模型也不能实现。

我们分析DCN在更多的细节说明效果从交叉网络某一个DNN模型。我们首先比较DNN的最佳性能与DCN在相同层数和层大小,然后为每个设置,我们展示如何验证logloss随着越来越多的交叉层的变化。表4显示了在DCN的logloss和DNN模型之间的差异。在同样实验设置下,从DCN中获得的最好的logloss始终优于具有相同结构的单一DNN模型。对于所有超参数，这种提升减轻了随机性效应的初始化和随机优化。

图3显示了改进我们增加交叉层随机选择设置。深层网络在图3中,有明显的改善,当1交叉层添加到模型中。随着越来越多的跨层介绍了,对于一些设置logloss继续减少,表明引入交叉项预测是有效的;为别人而logloss开始波动,甚至略有增加,这表明摘要特性相互作用引入并不有用。

4.5 Non-CTR datasets

We show that DCN performs well on non-CTR prediction problems. We used the forest cover type (581012 samples and 54 features) and Higgs (11M samples and 28 features) datasets from the UCI repository. The datasets were randomly split into training (90%) and testing (10%) set. A grid search over the hyperparameters was performed. The number of deep layers ranged from 1 to 10 with layer size from 50 to 300. The number of cross layers ranged from 4 to 10. The number of residual units ranged from 1 to 5 with their input dimension and cross dimension from 50 to 300. For DCN, the input vector was fed to the cross network directly.

For the forest covertype data, DCN achieved the best test accuracy 0.9740 with the least memory consumption. Both DNN and DC achieved 0.9737. The optimal hyperparameter settings were 8 cross layers of size 54 and 6 deep layers of size 292 for DCN, 7 deep layers of size 292 for DNN, and 4 residual units with input dimension 271 and cross dimension 287 for DC.

4.5 NON-CTR数据集

我们表明,DCN执行non-CTR预测问题。我们使用了森林覆盖类型(581012样品和54特性)和希格斯粒子(11M样本和28个特征)的UCI数据集的存储库。数据集被随机分成训练(90%)和测试(10%)，执行超参数网格搜索。深层的数量范围从1到10层大小从50到300。跨层的数量从4到10不等。剩余的数量单位范围从1到5的输入维度和跨维度从50到300。对DCN输入向量直接输入到交叉网络。
森林覆盖类型数据,宽带实现最好的测试精度0.9740最少的内存消耗。款和直流0.9737实现。最优hyperparameter设置8交叉54层的大小和尺寸的深层,DCN是292大小的深层,292款,4剩余单位输入维271年和287年跨维度。
For the Higgs data, DCN achieved the best test logloss 0.4494, whereas DNN achieved 0.4506. The optimal hyperparameter set- tings were 4 cross layers of size 28 and 4 deep layers of size 209 for DCN, and 10 deep layers of size 196 for DNN. DCN outperforms DNN with half of the memory used in DNN.
希格斯粒子数据、DCN实现最好的测试logloss 0.4494,而达到0.4506DNN。最优超参数设置——东4跨层大小28日和4的深层,大小209DCN,和10的深层,大小为196DNN。DCN优于同款DNN使用的内存的一半。

5 CONCLUSION AND FUTURE DIRECTIONS

Identifying effective feature interactions has been the key to the success of many prediction models. Regrettably, the process often requires manual feature crating and exhaustive searching. DNNs are popular for automatic feature learning; however, the features learned are implicit and highly nonlinear, and the network could be unnecessarily large and inefficient in learning certain features. The Deep & Cross Network proposed in this paper can handle a large set of sparse and dense features, and learns explicit cross features of bounded degree jointly with traditional deep representations. The degree of cross features increases by one at each cross layer. Our experimental results have demonstrated its superiority over the state-of-art algorithms on both sparse and dense datasets, in terms of both model accuracy and memory usage.
We would like to further explore using cross layers as building blocks in other models, enable effective training for deeper cross networks, investigate the efficiency of the cross network in polynomial approximation, and better understand its interaction with deep networks during optimization.

结论和未来方向

识别有效特征相互作用一直是许多预测模型成功的关键。遗憾的是,这个过程通常需要人工装箱和详尽的搜索功能。DNN很流行的自动学习功能;然而,学习是隐式和高度非线性的特性,和网络可以在学习某些特性过于庞大,效率低下。深度交叉网络提出了可以处理大量的稀疏和密集的特性,和显式有限程度的交叉特征共同学习与传统深表示。交叉功能的程度在每个交叉层增加了一个。我们的实验结果证明其优越性在图象处理稀疏和密集的数据集,在模型精度和内存使用。我们想进一步探索在其他模型使用交叉层作为构建块,使有效的更深层次的交叉训练网络,调查在多项式近似交叉网络的效率,和更好地理解其与深度互动网络优化。

• 更新时间：2019-03-18
• 注：实验结果部分翻译时候辅助参考google翻译，如果有地方与原文相差较大，请在下方评论。