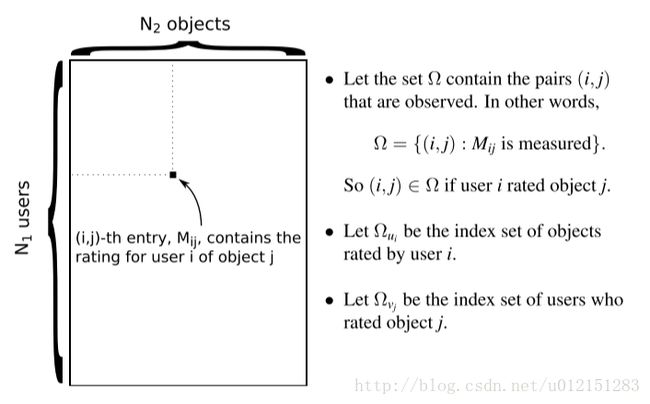
矩阵分解(MF,SVD)和协同过滤(CF)

协同过滤Collaborative Filtering

使用用户历史的行为来做未来的推荐。忽略了关于用户或item的先验信息。

• CF使用与我相似的用户的评分来预测我的评分
• CF是领域无关的，不需要知道现在在对什么评分，谁在评分，评分是多少

一种CF方法称为基于邻域的方法。例如
1. 定义一个相似度评分，基于用户之间评分的重叠度
2. 基于相似度评分，使用邻域内的评分来为我喜欢的item打分

过滤方法并不是互斥的。内容信息可以被添加到协同过滤系统来提升性能。

矩阵分解MF

SVD

我们知道矩阵的特征分解可以将矩阵分解成一组特征向量和特征值。
现在介绍另一种矩阵分解的方法，称为奇异值分解，将矩阵分解为奇异向量和奇异值。
每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这时只能用奇异值分解。
在特征分解中，我们可以将矩阵M写作 M=Vdiag(λ)V−1 。
奇异值分解中，将矩阵M分解成 M=USVT ，这里U和V都是正交矩阵，S是对角矩阵（S不一定是方阵）。
矩阵S对角线上的元素被称为矩阵M的奇异值。
矩阵U的列向量被称为左奇异向量。矩阵V的列向量被称为右奇异向量。
事实上，M的左奇异向量是 MMT 的特征向量。M的右奇异向量是 MTM （协方差矩阵）的特征向量。M的非零奇异值是 MTM 的特征值的平方根，同时也是 MMT 的特征值的平方根。
证明
对于正交矩阵有 A−1=AT
MMTU=USVTVSTUT=US2=S2U ，所以U的列向量是 MMT 的特征向量。

SVD应用

　SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。下面我们就对SVD用于PCA降维做一个介绍。

SVD用于PCA

PCA中，需要找到样本协方差矩阵 XTX 的最大的d个特征向量，当样本数和特征数量很多时，计算量很大。
事实上，SVD也可以得到 XTX 的最大的d个特征向量构成的矩阵，但是一些SVD算法（查查哪些）可以不用先求出协方差矩阵 XTX ，就可以求出右奇异矩阵 V 。
这样就可以通过SVD分解来完成PCA算法，这个方法在样本量很大的时候很有效。
PCA仅仅使用了SVD的右奇异矩阵，左奇异矩阵可以用于行的压缩。
右奇异矩阵用于列即特征的压缩，即PCA降维。

SVD矩阵分解

根据奇异值分解SVD
Mn×d=Un×rSr×rVTr×d
其中 UTU=i,VTV=I,S是对角矩阵,Sii≥0
r=rank(M)
我们将定义模型来学习矩阵M的低秩分解，能够
1. 处理M存在大部分缺失值的问题
2. 低秩 d<<min(N1,N2)(e.g.,d≈10)
3. 学习user i和 item j的向量表示

为什么学习一个低秩矩阵？

1. 评分矩阵的许多列是相似的
2. 低秩意味着 N1 维的列并不能填充满整个 N1 空间
3. 由于95%以上的数据可能缺失，低秩的限制让我们有可能根据相关性填充数据

概率矩阵分解PMF

生成模型

对 N1 个用户和 N2 个物体,生成向量：

μi∼N(0,λ−1I),i=1,...,N1vj∼N(0,λ−1I),j=1,...,N2

根据以上向量评分数据的分布为
Mij∼N(uTivj,σ2)for each(i,j)∈Ω
备注
- 由于 Mij 是评分，高斯假设显然是错误的（高斯假设评分取值范围为所有实数，而一般评分为非负整数）
- 但是，高斯是一个方便的假设。算法实现容易，模型也可正常工作

模型推断

最大后验概率MAP

对数似然函数和MAP
UMAP,VMAP=argmaxU,V∑(i,j)∈Ωlnp(Mij|ui,vj)+∑i=1N1lnp(ui)+∑j=1N2lnp(vj)
记MAP的目标函数为L，我们希望最大化:
L=−∑(i,j)∈Ω12σ2||Mij−uTivj||2−∑i=1N1λ2||ui||2−∑j=1N2λ2||vj||2+constant
平方项的产生源于参数服从高斯分布。
求L对参数的偏导数，并令其为0

∇uiL=∑j∈Ωui1σ2(Mij−uTivj)vj−λui=0∇vjL=∑i∈Ωvj1σ2(Mij−vTjui)ui−λvj=0

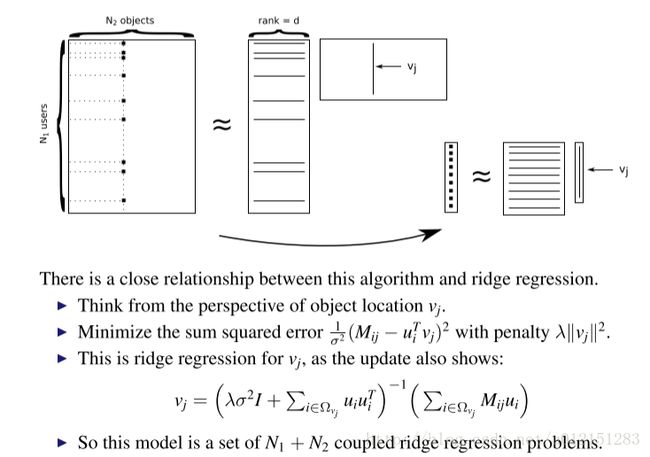
我们可以独立地求解 ui 和 vj （因此不需要EM算法）

uivj=(λσ2I+∑j∈ΩuivjvTj)−1(∑j∈ΩuiMijvj)=(λσ2I+∑j∈ΩvjuiuTi)−1(∑j∈ΩvjMijui)

注意，我们不能一次性将所有的 ui 和 vj 求解。
因此，采用类似K-menas和GMM的 坐标下降算法。

矩阵分解和Ridge回归

参考资料

奇异值分解(SVD)原理与在降维中的应用