转自:http://www.cnblogs.com/BitArt/archive/2012/12/26/2833100.html
1.概述
CRC即Cyclic Redundancy Check,循环冗余校验,是一种数字通信中的常用信道编码技术。其特征是信息段和校验字段的长度可以任意选定。
2.CRC校验的基本原理:
CRC码是由两部分组成的,前部分是信息码,就是需要校验的信息,后部分是校验码,如果CRC码长共n bit,信息码长k bit,就称为(n,k)码,剩余的r bit即为校验位。如:(7,3)码:110 1001,前三位110为信息码,1001为校验码。
3.校验码的生成规则:
1)将原信息码左移r bit,右侧补零,如 110--> 110 0000;
2)用110 0000除以g(x) (注意,使用的是模2除法,见下文),得到的余数即为CRC校验码;
3)将校验码续接到信息码的尾部,形成CRC码。
4.关于生成多项式g(x)
在产生CRC校验码时,要用到除法运算,一般来说,这是比较麻烦的,因此,把二进制信息预先转换成一定的格式,这就是CRC的多项式表示。二进制数表示为生成多项式的系数,如下:
![]()
所有二进制数均被表示为一个多项式,x仅是码元位置的标记,因此我们并不关心x的取值,称之为码多项式。(我没研究过CRC代数推理过程,没体会到用多项式计算的方便之处,这里要学会的就是给出生成多项式g(x),能写出对应的二进制即可)
常见的生成多项式如下:
5.关于模2除法
模2运算就是加法不考虑进位,减法不考虑借位,
1)加法运算:
0+0=0 0+1=1 1+0=1 1+1=0
例如0101+0011=0110,列竖式计算:
0 1 0 1
+ 0 0 1 1
──────
0 1 1 0
2)减法运算:
0-0=0 0-1=1 1-0=1 1-1=0
例如0110-0011=0101,列竖式计算:
0 1 1 0
- 0 0 1 1
──────
0 1 0 1
3)乘法运算
0×0=0 0×1=0 1×0=0 1×1=1
多位二进制模2乘法类似于普通意义上的多位二进制乘法,不同之处在于后者累加中间结果时采用带进位的加法,而模2乘法对中间结果的处理方式采用的是模2加法。例如1011×101=100111,列竖式计算:
4)除法运算:
0÷1=0 1÷1=1
多位二进制模2除法也类似于普通意义上的多位二进制除法,但是在如何确定商的问题上两者采用不同的规则。后者按带借位的二进制减法,根 据余数减除数够减与否确定商1还是商0,若够减则商1,否则商0。多位模2除法采用模2减法,不带借位的二进制减法,因此考虑余数够减除数与否是没有意义 的。实际上,在CRC运算中,总能保证除数的首位为1,则模2除法运算的商是由余数首位与除数首位的模2除法运算结果确定。因为除数首位总是1,按照模2 除法运算法则,那么余数首位是1就商1,是0就商0。例如1100100÷1011=1110……110,列竖式计算:
掌握了上面的运算规则,您可以尝试计算一个复杂一点的,如下:
如果您得到的余数结果正确,您掌握的东西就够用了。
6.CRC-CCITT的硬件实现
CRC-CCITT的生成多项式为:
对应的二进制数就是上面复杂运算中那个除数。由刚才的计算可知,对于8 bit的数据 0xaa,它的CRC校验码为0001 0100 1010 0000,下面用verilog来实现,看能否得到这个结果:
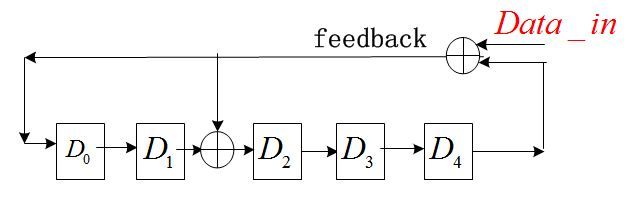
要实现这一过程,仍然需要LFSR电路,参看《FPGA产生基于LFSR的伪随机数》中关于该电路特性的介绍,如果您不需要了解原理,直接略过即可;有所改进的地方就是,可以将伪随机数发生器看作一个Moore型状态机,它的输出只与当前的状态有关;而此时利用LFSR电路,需要引入数据输入端,输出不仅取决于当前的状态,还取决于输入信号,相当于Mealy型状态机,如下图:
![]()
注意对比与伪随机数产生器中该反馈支路的区别!
反馈项gr+1gr……g0为生成多项式的系数,依然是1代表存在反馈,0代表不存在反馈;此电路可以完成上述的模2除法操作,若我们要求0xaa的CRC校验码,则从高位到低位顺序输入0xaa共8 bit后,D15……D0中的数据即为所要求的余数,即CRC校验位。
7.verilog描述
如果用时序电路串行实现,则8 bit数据要移位8次,就需要8个clk,效率低下,为了能在一个时钟周期输出结果,必须采用组合电路,当然,这是以空间换时间的方法,由于使用了for循环8次,直观的讲电路规模将扩大8倍。。。
module CRC_GEN(
input rst, /*async reset,active low*/
input clk, /*clock input*/
input [7:0] data_in, /*parallel data input pins */
input d_valid, /* data valid,start to generate CRC, active high*/
output reg[15:0] crc
);
integer i;
reg feedback;
reg [15:0] crc_tmp;
/*
* sequential process
*/
always @(posedge clk or negedge rst)
begin
if(!rst)
crc <= 16'b0; /*触发器中的初始值十分重要 */
else if(d_valid==1'b0)
crc <= 16'b0;
else
crc <= crc_tmp;
end
/*
* combination process
*/
always@( data_in or crc)
begin
crc_tmp = crc;
for(i=7; i>=0; i=i-1)
begin
feedback = crc_tmp[15] ^ data_in[i];
crc_tmp[15] = crc_tmp[14];
crc_tmp[14] = crc_tmp[13];
crc_tmp[13] = crc_tmp[12];
crc_tmp[12] = crc_tmp[11] ^ feedback;
crc_tmp[11] = crc_tmp[10] ;
crc_tmp[10] = crc_tmp[9];
crc_tmp[9] = crc_tmp[8];
crc_tmp[8] = crc_tmp[7];
crc_tmp[7] = crc_tmp[6];
crc_tmp[6] = crc_tmp[5];
crc_tmp[5] = crc_tmp[4] ^ feedback;
crc_tmp[4] = crc_tmp[3];
crc_tmp[3] = crc_tmp[2];
crc_tmp[2] = crc_tmp[1];
crc_tmp[1] = crc_tmp[0];
crc_tmp[0] = feedback;
end
end
endmodule
仿真结果如下:得到的是数据0xaa和0xf0的CRC校验码,为验证结果的正确性,您可以按照模2法则手工计算一下^.^
8.同样给出一个4 bit信息位,5 bitCRC码的(9,4)码的程序和仿真结果,程序的流程与上述流程完全一样:
module CRC5_GEN(
input rst,
input clk,
input [3:0] data_in,
input d_valid,
output reg[4:0] crc
);
integer i;
reg feedback;
reg [4:0] crc_tmp;
always @(posedge clk or negedge rst)
begin
if(!rst)
crc <= 5'b0;
else if(d_valid==1'b0)
crc <= 5'b0;
else
crc <= crc_tmp;
end
always@( data_in or crc)
begin
crc_tmp = crc;
for(i=3; i>=0; i=i-1)
begin
feedback = crc_tmp[4] ^ data_in[i];
crc_tmp[4] = crc_tmp[3];
crc_tmp[3] = crc_tmp[2];
crc_tmp[2] = crc_tmp[1] ^ feedback;
crc_tmp[1] = crc_tmp[0];
crc_tmp[0] = feedback;
end
end
endmodule
后记:细心的读者可能发现,博主对LFSR电路能完成模2求余操作的原因避而不谈,不是因为不告诉您,是因为博主也不是很清楚,工科背景对数学推理实在是有点不知所云,尤其是看到国内教材那好几页的公式的时候…………如果您有深入浅出的讲解LFSR电路由来与应用的文章,注意是深入浅出的,请您为博主推荐,在此感谢!