习题集解析部分
第2章 线性表
——《数据结构题集》-严蔚敏.吴伟民版
源码使用说明 链接☛☛☛ 《数据结构-C语言版》(严蔚敏,吴伟民版)课本源码+习题集解析使用说明
课本源码合辑 链接☛☛☛ 《数据结构》课本源码合辑
习题集全解析 链接☛☛☛ 《数据结构题集》习题解析合辑
相关测试数据下载 链接☛ 数据包
本习题文档的存放目录:数据结构\▼配套习题解析\▼02 线性表
文档中源码的存放目录:数据结构\▼配套习题解析\▼02 线性表\▼习题测试文档-02
源码测试数据存放目录:数据结构\▼配套习题解析\▼02 线性表\▼习题测试文档-02\Data
一、基础知识题
2.1❶描述以下三个概念的区别:头指针,头结点,首元结点(第一个元素结点)。
2.2❶填空题
(1)在顺序表中插入或删除一个元素,需要平均移动 表中一半 元素,具体移动的元素个数与 该元素的位置 有关。
(2)顺序表中逻辑上相邻的元素的物理位置 必定 相邻。单链表中逻辑上相邻的元素在物理位置 不一定 相邻。
(3)在单链表中,除了首元结点外,任一结点的存储位置由 其直接前驱结点的链域的值 指示。
(4)在单链表中设置头结点的作用是 插入和删除首元素时不必进行特殊处理 。
2.3❷在什么情况下用顺序表比链表好?
![]()
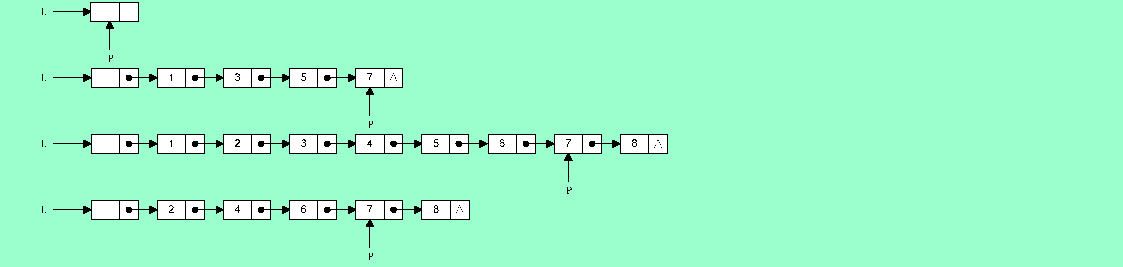
2.4❶对以下单链表分别执行下列各程序段,并画出结果示意图。
(1)Q=P->next;
(2)L=P->next;
(3)R->data=P->data;
(4)R->data=P->next->data;
(5)P->next->next->next->data=P->data;
(6)T=P;
while(T!=NULL)
{
T->data=T->data*2;
T=T->next;
}
(7)T=P;
while(T->next!=NULL)
{
T->data=T->data*2;
T=T->next;
}
2.5❶画出执行下列各行语句后各指针及链表的示意图。
L = (LinkList) malloc (sizeof(LNode));
P = L;
for(i=1; i<=4; i++)
{
P->next= (LinkList) malloc (sizeof(LNode));
P = P->next;
P->data = i*2-1;
}
P->next = NULL;
for(i=4; i>=1; i--)
Ins_LinkList(L, i+1, i*2);
for(i=1; i<=3; i++)
Del_LinkList(L, i);
2.6❷已知L是无表头结点的单链表,且P结点既不是首元结点,也不是尾元结点,试从下列提供的答案中选择合适的语句序列。
a.在P结点后插入S结点的语句序列是 (4)(1) 。
b.在P结点前插入S结点的语句序列是 (7)(11)(8)(4)(1) 。
c.在表首插入S结点的语句序列是 (5)(12) 。
d.在表尾插入S结点的语句序列是 (9)(1)(6) 。
(1)P->next=S;
(2)P->next=P->next->next;
(3)P->next=S->next;
(4)S->next=P->next;
(5)S->next=L;
(6)S->next=NULL;
(7)Q=P;
(8)while(P->next!=Q)
P=P->next;
(9)while(P->next!=NULL)
P=P->next;
(10)P=Q;
(11)P=L;
(12)L=S;
(13)L=P;
2.7❷已知L是带表头结点的非空单链表,且P结点既不是首元结点,也不是尾元结点,试从下列提供的答案中选择合适的语句序列。
a.删除P结点的直接后继结点的语句序列是 (11)(3)(14) 。
b.删除P结点的直接前驱结点的语句序列是 (10)(12)(8)(11)(3)(14) 。
c.删除P结点的语句序列是 (10)(12)(7)(3)(14) 。
d.删除首元结点的语句序列是 (12)(11)(3)(14) 。
e.删除尾元结点的语句序列是 (9)(11)(3)(14) 。
(1)P=P->next;
(2)P->next=P;
(3)P->next=P->next->next;
(4)P=P->next->next;
(5)while(P!=NULL)
P=P->next;
(6)while(Q->next!=NULL)
{
P=Q;
Q=Q->next;
}
(7)while(P->next!=Q)
P=P->next;
(8)while(P->next->next!=Q)
P=P->next;
(9)while(P->next->next!=NULL)
P=P->next;
(10)Q=P;
(11)Q=P->next;
(12)P=L;
(13)L=L->next;
(14)free(Q);
2.8❷已知P结点是某双向链表的中间结点,试从下列提供的答案中选择合适的语句序列。
注:此题答案不唯一
a.在P结点后插入S结点的语句序列是 (7)(12)(3)(6) 。
b.在P结点前插入S结点的语句序列是 (8)(13)(5)(4) 。
c.删除P结点的直接后继结点的语句序列是 (15)(1)(11)(18) 。
d.删除P结点的直接前驱结点的语句序列是 (16)(2)(10)(18) 。
e.删除P结点的语句序列是 (14)(9)(17) 。
(1)P->next=P->next->next;
(2)P->priou=P->priou->priou;
(3)P->next=S;
(4)P->priou=S;
(5)S->next=P;
(6)S->priou=P;
(7)S->next=P->next;
(8)S->priou=P-priou;
(9)P->priou->next=P->next;
(10)P->priou->next=P;
(11)P->next->priou=P;
(12)P->next->priou=S;
(13)P->priou->next=S;
(14)P->next->priou=P->priou;
(15)Q=P->next;
(16)Q=P->priou;
(17)free(P);
(18)free(Q);
2.9❷简述下列算法的功能。
(1)Status A(LinkedList L) //L是无表头结点的单链表
{
if(L&&L->next)
{
Q=L;
L=L->next;
P=L;
while(P->next)
P=P->next;
P->next=Q;
Q->next=NULL;
}
return OK;
}//A
(2)void BB(LNode *s, LNode *q)
{
p=s;
while(p->next!=q)
p=p->next;
p->next=s;
}//BB
void AA(LNode *pa, LNode *pb)
{//pa和pb分别指向单循环链表中的两个结点
BB(pa, pb);
BB(pb, pa);
}//AA
![]()
二、算法设计题
本章算法设计题设计的顺序表和线性链表的类型定义如下:
| #define LIST_INIT_SIZE 100 #define LISTINCREMENT 10 typedef struct { ElemType *elem; //存储空间基址 int length; //当前长度 int listsize; //当前分配的存储容量 }SqList; //顺序表类型 注:此文档中,ElemType被定义为int类型。 typedef struct LNode { ElemType data; Struct Lnode *next; }LNode, *LinkList; //线性链表类型 |
顺序表
2.10❷ 指出以下算法的错误和低效(即费时)之处,并将它改写为一个既正确又高效的算法。
Status DeleteK(SqList &a, int i, int k)
{//本过程从顺序存储结构的线性表a中删除第i个元素起的k个元素
if(i<1 || k<0 || i+k>a.length)
return INFEASIBLE; //参数不合法
else
for(count=1; count
{//删除一个元素
for(j=a.length; j>=i+1; j--)
a.elem[j-1] = a.elem[j];
a.length--;
}
return OK;
}//DeleteK
2.11❷设顺序表va中的数据元素递增有序。试写一算法,将x插入到顺序表的适当位置上,以保持该表的有序性。
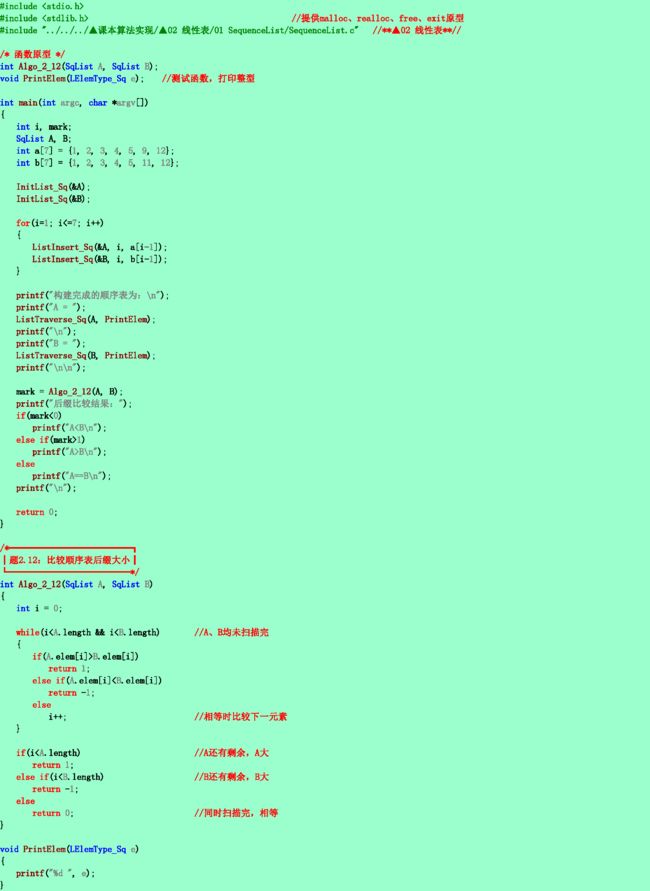
2.12❸设A=(a1,...,an)和B=(b1,...,bn)均为顺序表,A'和B'分别为A和B中除去最大共同前缀后的子表(例如,A=(x,y,y,z,x,z),B=(x,y,y,z,y,x,x,z),则两者中最大的共同前缀为(x,y,y,z),在两表中除去最大共同前缀后的子表分别为A'=(x,z)和B'=(y,x,x,z))。若A'=B'=空表,则A=B;若A'=空表,而B'≠空表,或者两者均不为空表,且A'的首元小于B'的首元,则A
单链表
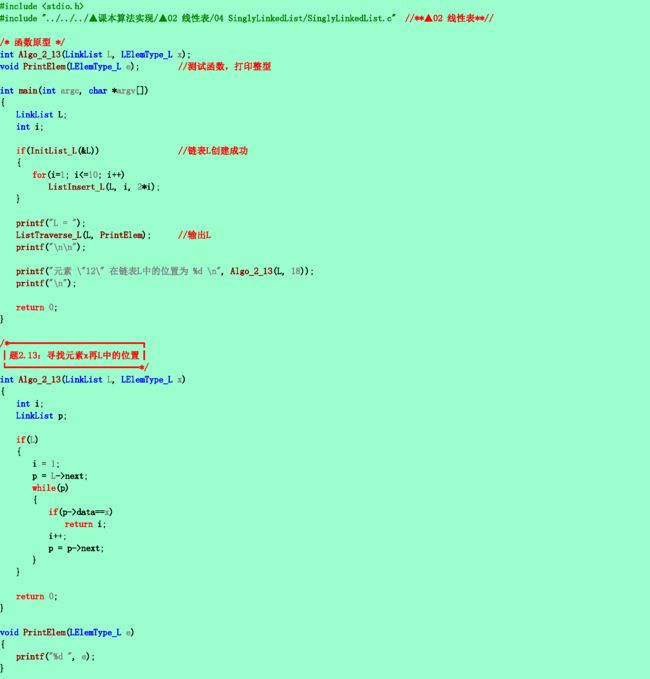
2.13❷试写一算法在带头结点的单链表结构上实现线性表操作LOCATE(L,X)。
2.14❷试写一算法在带头结点的单链表结构上实现线性表操作LENGTH(L)。
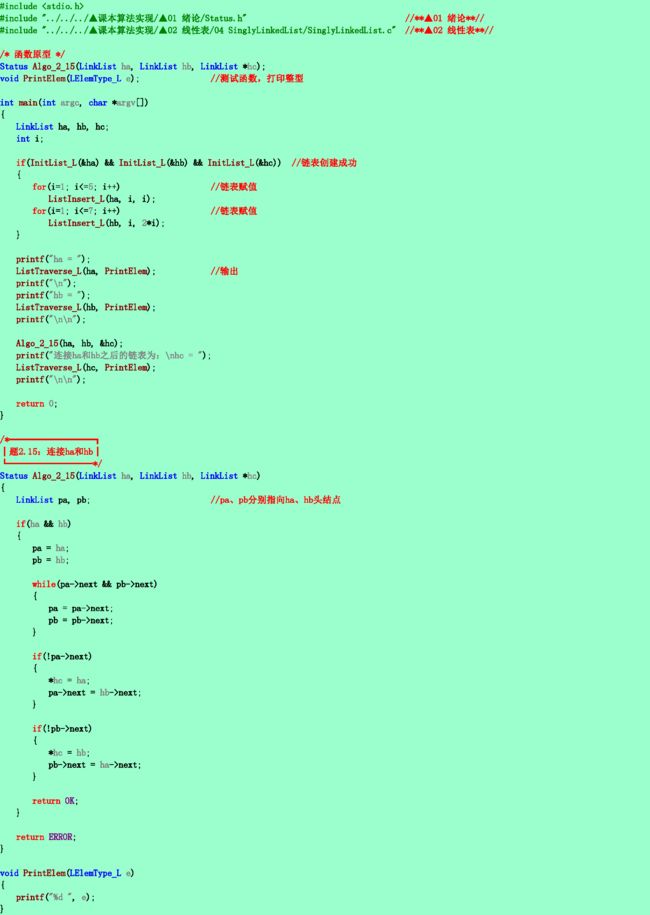
2.15❷已知指针ha和hb分别指向两个单链表的头结点,并且已知两个链表的长度分别为m和n。试写一算法将这两个链表连接在一起(即令其中一个表的首元结点连在另一个表的最后一个结点之后),假设指针hc指向连接后的链表的头结点,并要求算法以尽可能短的时间完成连接运算。请分析你的算法和时间复杂度。
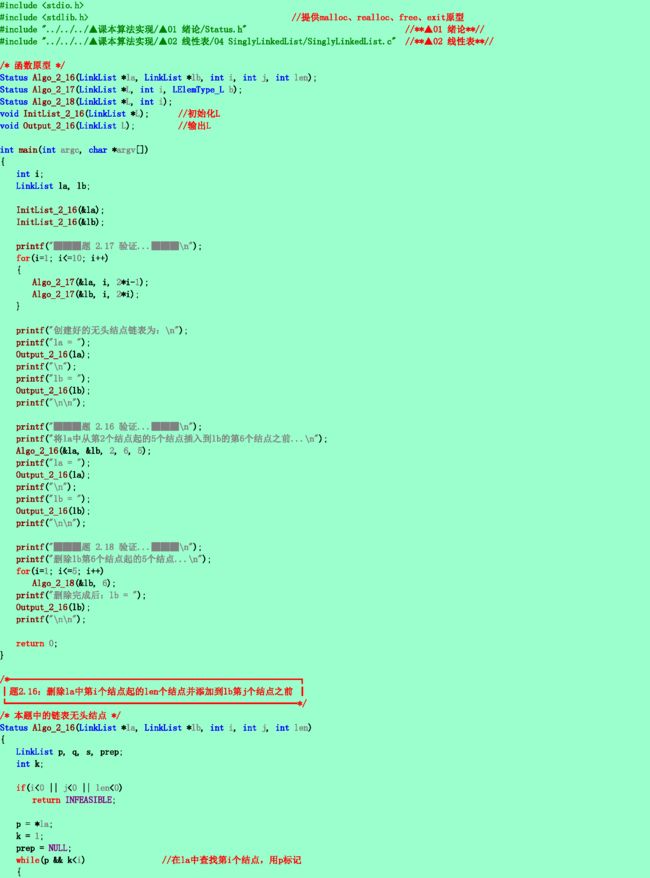
2.16❸已知指针la和lb分别指向两个无头结点单链表中的首元结点。下列算法是从表la中删除自第i个元素起共len个元素后,将它们插入到表lb中的第j个元素之前。试问此算法是否正确?如有错,则请改正之。
Status DeleteAndInsertSub (LinkedList la, LinkedList lb,int i, int j, int len)
{
if(i<0 || j<0 || len<0)
return INFEASIBLE;
p=la; k=1;
while(k
{
p=p->next;
k++;
}
q=p;
while(k<=len)
{
q=q->next;
k++;
}
s=lb;
k=1;
while(k
{
s=s->next;
k++;
}
s->next=p;
q->next=s->next;
return OK;
}//DeleteAndInsertSub
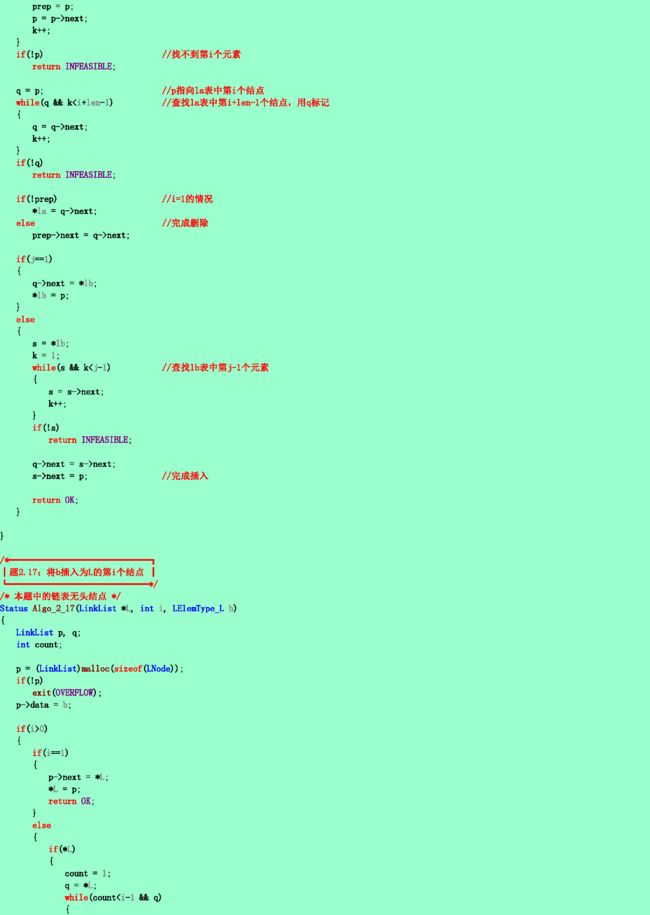
2.17❷试写一算法,在无头结点的动态单链表上实现线性表操作INSERT(L, i, b),并和在带头结点的动态单链表上实现相同操作的算法进行比较。
2.18❷同2.17题要求。试写一算法,实现线性表操作DELETE(L, i)。
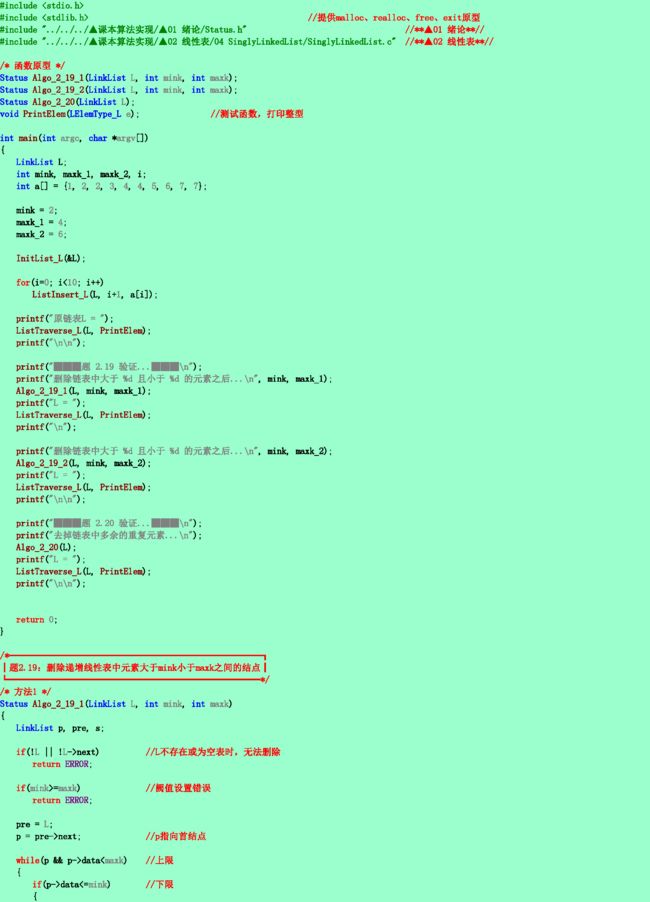
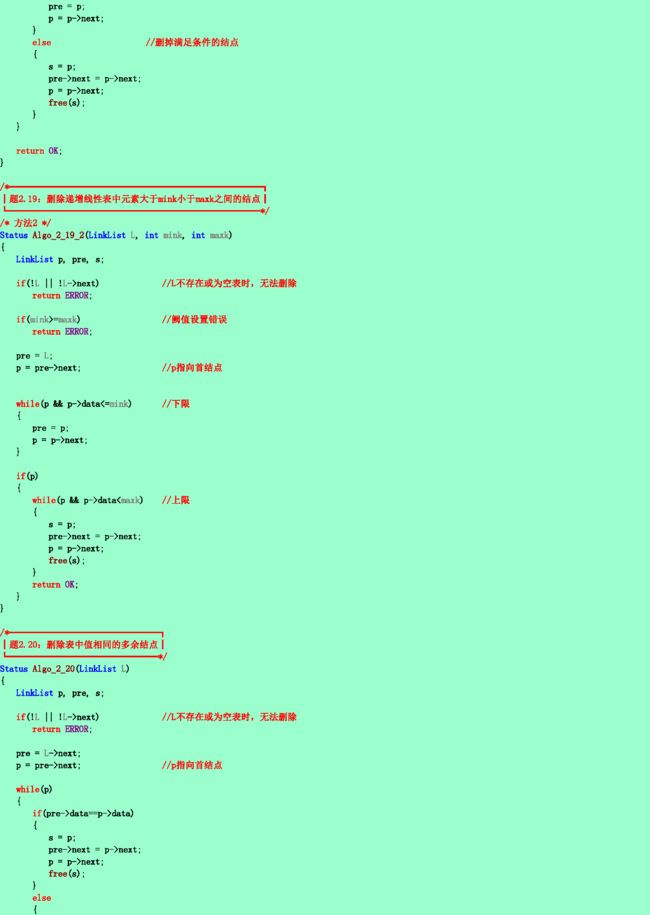
2.19❸ 已知线性表中的元素以值递增有序排列,并以单链表作存储结构。试写一高效的算法,删除表中所有值大于mink且小于maxk的元素(若表中存在这样的元素),同时释放被删结点空间,并分析你的算法的时间复杂度(注意:mink和maxk是给定的两个参变量,它们的值可以和表中的元素相同,也可以不同)。
![]()
2.20❷ 同2.19题条件(递增有序排列),试写一高效的算法,删除表中所有值相同的多余元素(使得操作后的线性表中所有元素的值均不相同),同时释放被删结点空间,并分析你的算法的时间复杂度。
顺序表
2.21❸ 试写一算法,实现顺序表的就地逆置,即利用原表的存储空间将线性表(a1, a2, ..., an)逆置为(an, an-1, ..., a1)。
单链表
2.22❸ 试写一算法,对单链表实现就地逆置。
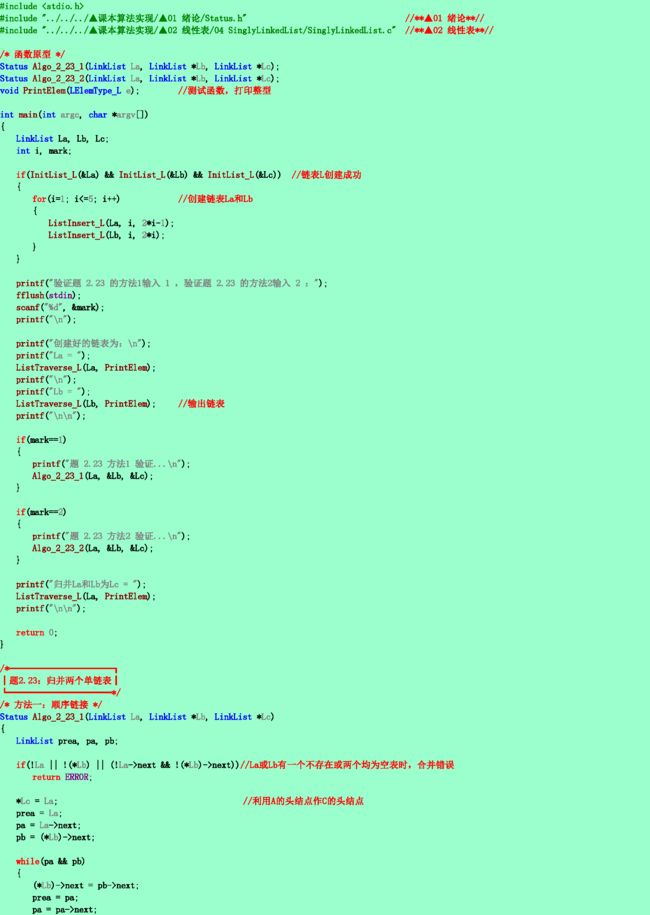
2.23❸ 设线性表A=(a1, a2, ..., am),B=(b1, b2, ..., bn),试写一个按下列规则合并A,B为线性表C的算法,即使得
C=(a1, b1, ..., am, bm, bm+1, ..., bn) 当m<=n时;
或者 C=(a1, b1, ..., an, bn, an+1, ..., am) 当m>n时。
线性表A,B和C均以单链表作存储结构,且C表利用A表和B表中的结点空间构成。注意:单链表的长度值m和n均未显式存储。
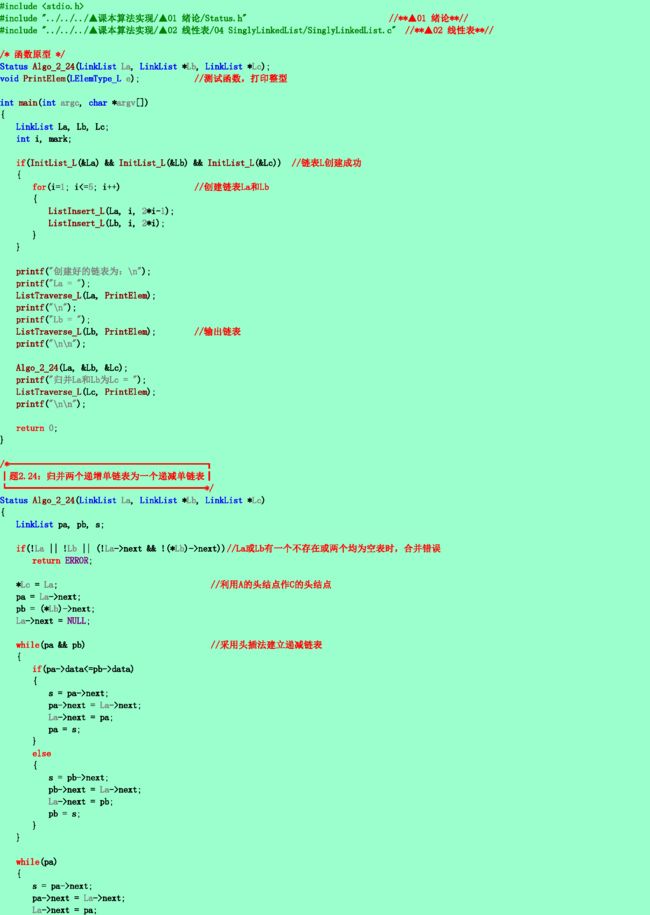
2.24❹ 假设有两个按元素值递增有序排列的线性表A和B,均以单链表作存储结构,请编写算法将A表和B表归并成一个按元素值递减有序(即非递增有序,允许表中含有值相同的元素)排列的线性表C,并要求利用原表(即A表和B表)的结点空间构造C表。
顺序表
2.25❹ 假设以两个元素依值递增有序排列的线性表A和B分别表示两个集合(即同一表中的元素值各不相同),现要求另辟空间构成一个线性表C,其元素为A和B中元素的交集,且表C中的元素也依值递增有序排列。试对顺序表编写求C的算法。
单链表
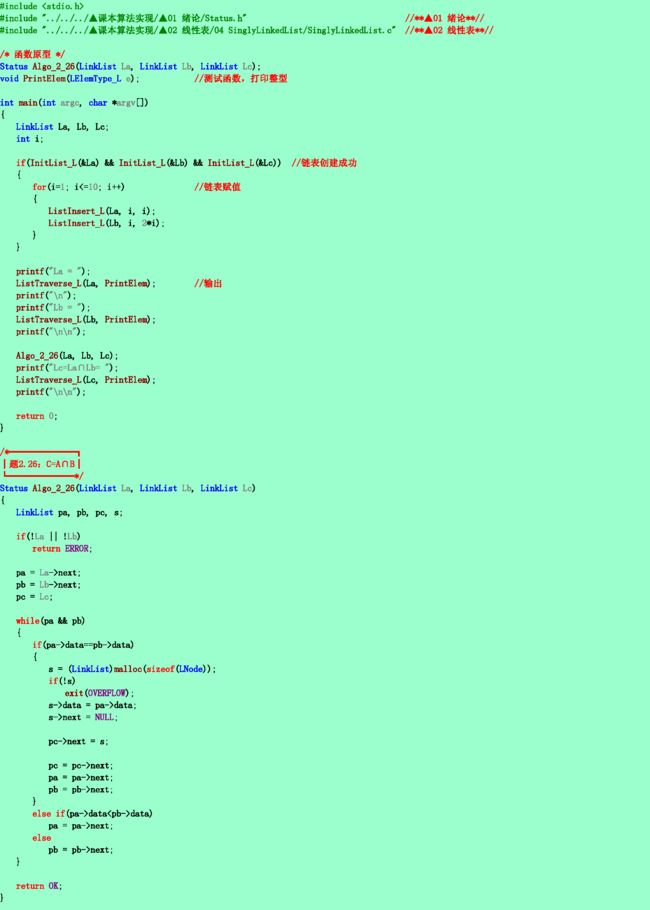
2.26❹ 要求同2.25题。试对单链表编写求C的算法。
顺序表
2.27❹对2.25题的条件作以下修改,对顺序表重新编写求得表C的算法。
(1)假设在同一表(A或B)中可能存在值相同的元素,但要求新生成的表C中的元素值各不相同;
(2)利用A表空间存放表C。
单链表
2.28❹对2.25题的条件作以下两点修改,对单链表重新编写求得表C的算法。
(1)假设在同一表(A或B)中可能存在值相同的元素,但要求新生成的表C中的元素值各不相同。
(2)利用原表(A表或B表)中的结点构造表C,并释放A表中的无用结点空间。
顺序表
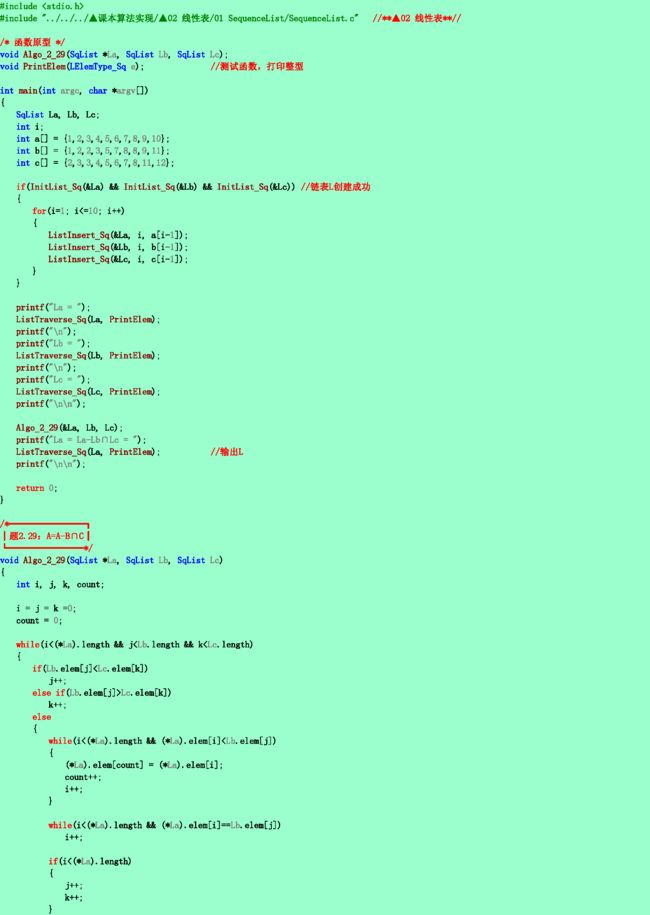
2.29❺ 已知A,B和C为三个递增有序的线性表,现要求对A表作如下操作:删去那些既在B表中出现,又在C表中出现的元素。试对顺序表编写实现上述操作的算法,并分析你的算法的时间复杂度(注意:同一表中各元素值可能相同)。
单链表
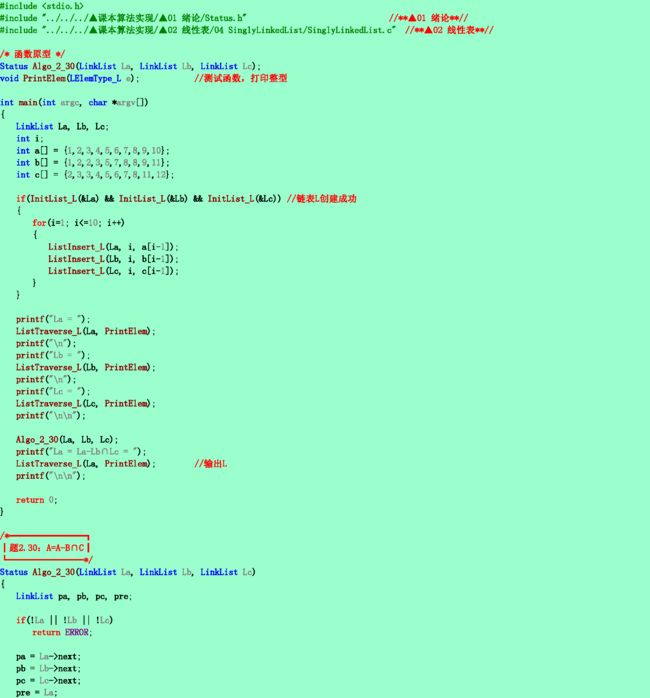
2.30❺ 要求同2.29题。试对单链表编写算法,请释放A表中的无用结点空间。
单循环链表
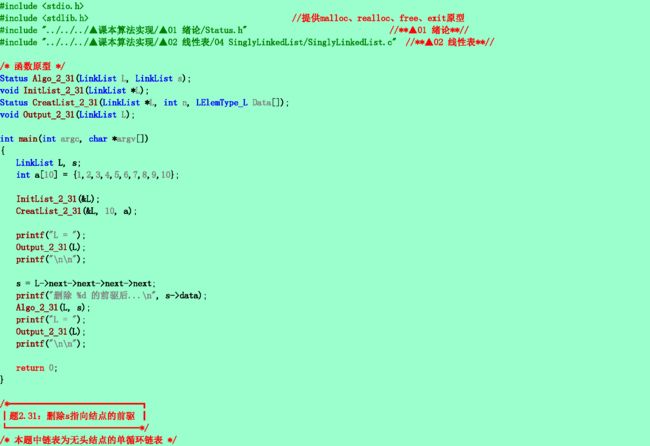
2.31❷ 假设某个单向循环链表的长度大于1,且表中既无头结点也无头指针。已知s为指向链表中某个结点的指针,试编写算法在链表中删除指针s所指结点的前驱结点。
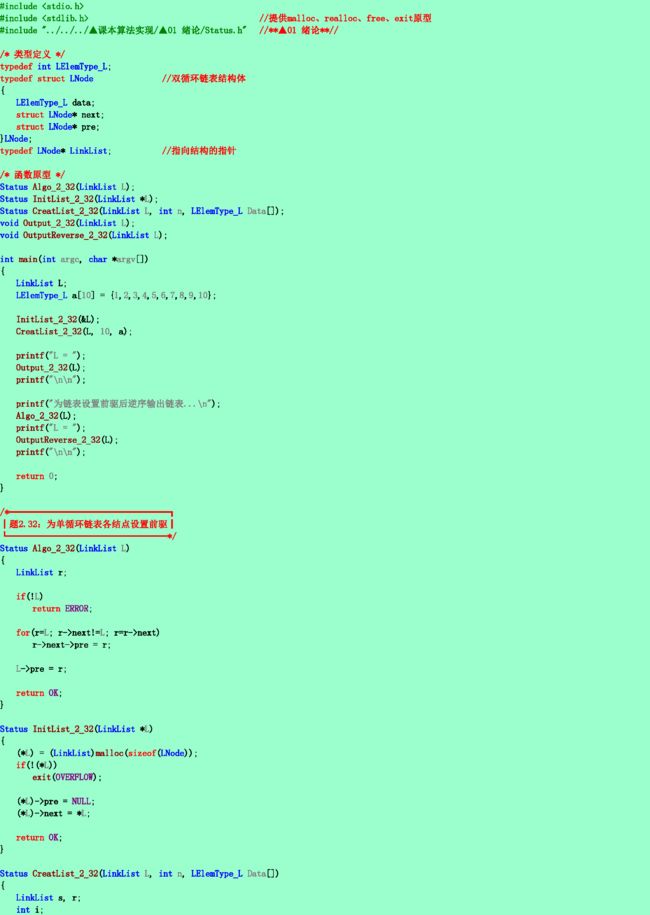
2.32❷ 已知有一个单向循环链表,其每个结点中含三个域:pre,data和next,其中data为数据域,next为指向后继结点的指针域,pre也为指针域,但它的值为空(NULL),试编写算法将此单向循环链表改为双向循环链表,即使pre称为指向前驱结点的指针域。
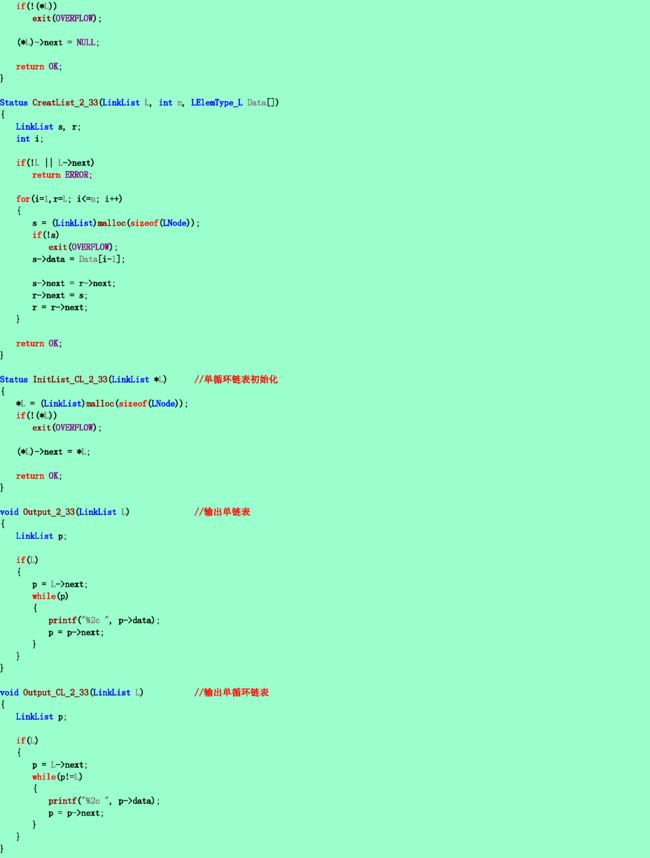
2.33❸ 已知由一个线性链表表示的线性表中含有三类字符的数据元素(如:字母字符、数字字符和其他字符),试编写算法将该线性链表分割为三个循环链表,其中每个循环链表表示的线性表中均只含一类字符。
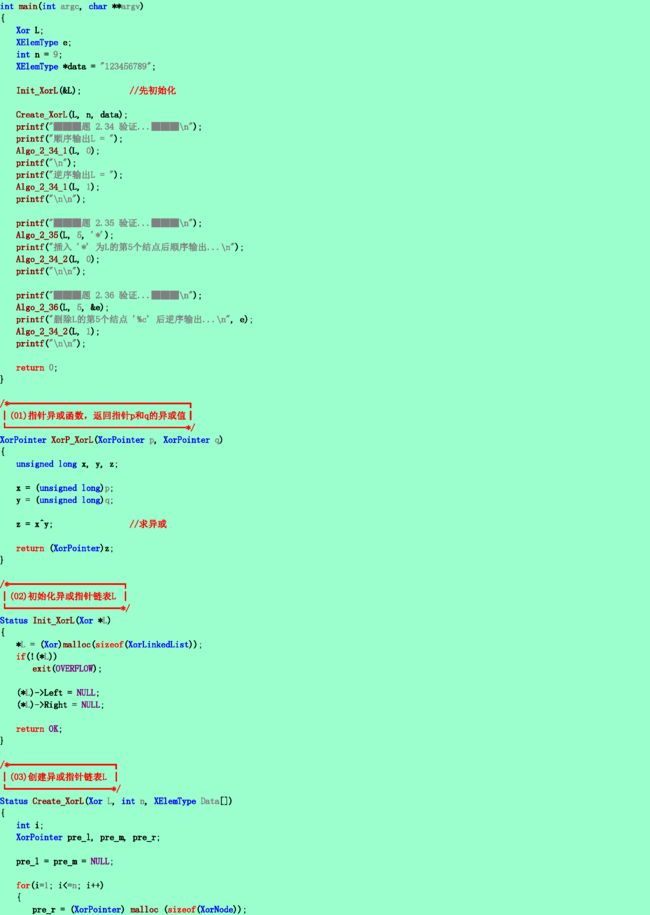
| typedef struct XorNode { char data; struct XorNode LRPtr; }XorNode, *XorPointer; typedef struct { //无头结点的异或指针双向链表 XorPointer Left, Right; //分别指向链表的左端和右端 }XorLinkedList; XorPointer XorP(XorPointer p, XorPointer q); //指针异或函数XorP返回指针p和q的异或(XOR)值 |
扩展的双链表(异或指针链表)
a⊕(a⊕b)=(a⊕a)⊕b=b
(a⊕b)⊕b=a⊕(b⊕b)=a
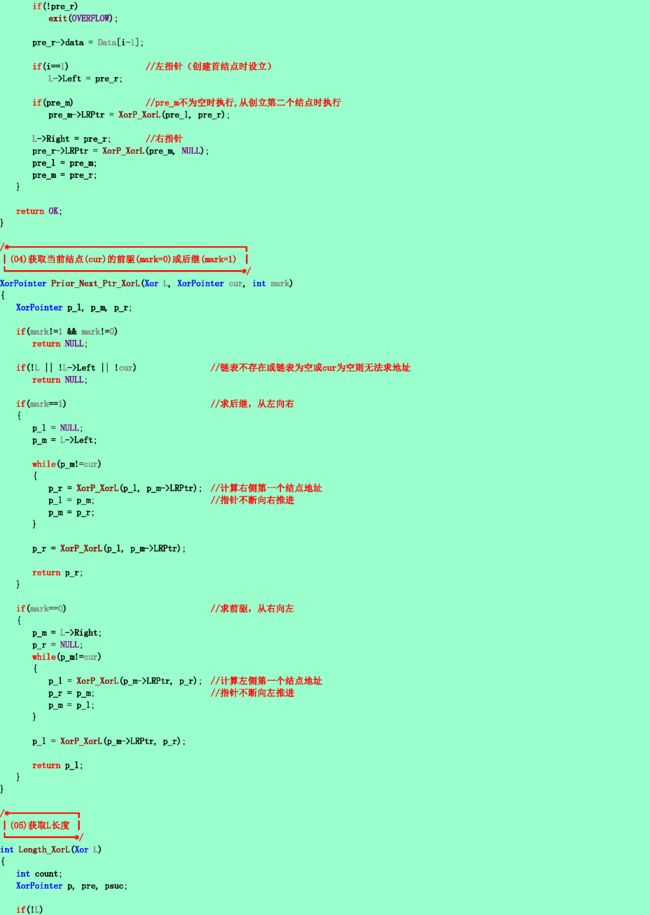
则可利用一个指针域来实现双向链表L。链表L中的每个结点只含两个域:data域和LRPtr域,其中LRPtr域存放该结点的左邻与右邻结点指针(不存在时为NULL)的异或。若设指针L.Left指向链表中的最左结点,L.Right指向链表中的最右结点,则可实现从左向右或从右向左遍历此双向链表的操作。试写一算法按任一方向依次输出链表中各元素的值。
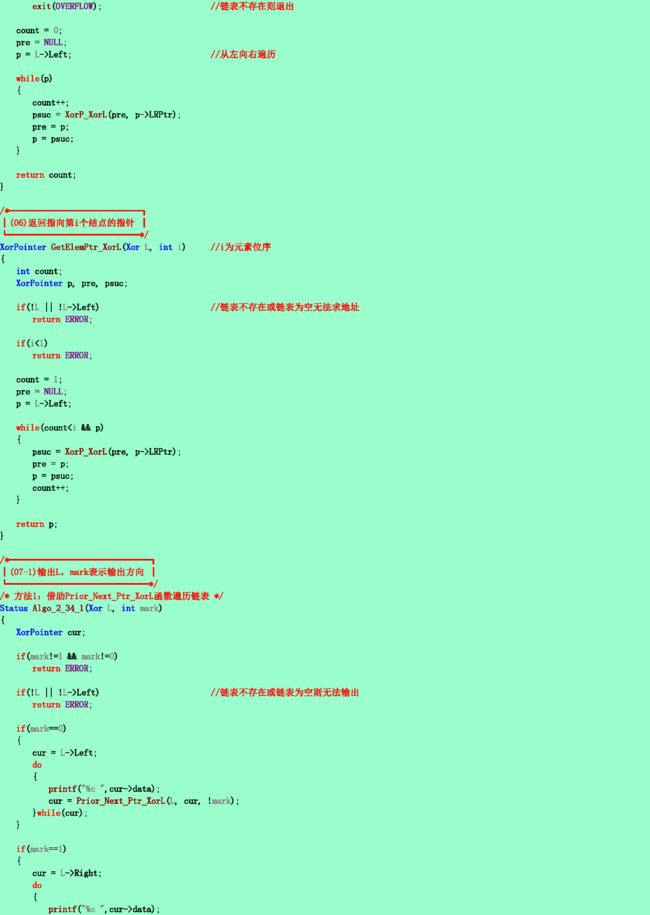
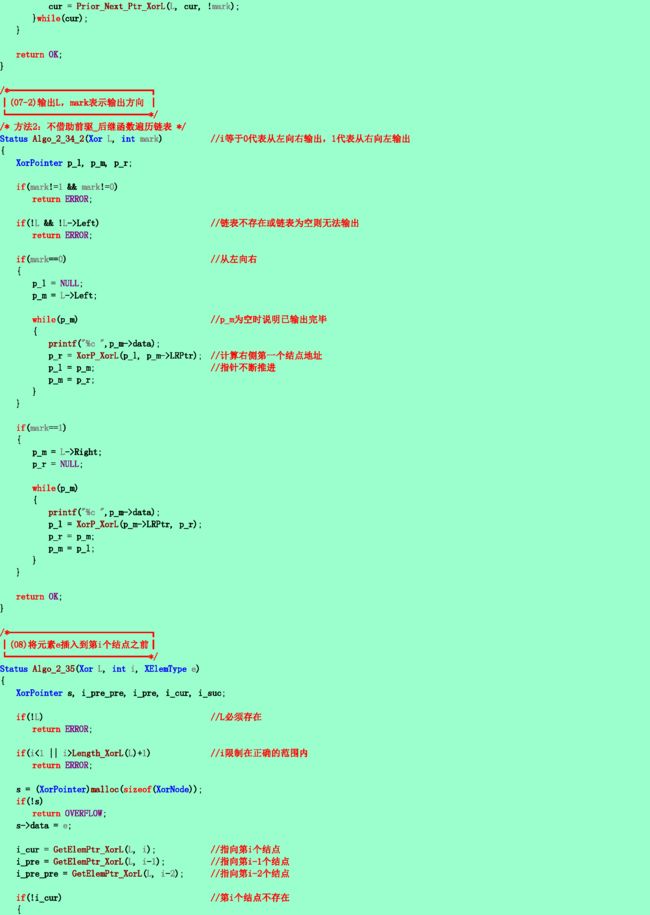
2.35❹ 采用2.34题所述的存储结构,写出在第i个结点之前插入一个结点的算法。
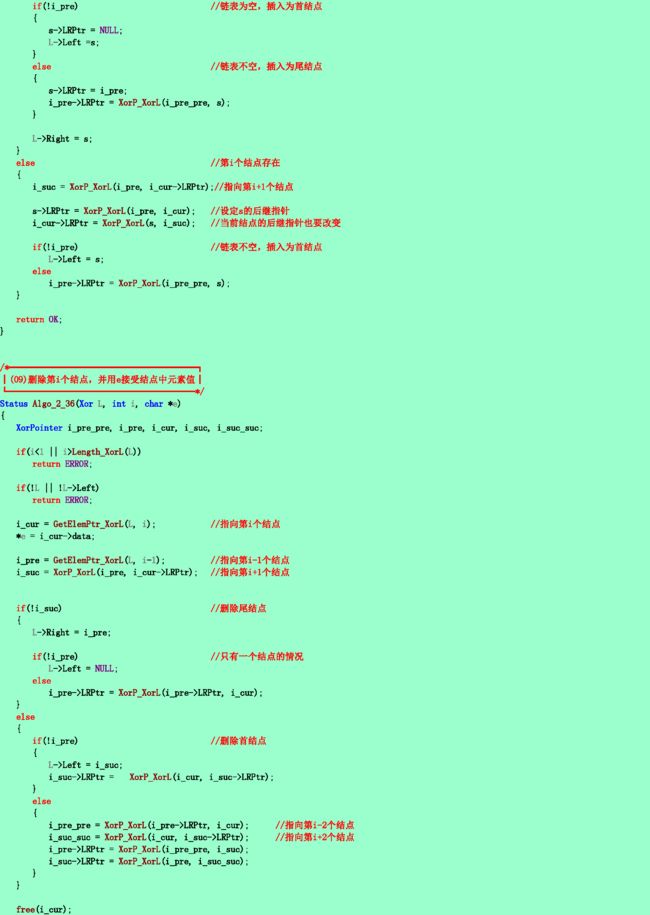
2.36❹ 采用2.34题所述的存储结构,写出删除第i个结点的算法。
双循环链表
2.37❹设以带头结点的双向循环链表表示的线性表L=(a1, a2, ..., an),试写一时间复杂度为O(n)的算法,将L改造为L=(a1, a3, ..., an, ..., a4, a2)。
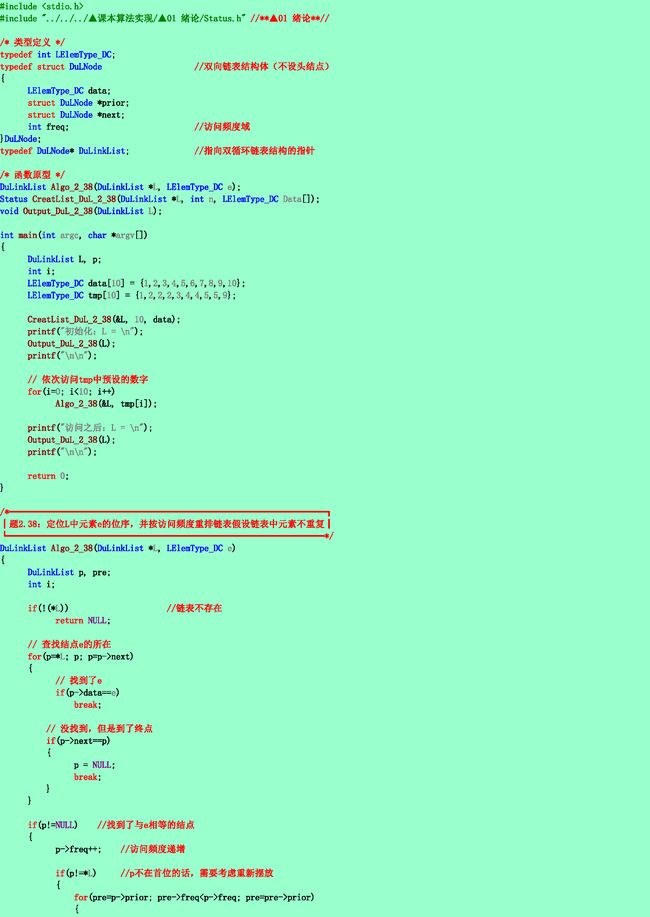
2.38❹设有一个双向循环链表,每个结点中除有pre,data和next三个域外,还增设了一个访问频度域freq。在链表被起用之前,频度域freq的值均初始化为零,而每当对链表进行一次LOCATE(L, x)的操作后,被访问的结点(即元素值等于x的结点)中的频度域freq的值便增1,同时调整链表中结点之间的次序,使其按访问频度非递增的次序顺序排列,以便始终保持被频繁访问的结点总是靠近表头结点,试编写符合上述要求的LOCATE操作的算法。
| typedef struct { int coef; int exp; }PolyTerm; typedef struct { //多项式的顺序存储结构 PolyTerm *data; int last; }SqPoly; |
多项式
2.39❸已知稀疏多项式![]() ,其中n=em>em-1>…>e1≥0,ci≠0(i=1,2,...,m),m≥1。试采用存储量同多项式项数m成正比的顺序存储结构,编写求Pn(x0)的算法(x0为给定值),并分析你的算法的时间复杂度。
,其中n=em>em-1>…>e1≥0,ci≠0(i=1,2,...,m),m≥1。试采用存储量同多项式项数m成正比的顺序存储结构,编写求Pn(x0)的算法(x0为给定值),并分析你的算法的时间复杂度。
![]()
2.40❸采用2.39题给定的条件和存储结构,编写求![]() 的算法,将结果多项式存放在新辟的空间中,并分析你的算法的时间复杂度。
的算法,将结果多项式存放在新辟的空间中,并分析你的算法的时间复杂度。
在2.41至2.42题中,稀疏多项式采用的循环链表存储结构LinkedPoly定义为:
| typedef struct PolyNode { PolyTerm data; struct PolyNode *next; }PolyNode, *PolyLink; typedef PolyLink LinkedPoly; |
2.41❷试以循环链表作稀疏多项式的存储结构,编写求其导函数的算法,要求利用原多项式中的结点空间存放其导函数(多项式),同时释放所有无用(被删)结点。
2.42❷试编写算法,将一个用循环链表表示的稀疏多项式分解成两个多项式,使这两个多项式中各自仅含奇次项或偶次项,并要求利用原链表中的结点空间构成这两个链表。