模拟退火 python
TSP +模拟退火
hello hello 依旧是一只努力进化的小白
效果图:

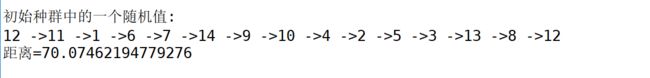

#!/usr/bin/python3
import sys
import math
import random
import matplotlib.pyplot as plt
import pylab as pl
import numpy as np
import sympy # 引入解方程的专业模块sympy
def Distance(X, n ):#计算两两城市之间的距离
D=np.zeros((n,n))
for i in range(0,n):
for j in range(i+1,n):
D[i][j] = math.sqrt((X[i][0] - X[j][0])**2 + (X[i][1] - X[j][1])**2);
D[j][i] = D[i][j];
return D
def useful(Route, citys):#路线 城市坐标
pl.mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
pl.mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
x = range(10) # 横轴的数据
y = [i*i for i in x] # 纵轴的数据
y1 = [i*i+10 for i in x] # 纵轴的数据
y2=[i*i+20 for i in x] #纵坐标
pl.title('title zyr')
pl.plot(x, y, '1m:', label=u'compare') # 加上label参数添加图例
pl.plot(x, y1, '>r--', label=u'set other') # 加上label参数添加图例
#标记遍历的 顺序
pl.plot(x,y2,'h',label=u'others')
pl.xlabel(u"横轴的数据")
pl.ylabel(u"纵轴的数据")
pl.legend() # 让图例生效
pl.show() # 显示绘制出的图
return
def DrawPath(Route, citys,n):#将路径用图的形式呈现出来欸
pl.rcParams['savefig.dpi'] =300 #图片像素
pl.rcParams['figure.dpi'] = 300 #分辨率
pl.mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
pl.mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
pl.title('初始化路线')
plt.xlim(xmax=25.5000,xmin=14.0000)#坐标上下界
plt.ylim(ymax=98.5000,ymin=91.5000)
x = [citys[Route[i%n]][0] for i in range(n+1)] # 横轴的数据
y = [citys[Route[i%n]][1] for i in range(n+1)] # 纵轴的数据
pl.plot(x, y, 'o--', label=u'初始化路线') # 加上label参数添加图例
#标记起点终点
pl.plot(citys[Route[0]][0], citys[Route[0]][1],'or' ,label=u'起点');
pl.plot(citys[Route[n-1]][0], citys[Route[n-1]][1],'og', label=u' 终点');
for i in range(n):
pl.text(citys[Route[i]][0],citys[Route[i]][1],i+1,color='k')#显示遍历顺序
pl.xlabel(u"X轴")
pl.ylabel(u"Y轴")
pl.legend() # 让图例生效
#pl.axis('off')
#pl.savefig('路径', dpi=300) #指定分辨
pl.show() # 显示绘制出的图
return
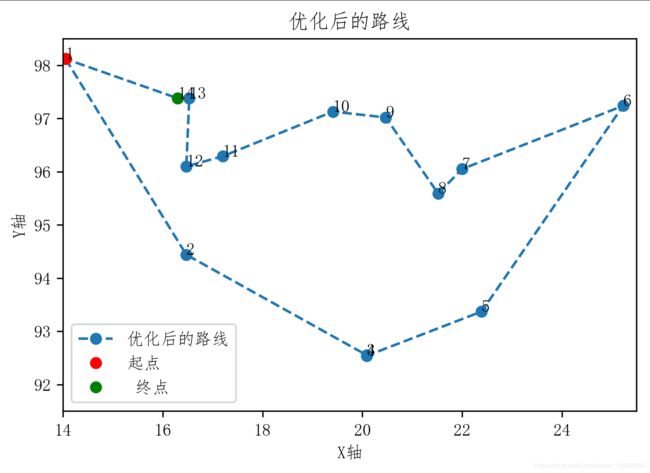
def DrawPath2(Route, citys,n):#将路径用图的形式呈现出来欸
pl.rcParams['savefig.dpi'] =300 #图片像素
pl.rcParams['figure.dpi'] = 300 #分辨率
pl.mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
pl.mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
pl.title('优化后的路线')
plt.xlim(xmax=25.5000,xmin=14.0000)#坐标上下界
plt.ylim(ymax=98.5000,ymin=91.5000)
x = [citys[Route[i%n]][0] for i in range(n+1)] # 横轴的数据
y = [citys[Route[i%n]][1] for i in range(n+1)] # 纵轴的数据
pl.plot(x, y, 'o--', label=u'优化后的路线') # 加上label参数添加图例
#标记起点终点
pl.plot(citys[Route[0]][0], citys[Route[0]][1],'or' ,label=u'起点');
pl.plot(citys[Route[n-1]][0], citys[Route[n-1]][1],'og', label=u' 终点');
for i in range(n):
pl.text(citys[Route[i]][0],citys[Route[i]][1],i+1,color='k')#显示遍历顺序
pl.xlabel(u"X轴")
pl.ylabel(u"Y轴")
pl.legend() # 让图例生效
#pl.axis('off')
#pl.savefig('路径', dpi=300) #指定分辨
pl.show() # 显示绘制出的图
return
def PathLength(D, Route,n):#计算路径长度
length=0.0
for i in range(0,n):
length+=D[Route[i]][Route[(i+1)%n]]
return length
def NewAnswer(S1,n):#随机产生 新的解
S2=S1.copy()
random.seed();
a=random.randint(0,n-1)
random.seed();
b=random.randint(0,n-1)
w=S1[a]
S2[a]=S1[b]
S2[b]=w
#print(a,b)
return S2
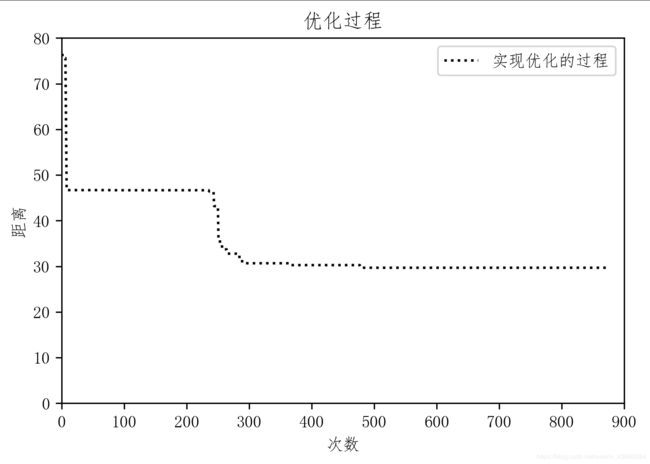
def process(count,Height):
pl.rcParams['savefig.dpi'] =300 #图片像素
pl.rcParams['figure.dpi'] = 300 #分辨率
pl.mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
pl.mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
pl.title('优化过程')
plt.xlim(xmax=900,xmin=0)#坐标上下界
plt.ylim(ymax=80,ymin=0)
x = range(1,count+1) # 横轴的数据
y = [Height[i] for i in range(1,count+1)] # 纵轴的数据
pl.plot(x, y, ':k', label=u'实现优化的过程') # 加上label参数添加图例
#标记起点终点
pl.xlabel(u"次数")
pl.ylabel(u"距离")
pl.legend() # 让图例生效
#pl.axis('off')
#pl.savefig('路径', dpi=300) #指定分辨
pl.show() # 显示绘制出的图
return
def Metropolis(S1, S2, D, T,n):
# 输入
# S1: 当前解
# S2: 新解
# D: 距离矩阵(两两城市的之间的距离)
# T: 当前温度
# 输出
# S: 下一个当前解
# R: 下一个当前解的路线距离
R1 = PathLength(D,S1,n); #计算S1路线长度
R2 = PathLength(D,S2,n); # 计算S2路线长度
dC = R2 - R1; # 计算能力之差
#print(S1,S2)
#print(R2,R1,dC)
if (dC < 0.0): #如果能力降低 接受新路线
S = S2; #接受新解
R = R2;
elif(math.exp(float(-dC)/float(T))>= (random.random())): #以exp(-dC/T)概率接受新路线 这的rand 返回(0,1)之间的随机数
S = S2;
R = R2;
#print(float(-dC)/float(T))
else: # 不接受新路线
S = S1;
R = R1;
return S,R;
X =np.array([ [16.4700 , 96.1000],
[ 16.4700 , 94.4400],
[20.0900 , 92.5400],
[22.3900 , 93.3700],
[25.2300 , 97.2400],
[22.0000 , 96.0500],
[20.4700 , 97.0200],
[17.2000 , 96.2900],
[16.3000 , 97.3800],
[14.0500 , 98.1200],
[16.5300 , 97.3800],
[21.5200 , 95.5900],
[19.4100 , 97.1300],
[20.0900 , 92.5500]]);#每个城市点的x,y坐标
n=(X.shape[0])#这个矩阵有几行 啊
#print(n)
D=Distance(X,n)#算出距离矩阵
#print(D)
T0 = 1e10; #初始温度
Tf = 1e-30; #终止温度
#print(T0,Tf)
q=0.90
# 计算迭代的次数 T0 * (0.9)^x = Tf
Time =1000
#print(Time)
count = 0; # 初始化迭代计数
Obj = np.zeros((Time, 1)); # 目标值矩阵初始化
path = np.zeros((Time, n),dtype=int); # 每代的最优路线矩阵初始化
#随机初始化一个路线
S1=np.random.permutation(n);
#print(S1)
DrawPath(S1, X,n) ;#随机生成一个初始路径
print("初始种群中的一个随机值:")
for i in range(n):
print(S1[i]+1,"->",end="")
print(S1[0]+1)
print("距离=",end="")
rlength = PathLength(D, S1,n);
print(rlength)
while T0>=Tf:
count =count +1#更新迭代次数
S2=NewAnswer(S1,n)#随机产生一个新的解
S1,R= Metropolis(S1, S2, D,T0,n)
if ((count == 1) or( R < Obj[count-1])): #选
Obj[count] = R
else:#不选
Obj[count] = Obj[count-1]
path[count] = S1 # 记录每次迭代的路线
T0=T0*1.0*q #以q的速率降温
#改进的过程
process(count,Obj)
#最优解
DrawPath2(path[count],X,n)
print("最优解")
for i in range(n):
print(path[count][i]+1,"->",end="")
print(path[count][0]+1)
print("距离=",end="")
print(Obj[count])