CORDIC算法基本原理
引言
某些复杂的计算,例如三角函数和除法运算等涉及到大量浮点运算的计算任务,是数字电路天生的瓶颈所在。在某些场景下,可以使用查找表方法或者采用级数展开的方法来实现三角函数等运算功能。但是,这两种方法可能会占用大量的存储资源和硬件乘法计算单元,而想要节省资源,就要以牺牲精度为代价。
相对于前两种方法,CORDIC算法具有很大优势。首先,在计算过程中,它不使用任何的硬件乘法器单元,所涉及的只有移位和累加。然后,对于存储资源的占用,它仅仅需要少量的数据需要预先存储。在实际的数字电路设计中,可以将其设计为流水线方式或者是迭代复用方式,以提高运算速度或者是减少资源占用。
一、矢量旋转公式
CORDIC算法最最基本理论基础,是矢量旋转公式。即矢量 A ( x , y ) A\left( {x,y} \right) A(x,y)顺时针旋转 θ \theta θ之后,得到的矢量 ( x ′ , y ′ ) \left( {x',y'} \right) (x′,y′)可以表示为 (式1):
x ′ = x cos θ + y sin θ , y ′ = y cos θ − x sin θ . \begin{array}{l} x' = x\cos \theta + y\sin \theta ,\\ y' = y\cos \theta - x\sin \theta . \end{array} x′=xcosθ+ysinθ,y′=ycosθ−xsinθ.
下面用一张图来表示上述公式的原理。
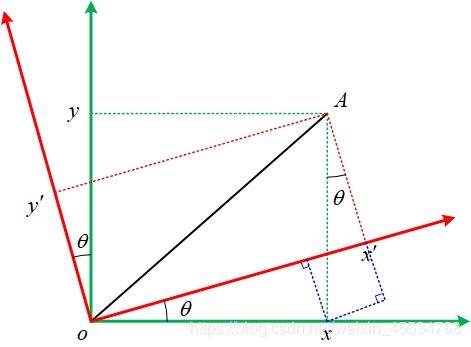
如上图所示,矢量 A ( x , y ) A\left( {x,y} \right) A(x,y)顺时针旋转 θ \theta θ,等效为矢量坐标系逆时针旋转 θ \theta θ。矢量 A A A在旋转后的新的坐标系上的映射,就是我们所要求的 ( x ′ , y ′ ) \left( {x',y'} \right) (x′,y′)。图中蓝色虚线为辅助线,在辅助线的帮助下,上述公式的原理不言自明。
二、矢量旋转公式的变换
考虑一种情景:矢量 A A A不断地逆时针旋转,直至旋转到与横坐标平行。如下图所示:

可得 (式2),
x n + 1 = x n cos θ n − y n sin θ n = cos θ n ( x n − y tan θ n ) y n + 1 = y n cos θ n + x n sin θ n = cos θ n ( y n + x n tan θ n ) \begin{array}{l} x_{n + 1}= x_n\cos \theta_n - y_n\sin \theta_n = \cos \theta_n \left( {x_n - y\tan \theta_n } \right)\\ y_{n + 1} = y_n\cos \theta_n + x_n\sin \theta_n = \cos \theta_n \left( {y_n + x_n\tan \theta_n } \right) \end{array} xn+1=xncosθn−ynsinθn=cosθn(xn−ytanθn)yn+1=yncosθn+xnsinθn=cosθn(yn+xntanθn)
每旋转一次,上述公式就迭代一次。CORDIC算法的核心就是矢量不断旋转,上述公式多次进行迭代的过程。 可见,此时的迭代运算,需要三角函数和乘法的计算,十分复杂,因此需要对其进行简化。
首先,如果把每次迭代过程中的 cos θ n \cos \theta_n cosθn忽略 (式3),相当于在向量旋转过程中,对矢量进行了缩放,缩放因子为 1 cos θ n \frac{1}{{\cos {\theta _n}}} cosθn1。
x n + 1 = x n − y tan θ n y n + 1 = y n + x n tan θ n \begin{array}{l} x_{n + 1}= {x_n - y\tan \theta_n } \\ y_{n + 1} = {y_n + x_n\tan \theta_n } \end{array} xn+1=xn−ytanθnyn+1=yn+xntanθn
此时,迭代过程减少了一部分三角函数运算和乘法运算,但是还不够。
在每次旋转中,限定 θ n \theta_n θn取某些特殊的值,使得 (式4):
tan θ 0 = 2 0 , tan θ 1 = 2 − 1 , tan θ 2 = 2 − 2 , ⋯ tan θ n = 2 − n , ⋯ \begin{array}{l} \tan {\theta _0} = {2^0},\\ \tan {\theta _1} = {2^{ - 1}},\\ \tan {\theta _2} = {2^{ - 2}},\\ \cdots \\ \tan {\theta _n} = {2^{ - n}},\\ \cdots \end{array} tanθ0=20,tanθ1=2−1,tanθ2=2−2,⋯tanθn=2−n,⋯
那么可以将迭代公式变成下面迭代公式所示 (式5) :
x n + 1 = x n − d n ( y n ⋅ 2 − n ) y n + 1 = y n + d n ( x n ⋅ 2 − n ) \begin{array}{l} {x_{n + 1}} = {x_n} - {d_n}\left( {y_n \cdot {2^{ - n}}} \right)\\ {y_{n + 1}} = {y_n} + {d_n}\left( {x_n \cdot {2^{ - n}}} \right) \end{array} xn+1=xn−dn(yn⋅2−n)yn+1=yn+dn(xn⋅2−n)
可见,在每次迭代过程中,选定某些特殊的旋转角,使用移位运算来代替乘法运算。为了使得矢量可以不断接近目标位置,旋转的角度随着旋转次数的增加而减少的。同时,旋转方向是不断调整的,即如果越过了目标位置,则下一次旋转方向要取反。我们约定,逆时针方向时, d n = 1 {d_n =1} dn=1。
通过上述一系列的变换,CORDIC算法所使用的迭代过程,对于硬件实现来说就十分友好了。
三、COEDIC算法的实际应用
下面,我们使用COEDIC算法来求解具体的计算问题。
- 正弦函数 sin ( z ) \sin \left( z \right) sin(z)和余弦函数 cos ( z ) \cos \left( z \right) cos(z)的求解
可知 (式6),
x n + 1 = x n − d n ( y n ⋅ tan θ n ) = 1 cos θ n [ cos θ n x n − d n ( y n ⋅ sin θ n ) ] y n + 1 = y n + d n ( x n ⋅ tan θ n ) = 1 cos θ n [ cos θ n y n + d n ( x n ⋅ sin θ n ) ] \begin{array}{l} {x_{n + 1}} = {x_n} - {d_n}\left( {y_n \cdot \tan {\theta _n}} \right) = \frac{1}{{\cos {\theta_n}}}\left[ {\cos {\theta _n}{x_n} - {d_n}\left( {y_n \cdot \sin {\theta _n}} \right)} \right]\\ {y_{n + 1}} = {y_n} + {d_n}\left( {x_n \cdot \tan {\theta _n}} \right) = \frac{1}{{\cos {\theta _n}}}\left[ {\cos {\theta _n}{y_n} + {d_n}\left( {x_n \cdot \sin {\theta _n}} \right)} \right] \end{array} xn+1=xn−dn(yn⋅tanθn)=cosθn1[cosθnxn−dn(yn⋅sinθn)]yn+1=yn+dn(xn⋅tanθn)=cosθn1[cosθnyn+dn(xn⋅sinθn)]
因此有 (式7):
x n + 1 = Π n 1 cos θ i [ cos ( ∑ i = 0 n d i θ i ) x 0 − sin ( ∑ i = 0 n d i θ i ) y 0 ] y n + 1 = Π n 1 cos θ i [ cos ( ∑ i = 0 n d i θ i ) y 0 + sin ( ∑ i = 0 n d i θ i ) x 0 ] \begin{array}{l} {x_{n + 1}} = \mathop \Pi \limits_{n } \frac{1}{{\cos {\theta _i}}}\left[ {\cos \left( {\sum\limits_{i = 0}^{n } {{d_i}{\theta _i}} } \right){x_0} - \sin \left( {\sum\limits_{i= 0}^{n} {{d_i}{\theta _i}} } \right){y_0}} \right]\\ {y_{n + 1}} = \mathop \Pi \limits_{n} \frac{1}{{\cos {\theta _i}}}\left[ {\cos \left( {\sum\limits_{i = 0}^{n } {{d_i}{\theta _i}} } \right){y_0} + \sin \left( {\sum\limits_{i = 0}^{n} {{d_i}{\theta _i}} } \right){x_0}} \right] \end{array} xn+1=nΠcosθi1[cos(i=0∑ndiθi)x0−sin(i=0∑ndiθi)y0]yn+1=nΠcosθi1[cos(i=0∑ndiθi)y0+sin(i=0∑ndiθi)x0]
为了简单,令 k n = Π n 1 cos θ i {k_{n }} = \mathop \Pi \limits_{n} \frac{1}{{\cos {\theta _i}}} kn=nΠcosθi1。
设置迭代初始值 x 0 = 1 k n {x_0} = \frac{1}{{{k_{n}}}} x0=kn1, y n = 0 y_n = 0 yn=0。每次迭代的角度旋转方向取 d n = s i g n ( z − ∑ i = 0 n − 1 d i θ i ) {d_{n}} = sign\left( {z - \sum\limits_{i = 0}^{n-1} {{d_i}\theta {}_i} } \right) dn=sign(z−i=0∑n−1diθi),可知,随着迭代的深入,旋转的角度 ∑ i = 0 n d i θ i \sum\limits_{i = 0}^n {{d_i}\theta {}_i} i=0∑ndiθi 会逐渐的趋近于 z z z。当迭代到第 ( n + 1 ) \left(n+1\right) (n+1)次时,上述公式可化为 (式8):
x n + 1 = k n [ cos ( ∑ i = 0 n d i θ i ) x 0 − sin ( ∑ i = 0 n d i θ i ) y 0 ] = cos ( ∑ i = 0 n d i θ i ) ⇒ cos z y n + 1 = k n [ cos ( ∑ i = 0 n d i θ i ) y 0 + sin ( ∑ i = 0 n d i θ i ) x 0 ] = sin ( ∑ i = 0 n d i θ i ) ⇒ sin z \begin{array}{l} {x_{n + 1}} = {k_n}\left[ {\cos \left( {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } \right){x_0} - \sin \left( {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } \right){y_0}} \right] = \cos \left( {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } \right) \Rightarrow \cos z\\ {y_{n{\rm{ + 1}}}} = {k_n}\left[ {\cos \left( {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } \right){y_0} + \sin \left( {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } \right){x_0}} \right] = \sin \left( {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } \right) \Rightarrow \sin z \end{array} xn+1=kn[cos(i=0∑ndiθi)x0−sin(i=0∑ndiθi)y0]=cos(i=0∑ndiθi)⇒coszyn+1=kn[cos(i=0∑ndiθi)y0+sin(i=0∑ndiθi)x0]=sin(i=0∑ndiθi)⇒sinz
在这种初始值预设和旋转方向下,不断进行(式6)的计算,也就是(式5)的计算,最终计算出 cos z \cos z cosz和 sin z \sin z sinz的近似值。迭代次数 n n n越大,近似的精度越高。 - 反正切函数 arctan ( y / x ) \arctan (y/x) arctan(y/x)的求解
对于反正切函数来说,参照正弦余弦的模式,只需要初始值 ( x 0 , y 0 ) \left( {{x_0},{y_0}} \right) (x0,y0) 设置为要求的正切参数的 ( x , y ) \left( {x,y} \right) (x,y),将迭代方向取为 d n = − s i g n ( x n y n ) {d_n} = - sign\left( {{x_n}{y_n}} \right) dn=−sign(xnyn),即不断朝着使得 y n = 0 {y_n} = 0 yn=0的方向进行旋转,因此,最终 ∑ i = 0 n d i θ i {\sum\limits_{i = 0}^n {{d_i}{\theta _i}} } i=0∑ndiθi所累积的角度,即为所求的反正切角度。 - 除法运算
除法运算,因为不涉及到三角函数,只需要按照CORDIC算法的思想去求即可。除法运算的CODRDIC算法的迭代公式为:
x n + 1 = x 0 y n + 1 = y n − d n 2 − n ⋅ x n \begin{array}{l} {x_{n + 1}} = {x_0}\\ {y_{n + 1}} = {y_n} - {d_n}{2^{ - n}} \cdot {x_n} \end{array} xn+1=x0yn+1=yn−dn2−n⋅xn
迭代方向 d n = s i g n ( y n − 1 ) {d_n} = sign\left( {{y_{n - 1}}} \right) dn=sign(yn−1),即不断地朝着 y n + 1 = 0 {y_{n + 1}} = 0 yn+1=0 的方向去迭代。
这个是有问题的吧?如果 x 0 ≪ y 0 {x_0} \ll {y_0} x0≪y0,由于 ∑ n = 0 ∞ 2 − n = 2 \sum\limits_{n = 0}^\infty {{2^{ - n}}} = 2 n=0∑∞2−n=2,上述迭代永远也不会收敛,差距太大了。
能否解决上述问题?个人认为,可以对n的值做预设,不能从0开始,需要根据 x 0 x_0 x0 和 y 0 y_0 y0来决定n的初始值。根据 ∑ n = i ∞ 2 − n = 2 1 − i \sum\limits_{n = i}^\infty {{2^{ - n}}} = {2^{1 - i}} n=i∑∞2−n=21−i,可以根据 x 0 x_0 x0 和 y 0 y_0 y0实际有效位数的差异,来决定,例如 y 0 y_0 y0 的有效位宽是5, x 0 x_0 x0 的有效位宽是2,因此他们的商可能在8左右,此时n的初始值,应该取-2开始。
================================================
参考资料:《通信IC设计》