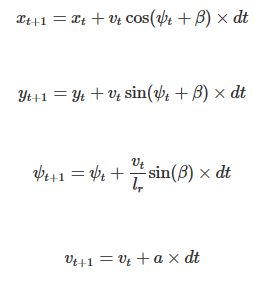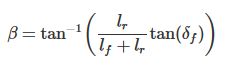运动学自行车模型和动力学自行车模型
作者简介:申泽邦(Adam Shan),兰州大学在读硕士研究生,主攻无人驾驶,深度学习;文章来源:https://blog.csdn.net/adamshan/article/details/78696874
在了解高级的车辆控制算法之前,掌握车辆运动模型是非常有必要的。车辆运动模型就是一类能够描述我们的车辆的运动规律的模型。显然,越复杂的模型就越接近现实中的车辆运动规律,本节我们一起了解一下两个广泛使用的车辆模型——运动学自行车模型(Kinematic Bicycle Model) 和 动力学自行车模型(Dynamic Bicycle Model)
无人驾驶系统往往分成感知,决策和控制三个模块,其中无人车的路径规划和底层控制是工作在不同的层的,路径规划层往往会基于更加高层的(感知层,定位层)的信息和底层的(控制层)的实时信息指定行驶的路径,那么从路径规划层传来的就是车辆的参考路径,控制系统需要做的就是严格按照这个参考路径(以及速度等控制输入量)去驾驶我们的车辆,一般来说,我们会用多项式的行驶来描述这个路径曲线,如下所示的三次多项式就可以描述绝大多数的路径了:
y = a x 3 + b x 2 + c x + d y=ax^3+bx^2+cx+d y=ax3+bx2+cx+d
无人车的控制依赖于一项称为 模型预测控制(Model Predictive Control) 的简单技术,这种控制的方法是产生一系列的可行的(也就是说在实际上车辆能够做到的)控制输入,基于一定的算法(往往是带约束的非线性优化算法)来调整这一系列的控制输入,使得一个 损失函数(cost function) 最小化,这个损失函数的求解就要依赖于车辆的运动学或者动力学模型的输出和参考的路径的差值求得,这些模型正是本节介绍的内容。
自行车模型(Bicycle Model)
首先我们要简化汽车运动,其中自行车模型就是简单且有效的简化方式。自行车模型基于如下几个假设:
-
车辆在垂直方向的运动被忽略掉了,也就是说我们描述的车辆是一个二维平面上的运动物体(可以等价与我们是站在天空中的俯视视角)
-
我们假设车辆的结构就像自行车一样,也就是说车辆的前面两个轮胎拥有一直的角度和转速等,同样后面的两个轮胎也是如此,那么前后的轮胎就可以各用一个轮胎来描述
-
我们假设车辆运动也和自行车一样,这意味着是前面的轮胎控制这车辆的转角
首先我们简单的在一个二维平面上描述一个车辆:
![]()
其中 θ是其在Yaw方向的偏转角度,它是相对于x轴的逆时针方向的角度,v是θ方向的速度,L是车辆的轴距(前后轮胎的距离), (x,y)是车辆的坐标。
下图是该车辆的自行车模型:
![]()
运动学自行车模型
作为一种自行车模型,运动学自行车模型也假定车辆形如一辆自行车,整个的控制量可以简化为 ( a , δ f ) (a, δ_{f}) (a,δf),其中a是车辆的加速度,踩油门踏板意味着正的加速度,踩刹车踏板意味着负的加速度。 δ f ) δ_{f}) δf)是我们的方向盘转角,我们假定这个方向盘转角就是前轮胎当前的转角。这样,我们使用两个量描述了车辆的控制输入(control input)。
然后我们定义我们模型中的状态量,运动学自行车模型使用四个状态量来描述车辆的当前状态:
x: 即车辆当前的坐标
y: 即车辆当前的坐标
ψ: 即车辆当前的偏航角(Yaw方向的偏角,往往用弧度来描述, 逆时针方向为正)
v: 即车辆的速度
一个简单的运动学自行车模型如图所示:
![]()
其中 l f l_{f} lf和 l r l_{r} lr为前轮和后轮到车辆重心的距离。那么更具运动学定理,运动学自行车模型中的各个状态量的更新公式如下:
由于绝大多数的汽车后轮都不能够偏转,所以我们的自行车模型就假定后轮的转角控制输入 δ r = 0 δ_{r}=0 δr=0,也就是说,方向盘上的控制输入,都反映到了前轮的转角上了。
动力学自行车模型
前面的车辆运动学自行车模型其实还隐含着一个重要的假设,那就是: 车前轮的方向即是车辆当前的速度方向,在实际车辆运动过程中,当车辆在以相对高的速度行驶时,车轮的方向并不一定车辆当前的速度方向,这个时候,我们引入车辆的动力学自行车模型。
车辆动力学模型通过对轮胎和路面之间的复杂相互作用来描述车辆的运动。在一个动力模型中,我们需要考虑各种各样的力的作用,他们可以大致分为两类: 纵向力(Longitudinal force) 和 侧向力(Lateral force), 纵向力就是使车辆前后移动的力量,而侧向力则促使车辆在横向移动,在力的相互作用过程中,轮胎起着决定性的作用(根据一定的物理常识,轮胎是车辆运动的一个重要的力的来源)。
我们仍然以上图为例,考虑一个简单的动力学模型,这个模型的各个状态量为 ( x ˙ , y ˙ , φ ˙ , X , Y ) (\dot{x},\dot{y},\dot{\varphi},X,Y) (x˙,y˙,φ˙,X,Y),其中 x ˙ \dot{x} x˙和 y ˙ \dot{y} y˙表示的是车身的纵向和侧向速度, φ ˙ \dot{\varphi} φ˙表示的是偏航角速度,(X,Y)表示车车身的当前坐标,这些状态量在时间尺度上的微分方程如下:
![]()
其中,m和 I z I_{z} Iz分别表示车辆的质量和偏航惯性(yaw inertia), F c , f F_{c,f} Fc,f和 F c , r F_{c,r} Fc,r分别表示的是前后轮胎受到的侧向力,他们可以通过具体的轮胎模型求得,在简单的线性轮胎模型中, F c , i , ( i = f o r r ) F_{c,i}, (i=f or r) Fc,i,(i=forr)表示为:
F c , i = C α i α i F_{c,i}=C_{\alpha_{i}}\alpha_{i} Fc,i=Cαiαi
其中 α i \alpha_{i} αi是轮胎的偏转角,这个偏转角是指轮胎当前的朝向和当前的速度的夹角, C α i C_{\alpha_{i}} Cαi被称为轮胎偏滚刚度(tire cornering stiffness)。
运动学自行车模型的Python实现
我们使用Python代码简单实现一个运动学自行车模型类,作为后期我们使用模型预测控制的车辆模型。
from __future__ import print_function
import math
class KinematicModel(object):
def __init__(self, x, y, psi, v, f_len, r_len):
self.x = x
self.y = y
self.psi = psi
self.v = v
self.f_len = f_len
self.r_len = r_len
def get_state(self):
return self.x, self.y, self.psi, self.v
def update_state(self, a, delta, dt):
beta = math.atan((self.r_len / (self.r_len + self.f_len)) * math.tan(delta))
self.x = self.x + self.v * math.cos(self.psi * beta) * dt
self.y = self.y + self.v * math.sin(self.psi * beta) * dt
self.psi = self.psi + (self.v / self.f_len) * math.sin(beta) * dt
self.v = self.v + a * dt
return self.x, self.y, self.psi, self.v
这个简易的车辆模型中,我们的控制量包含了一个前胎的转角和一个加速度a,由于受车辆机械的限制,车辆本身有很多动作是实现不了的,比如说加速度a的值不可能过大,轮胎的转角也会有极限,我们称这种性质叫做模型非完整性(model nonholonomic)