Simulink —— 三相交流控制系统中的坐标变换
参考资料:Simulink - Mathematical Transforms
在交流控制系统中:
当三相平衡时,电压和电流分别幅值相等,相位互差120°,为了方便进行数学推导及控制,提出了Clarke,Park变换以及逆变换。
而当三相不平衡时,电压和电流的信号会出现幅值不相等以及相位互差不为120°的情况,于是引出了正序,负序,零序的概念,任意三相交流信号均可由正序,负序,零序组成,提出了对称分量变换
列表如下:
| 三相平衡变换 | 说明 |
|---|---|
| Clarke Transform | abc to αβ0 |
| Inverse Clarke Transform | αβ0 to abc |
| Park Transform | abc to dq0 |
| Inverse Park Transform | dq0 to abc |
| Clarke to Park Angle Transform | αβ0 to dq0 |
| Park to Clarke Angle Transform | dq0 to αβ0 |
| 三相不平衡变换 | 说明 |
|---|---|
| Symmetrical-Components Transform | abc to ±0 |
| Inverse Symmetrical-Components Transform | ±0 to abc |
点击图片可查看高清版本
Clarke Transform
关于等幅变换和等功率变换中系数的确定可以参考博文:
https://blog.csdn.net/jaysur/article/details/100673823
Inverse Clarke Transform
clarke变换的作用主要是将互差120°的坐标系转换成互差90°的坐标系,这里是将abc的坐标系转换成αβ0,而0轴是与αβ垂直的,可理解为笛卡尔坐标系中的xyz轴,称为三相静止坐标系到两相静止坐标系的转换,在实际电机控制的工程中,往往会忽略0轴,仅用α和β来进行计算,同时考虑三相中a+b+c=0这个特性,化简后可以仅用ab来表示αβ,这样在采集电压电流时,仅用2个采样电路即可,节省成本。
另外,clarke分为两种转换方式,即等幅值变换和等功率变换,等幅值变换值的是变换前后,各分量的幅值相等,如仿真图中,变换前后波形的幅值均为100,比较直观,所以工程中通常采用这种方式。而等功率变换中的变换矩阵是正交矩阵,即逆等于其转置,这种通常在需要功率控制中使用。
两种方式仅是系数上的差别,甚至实际使用时连前面的系数都可以省略,并入PID的Kp中。
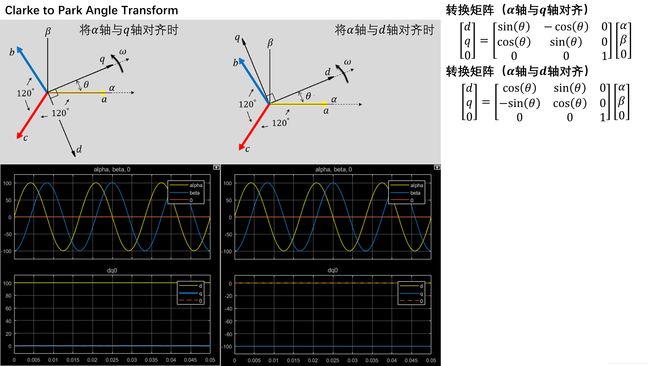
Clarke to Park Angle Transform
Park to Clarke Angle Transform
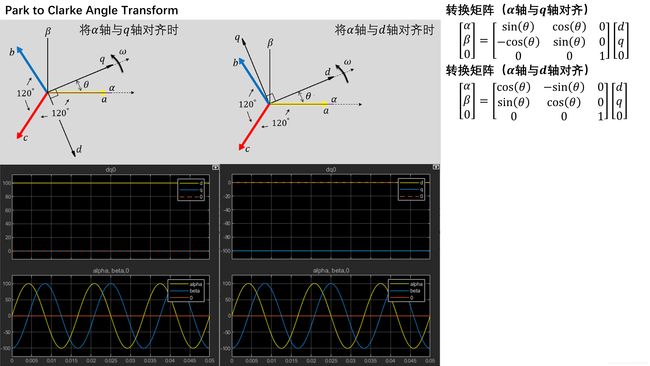
clarke与park之间的转换也是非常常用的变换,从变换形式来看,αβ的波形为互差90°的正弦,可以等效成sin和cos函数,波形的变化等效成一个向量的模和相角,而park变换就是将相角这个部分从向量里分离出来,仅剩下向量的模,这样对向量模长的控制,最终可以达到对abc三相的幅值控制,简化了一系列的相位计算,称为两相静止坐标系到两相旋转坐标系的转换。
park变换也具有两种形式,即将α与d对齐和α与q对齐,一般教科书和论文中以α与d对齐的方式为主,结合之前的clarke仿真波形(等幅值)可以看出,得到的d轴分量为负值,数值大小为abc的幅值,而q轴分量为0。在实际中不同的应用场合会使用不同的方式,MATLAB中以α与q对齐为主。
Park Transform
Inverse Park Transform
park变换在不同的应用中定义有些区别,在电机控制中指的是两相静止坐标系到两相旋转坐标系的转换,而在电网控制中指的是三相静止坐标系到两相旋转坐标系的转换,包含了clarke变换,直接一步到位。
Symmetrical-Components Transform
Inverse Symmetrical-Components Transform

三相系统中还有一种变换,即三相向量到正序向量,负序向量和零序向量的变换,这种在电网中较为常见,在电网发生短路故障时,或者某一相的负载过重,会使得三相电压不平衡。主要是幅值的不平衡和相位的不平衡。正序分量指的是相位和原向量的相序相同,即abc,而负序分量相位与原向量的相序相反,即acb,而零序分量没有相序,均为同一个相角,可以理解为直流。