SSL2644 线段树练习题一【线段树】

线段树

在一类问题中，我们需要经常处理可以映射在一个坐标轴上的一些固定线段，由于线段是可以互相覆盖的，有时需要动态地取线段的并，例如取得并区间的总长度，或者并区间的个数等等。一个线段是对应于一个区间的，因此线段树也可以叫做区间树。

构造思想

线段树是一棵二叉树，树中的每一个结点表示了一个区间$[a,b]$。每一个叶子节点表示了一个单位区间。对于每一个非叶结点所表示的结点$[a,b]$，其左儿子表示的区间为$[a,(a+b)/2]$，右儿子表示的区间为$[(a+b)/2,b]$。

如图为一棵线段树

线段树的运用

线段树的每个节点上往往都增加了一些其他的域。
在这些域中保存了某种动态维护的信息，视不同情况而定。
这些域使得线段树具有极大的灵活性，可以适应不同的需求。

---

简单讲解完线段树后，我们就来看看这道题吧。

思路

可以把题目抽象地描述如下：x轴上有若干条线段，求线段覆盖的总长度。

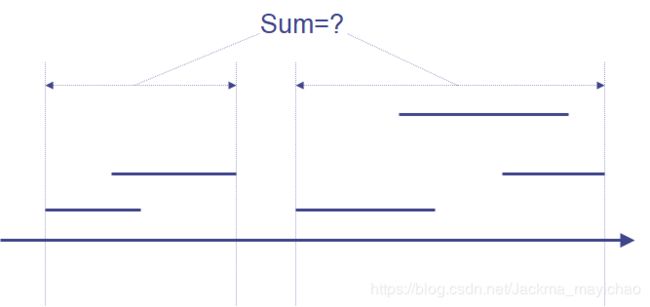
给线段树每个节点增加一个域$cover$。
$cover=1$表示该结点所对应的区间被完全覆盖，
$cover=0$表示该结点所对应的区间未被完全覆盖。

注：此题可以不用先构造出一颗线段树。

构造线段树代码如下：

void build(int x,int ql/*左*/,int qr/*右*/)
   {
   	l[x]=ql; r[x]=qr;
   	if (l[x]==r[x]) return;
   	int mid=(l[x]+r[x])/2;
   	build(x*2,ql,mid); build(x*2+1,mid+1,qr);
   }

正题代码：

#include
#include
#include
#include
using namespace std;
int n,s,l[400010],r[400010];
int tree[400010],ans;
void insert(int x,int l,int r,int a,int b)  //插入
{
	int mid=(l+r)/2;
	if(tree[x]==1)
	  return;
	if(l==a&&r==b)
	  tree[x]=1;
	else if(b<=mid)
	  insert(x*2,l,mid,a,b);
	else if(a>=mid)
	  insert(x*2+1,mid,r,a,b);
	else
	  {
	  	insert(x*2,l,mid,a,mid);
	  	insert(x*2+1,mid,r,mid,b);
	  } 
}
void ccount(int x,int l,int r)   //统计
{
	int mid=(l+r)/2;
	if(tree[x]==1)
	 {
	 	ans+=r-l;
	 	return;
	 }
	if(r-l>1)
	 {
	 	ccount(x*2,l,mid);
	 	ccount(x*2+1,mid,r);
	 }
}
int main()
{
    cin>>s>>n;
    for(int i=1; i<=n; i++)
     {
     	scanf("%d%d",&l[i],&r[i]); 
     	insert(1,1,s,l[i],r[i]);
     }
    ccount(1,1,s);
    cout<<ans;
    return 0;
}