C和C++程序员面试秘笈:33---树的先序遍历、中序遍历、后续遍历、层次遍历（递归与非递归法）
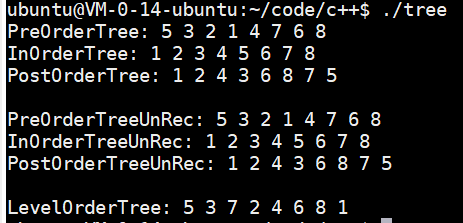
一、先序遍历
递归方法
- 递归的方法比较简单：
- 先打印自己
- 再递归遍历左子树
- 再递归遍历右子树
templatevoid Tree ::PreOrderTree(_TreeNode *node) { if(node != nullptr) { // 先打印自己 std::cout << node->data << " "; // 再遍历左子树 PreOrderTree(node->left); // 再遍历右子树 PreOrderTree(node->right); } }
非递归方法
- 非递归的方法需要用到一个栈来保存临时节点
- 方法如下：
- 打印根节点数据
- 把根节点的right入栈，遍历左子树
- 遍历完左子树返回时，栈顶元素应该为right，出栈，遍历以该指针为根的子树
templatevoid Tree ::PreOrderTreeUnRec(_TreeNode *node) { std::stack<_TreeNode*> _st; _TreeNode *p = node; // 如果节点不为空: 说明还有节点可以判断 // 如果栈不为空: 如果节点为空, 但是栈不为空, 说明要回退了 while(p != nullptr || !_st.empty()) { while(p != nullptr) { // 先打印节点的值, 再将左节点压入栈 std::cout << p->data << " "; _st.push(p); //把遍历的节点全部压栈 p = p->left; } // 栈不为空, 将节点出栈, 然后右节点压入栈 if(!_st.empty()) { p = _st.top(); // 得到栈顶内容 _st.pop(); // 出栈 p = p->right; // 指向右子节点, 下一次循环就会先序遍历左子树 } } }
二、中序遍历
递归方法
- 递归的方法比较简单：
- 先递归遍历左子树
- 再打印自己
- 再递归遍历右子树
templatevoid Tree ::InOrderTree(_TreeNode *node) { if(node != nullptr) { // 先遍历左子树 InOrderTree(node->left); // 再打印自己 std::cout << node->data << " "; // 再遍历右子树 InOrderTree(node->right); } }
非递归方法
- 非递归的方法需要用到一个栈来保存临时节点
- 方法如下：
- 先将根节点入栈，遍历左子树
- 遍历左子树返回时，栈顶元素应该为根节点，此时出栈，并打印节点数据
- 再中序遍历右子树
templatevoid Tree ::InOrderTreeUnRec(_TreeNode *node) { std::stack<_TreeNode*> _st; _TreeNode *p = node; // 如果节点不为空: 说明还有节点可以判断 // 如果栈不为空: 如果节点为空, 但是栈不为空, 说明要回退了 while(p != nullptr || !_st.empty()) { // 逐渐将左节点加入到栈中 while(p != nullptr) { _st.push(p); //把遍历的节点全部压栈 p = p->left; } // 栈不为空, 将节点出栈, 然后右节点压入栈 if(!_st.empty()) { p = _st.top(); // 得到栈顶内容 _st.pop(); // 出栈 std::cout << p->data << " "; p = p->right; // 指定右子节点, 下一次循环时就会中序遍历右子树 } } }
三、后续遍历
递归方法
- 递归的方法比较简单：
- 先递归遍历左子树
- 再递归遍历右子树
- 再打印自己
templatevoid Tree ::PostOrderTree(_TreeNode *node) { if(node != nullptr) { // 先遍历左子树 PostOrderTree(node->left); // 再遍历右子树 PostOrderTree(node->right); // 再打印自己 std::cout << node->data << " "; } }
非递归方法
- 方法为：
- 假设root是要遍历树的根指针，后序遍历要求在遍历完左、右子树再访问根。需要判断根节点的左、右子树是否均遍历过
- 可采用标记法，节点入栈时，配一个标志tag一同入栈（tag为0表示遍历左子树前的现场保护，tag为1表示遍历右子树前的现场保护）
- 首先将root和tag（为0）入栈，遍历左子树；返回后，修改栈顶tag为1，遍历右子树；最后访问根节点
templatevoid Tree ::PostOrderTreeUnRec(_TreeNode *node) { std::stack<_TreeNode*> _st; _TreeNode *p = node; // 如果节点不为空: 说明还有节点可以判断 // 如果栈不为空: 如果节点为空, 但是栈不为空, 说明要回退了 while(p != nullptr || !_st.empty()) { while(p != nullptr) { _st.push(p); //压栈 p = p->left; //遍历左子树 } if(!_st.empty()) { p = _st.top(); //得到栈顶元素 if(p->tag) // tag为1时 { std::cout << p->data << " "; // 打印节点数据 _st.pop(); // 出栈 p = nullptr; // 第二次访问标志其右子树已经遍历过了 } else { p->tag = 1; // 修改tag为1 p = p->right; // 指向右节点, 下次遍历其左子树 } } } }
四、层次遍历
- 假设现在我们有一棵这样的树
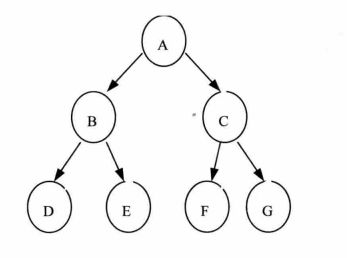
- 层次遍历不能通过节点的指针来实现，需要借助一个队列来实现。方法为：
- A入队
- 此时队列顶部为A，A出队（同时打印A），然后将A的子节点B、C入队（此时队列中有B、C）
- 此时队列顶部为B，B出队（同时打印B），然后将B的子节点D、E入队（此时队列中有C、D、E）
- 此时队列顶部为C，C出队（同时打印C），然后将C的子节点F、G入队（此时队列中有D、E、F、G）
- 此时队列顶部为D，D出队（同时打印D），此时D无子节点，不需要加入任何节点（此时队列中有E、F、G）
- 以此类推，将E、F、G出队（每次出队列时都打印）
- 代码如下：
template
void Tree::LevelOrderTree(_TreeNode *node)
{
std::queue<_TreeNode*> _qu;
_TreeNode *p;
// 先将根节点入队列
_qu.push(root);
while(!_qu.empty())
{
// 获取队首元素, 将队首出队并同时打印
p = _qu.front();
_qu.pop();
std::cout << p->data << " ";
// 如果出队的这个元素的左子节点不为空, 将左子节点队列
if(p->left != nullptr)
_qu.push(p->left);
// 如果出队的这个元素的右子节点不为空, 将右子节点队列
if(p->right != nullptr)
_qu.push(p->right);
}
} 五、测试代码
- 下面是一个二叉搜索树的实现代码，关于二叉搜索树请参阅：https://blog.csdn.net/qq_41453285/article/details/103963343
- 在这个代码中包含了上面我们所有的遍历算法，并在main()函数中进行了测试
/*
* @Description: 二叉搜索树的实现
* @CSDN Link: https://blog.csdn.net/qq_41453285/article/details/107677599
* @Version: 1.0
* @Autor: Dongshao
* @Date: 2020-07-26 08:39:45
* @LastEditors: Dongshao
* @LastEditTime: 2020-07-29 22:55:11
*/
#include
#include
#include
using std::cout;
using std::endl;
// 二叉搜索树
template
class Tree
{
private:
// 树节点
typedef struct treeNode{
treeNode(T _data, struct treeNode *_left, struct treeNode *right) : data(_data), left(_left), right(right) { }
T data; // 节点的数据
int tag; // 节点的一个标志, 只有非递归后续遍历树时才会用到, 其他地方不需要用到
struct treeNode *left;
struct treeNode *right;
}_TreeNode;
private:
// 根节点
_TreeNode *root;
public:
// 构造函数, 使用数组构造一棵二叉搜索树
Tree(T arr[], size_t len);
public:
// 前序遍历
void PreOrderTree()
{
if(root == nullptr)
return;
PreOrderTree(root);
std::cout << std::endl;
}
// 中序遍历
void InOrderTree()
{
if(root == nullptr)
return;
InOrderTree(root);
std::cout << std::endl;
}
// 后续遍历
void PostOrderTree()
{
if(root == nullptr)
return;
PostOrderTree(root);
std::cout << std::endl;
}
// 非递归前序遍历
void PreOrderTreeUnRec()
{
if(root == nullptr)
return;
PreOrderTreeUnRec(root);
std::cout << std::endl;
}
// 非递归中序遍历
void InOrderTreeUnRec()
{
if(root == nullptr)
return;
InOrderTreeUnRec(root);
std::cout << std::endl;
}
// 非递归后续遍历
void PostOrderTreeUnRec()
{
if(root == nullptr)
return;
PostOrderTreeUnRec(root);
std::cout << std::endl;
}
// 层次
void LevelOrderTree()
{
if(root == nullptr)
return;
LevelOrderTree(root);
std::cout << std::endl;
}
private:
void PreOrderTree(_TreeNode *node);
void InOrderTree(_TreeNode *node);
void PostOrderTree(_TreeNode *node);
void PreOrderTreeUnRec(_TreeNode *node);
void InOrderTreeUnRec(_TreeNode *node);
void PostOrderTreeUnRec(_TreeNode *node);
void LevelOrderTree(_TreeNode *node);
private:
// 将一个节点插入刀二叉搜索树中
void insertNode(T elem);
};
template
Tree::Tree(T arr[], size_t len)
{
root = nullptr;
// 循环将节点插入到二叉搜索树中
for(int i = 0; i < len; ++i)
insertNode(arr[i]);
}
template
void Tree::insertNode(T elem)
{
// 创建一个新的节点
_TreeNode *newNode = new _TreeNode(elem, nullptr, nullptr);
// 如果根节点为空, 将其作为根节点
if(root == nullptr)
{
root = newNode;
return;
}
// 指向于根节点
_TreeNode *step = root, *temp;
while(step != nullptr)
{
// 先记录下这个节点
temp = step;
// 如果新节点大于该节点, 向右偏移
if(newNode->data > step->data)
step = step->right;
// 如果新节点小于该节点, 向左偏移
else if(newNode->data < step->data)
step = step->left;
}
// 偏移完成之后, temp一定指向于尾节点, 然后将新节点与尾节点比较, 将其插入左边还是右边
if(temp->data > newNode->data)
temp->left = newNode;
else
temp->right = newNode;
}
template
void Tree::PreOrderTree(_TreeNode *node)
{
if(node != nullptr)
{
// 先打印自己
std::cout << node->data << " ";
// 再遍历左子树
PreOrderTree(node->left);
// 再遍历右子树
PreOrderTree(node->right);
}
}
template
void Tree::InOrderTree(_TreeNode *node)
{
if(node != nullptr)
{
// 先遍历左子树
InOrderTree(node->left);
// 再打印自己
std::cout << node->data << " ";
// 再遍历右子树
InOrderTree(node->right);
}
}
template
void Tree::PostOrderTree(_TreeNode *node)
{
if(node != nullptr)
{
// 先遍历左子树
PostOrderTree(node->left);
// 再遍历右子树
PostOrderTree(node->right);
// 再打印自己
std::cout << node->data << " ";
}
}
template
void Tree::PreOrderTreeUnRec(_TreeNode *node)
{
std::stack<_TreeNode*> _st;
_TreeNode *p = node;
// 如果节点不为空: 说明还有节点可以判断
// 如果栈不为空: 如果节点为空, 但是栈不为空, 说明要回退了
while(p != nullptr || !_st.empty())
{
while(p != nullptr)
{
// 先打印节点的值, 再将左节点压入栈
std::cout << p->data << " ";
_st.push(p); //把遍历的节点全部压栈
p = p->left;
}
// 栈不为空, 将节点出栈, 然后右节点压入栈
if(!_st.empty())
{
p = _st.top(); // 得到栈顶内容
_st.pop(); // 出栈
p = p->right; // 指向右子节点, 下一次循环就会先序遍历左子树
}
}
}
template
void Tree::InOrderTreeUnRec(_TreeNode *node)
{
std::stack<_TreeNode*> _st;
_TreeNode *p = node;
// 如果节点不为空: 说明还有节点可以判断
// 如果栈不为空: 如果节点为空, 但是栈不为空, 说明要回退了
while(p != nullptr || !_st.empty())
{
// 逐渐将左节点加入到栈中
while(p != nullptr)
{
_st.push(p); //把遍历的节点全部压栈
p = p->left;
}
// 栈不为空, 将节点出栈, 然后右节点压入栈
if(!_st.empty())
{
p = _st.top(); // 得到栈顶内容
_st.pop(); // 出栈
std::cout << p->data << " ";
p = p->right; // 指定右子节点, 下一次循环时就会中序遍历右子树
}
}
}
template
void Tree::PostOrderTreeUnRec(_TreeNode *node)
{
std::stack<_TreeNode*> _st;
_TreeNode *p = node;
// 如果节点不为空: 说明还有节点可以判断
// 如果栈不为空: 如果节点为空, 但是栈不为空, 说明要回退了
while(p != nullptr || !_st.empty())
{
while(p != nullptr)
{
_st.push(p); //压栈
p = p->left; //遍历左子树
}
if(!_st.empty())
{
p = _st.top(); //得到栈顶元素
if(p->tag) // tag为1时
{
std::cout << p->data << " "; // 打印节点数据
_st.pop(); // 出栈
p = nullptr; // 第二次访问标志其右子树已经遍历过了
}
else
{
p->tag = 1; // 修改tag为1
p = p->right; // 指向右节点, 下次遍历其左子树
}
}
}
}
template
void Tree::LevelOrderTree(_TreeNode *node)
{
std::queue<_TreeNode*> _qu;
_TreeNode *p;
// 先将根节点入队列
_qu.push(root);
while(!_qu.empty())
{
// 获取队首元素, 将队首出队并同时打印
p = _qu.front();
_qu.pop();
std::cout << p->data << " ";
// 如果出队的这个元素的左子节点不为空, 将左子节点队列
if(p->left != nullptr)
_qu.push(p->left);
// 如果出队的这个元素的右子节点不为空, 将右子节点队列
if(p->right != nullptr)
_qu.push(p->right);
}
}
int main()
{
int arr[] = {5, 3, 7, 2, 4, 6, 8, 1};
Tree *myTree = new Tree(arr, sizeof(arr) / sizeof(int));
// 递归先序、中序、后续遍历
std::cout << "PreOrderTree: ";
myTree->PreOrderTree();
std::cout << "InOrderTree: ";
myTree->InOrderTree();
std::cout << "PostOrderTree: ";
myTree->PostOrderTree();
std::cout << std::endl;
// 非递归先序、中序、后续遍历
std::cout << "PreOrderTreeUnRec: ";
myTree->PreOrderTreeUnRec();
std::cout << "InOrderTreeUnRec: ";
myTree->InOrderTreeUnRec();
std::cout << "PostOrderTreeUnRec: ";
myTree->PostOrderTreeUnRec();
std::cout << std::endl;
// 层次遍历
std::cout << "LevelOrderTree: ";
myTree->LevelOrderTree();
return 0;
} - 我们本次测试的代码二叉搜索树如下所示：
- 代码运行的效果如下，全部正确：
