scala数据结构-树
文章目录
- 数组-链表-树形结构对比
- 树形结构概念
- 特点
- 术语
- 树的种类
- 无序树
- 有序树
- 二叉树
- 性质
- 种类
- 满二叉树(full binary tree)
- 完全二叉树
- 平衡二叉树(AVL树)
- 二叉搜索树
- 遍历二叉树
- 先序遍历 ,中序遍历,后序遍历
- 查找
- 二叉树的删除
- 顺序存储二叉树
- 二叉排序树
- 删除叶子节点
- 删除非叶子节点(非叶子节点只有一个分支)
- 删除非叶子节点(非叶子节点有两个分支)
- 完整版
数组-链表-树形结构对比
数组的优点与缺点
- 优点
通过下标方式访问元素,速度快。对于有序数组,还可使用二分查找提高检索速度。
2.缺点
如果要检索具体某个值,或者插入值(按一定顺序)会整体移动,效率较低
链式存储的优点和缺点
1.优点:
在一定程度上对数组存储方式有优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可)
2.缺点:
在进行检索时,效率仍然较低,比如(检索某个值,需要从头节点开始遍历)
树存储方式分析
能提高数据存储,读取的效率, 比如利用 二叉排序树(Binary Sort Tree),既可以保证数据的检索速度,同时也可以保证数据的插入,删除,修改的速度。
树形结构概念
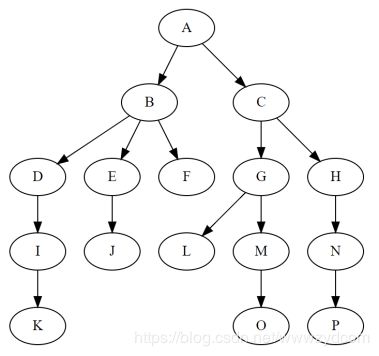
人们更容易理解线性的数据结构(数组, 链表等)而不是树和图这种数据结构。树是非线性数据结构。它们不以线性方式存储数据。他们按层次组织数据.
树(英语:tree)是一种抽象数据类型(ADT: Abstract Data Type)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
特点
1.每个节点都只有有限个子节点或无子节点;
2.没有父节点的节点称为根节点;
3.每一个非根节点有且只有一个父节点;
4.除了根节点外,每个子节点可以分为多个不相交的子树;
5.树里面没有环路(cycle)
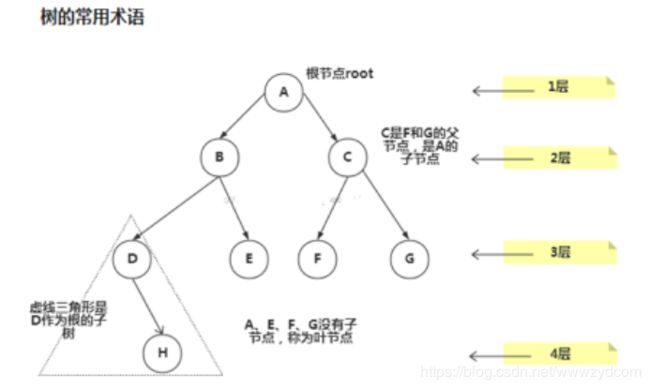
术语
- 节点的度: 一个节点含有的子树的个数称为该节点的度
- 树的度: 一棵树中,最大的节点度称为树的度
- 叶节点:度为0的节点
- 非终端节点或分支节点: 度不为0的节点
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 节点的祖先:从根到该节点所经分支上的所有节点
- 森林:由m(m>=0)棵互不相交的树的集合称为森林
树的种类
无序树
树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
有序树
树中任意节点的子节点之间有顺序关系,这种树称为有序树
- 二叉树:每个节点最多含有两个子树的树称为二叉树
其中二叉树又分为: 完全二叉树,满二叉树,排序二叉树(二叉查找树(英语:Binary Search Tree)),平衡二叉树(AVL树)
- 霍夫曼树
- B 树
二叉树
二叉树每个加点最多有两个子树(即:不存在度大于2的节点),二叉树的子树有左右之分,次序不能颠倒
二叉树有5种基本形态:
1.二叉树可以是空集
2.可以有空的左子树
3.可以有空右子树;
4.左右子树皆为空。
5.左右子树都有
性质
1, 第i层最多有个2^i-1个节点
2,深度为的二叉树的至多有个节点 (根节点的深度是 0 ),深度为的二叉树的至多有个节点 (根节点的深度是 0 )
- 非空的二叉树,若树叶总数为n0,分支度为2的总数为 n2,则n0=n2+1
种类
满二叉树(full binary tree)
层数为k, 有(2^k)-1个节点的二叉树就是满二叉树
1.第层的节点数量是: 2^k-1
2.总节点数: (2^k) -1
完全二叉树
如果二叉树所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续 为完全二叉树
除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点
完全二叉树是效率很高的数据结构,堆是一种完全二叉树,所以效率极高. 在做堆排序的时候, 就是把数组看成一个完全二叉树来对待
平衡二叉树(AVL树)
AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
定义: 这种左右子树的高度相差不超过 1 的树为平衡二叉树。
平衡之意,如天平,即两边的分量大约相同。
二叉搜索树
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树
1.若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2.若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3.任意节点的左、右子树也分别为二叉查找树;
没有键值相等的节点
遍历二叉树
二叉树有3中遍历方式: 先序遍历, 中序遍历,后序遍历,根据父节点先中后顺序依次分为三种遍历顺序
先序遍历 ,中序遍历,后序遍历
先访问根节点,然后访问左节点,最后访问右节点(根->左->右)
package com.zyd
object BinaryTreeDemo {
def main(args: Array[String]): Unit = {
//先用比较简单的方法,直接关联的方法
val root1 = new HeroNode(1, "a1")
val root2 = new HeroNode(2, "b2")
val root3 = new HeroNode(3, "c3")
val root4 = new HeroNode(4, "d4")
val root5 = new HeroNode(5, "e5")
root1.left = root2
root1.right = root3
root3.left = root5
root3.right = root4
println("========前序遍历======")
root1.preOrder()
println("========中序遍历======")
root1.infixOrder()
println("========后序遍历======")
root1.postOrder()
}
}
// 定义节点
class HeroNode(hNo: Int, hName: String) {
val no = hNo
val name = hName
var left: HeroNode = null
var right: HeroNode = null
//前序遍历
def preOrder(): Unit = {
//先输出当前节点值
printf("节点信息: no=%d name=%s \n", no, name)
//向左遍历输出左子树
if (this.left != null) {
this.left.preOrder()
}
//向右边递归输出右子树
if (this.right != null) {
this.right.preOrder()
}
}
//中序遍历
def infixOrder(): Unit ={
//向左遍历输出左子树
if (this.left != null) {
this.left.infixOrder()
}
//输出当前节点值
printf("节点信息: no=%d name=%s \n", no, name)
//向右边递归输出右子树
if (this.right != null) {
this.right.infixOrder()
}
}
//后序遍历
def postOrder(): Unit ={
//向左遍历输出左子树
if (this.left != null) {
this.left.postOrder()
}
//向右边递归输出右子树
if (this.right != null) {
this.right.postOrder()
}
//输出当前节点值
printf("节点信息: no=%d name=%s \n", no, name)
}
}
class BinaryTree {
var root: HeroNode = null
def preOrder(): Unit = {
if (root != null) {
root.preOrder()
} else {
println("当前二叉树为空,不能遍历!")
}
}
}
查找
package com.zyd
object BinaryTreeDemo {
def main(args: Array[String]): Unit = {
//先用比较简单的方法,直接关联的方法
val root1 = new HeroNode(1, "a1")
val root2 = new HeroNode(2, "b2")
val root3 = new HeroNode(3, "c3")
val root4 = new HeroNode(4, "d4")
val root5 = new HeroNode(5, "e5")
root1.left = root2
root1.right = root3
root3.left = root5
root3.right = root4
println("========前序查找======")
val node = root1.preOrder(5)
if (null != node) {
printf("find 编号=%d name=%s", node.no, node.name)
println
} else {
println("not find ...")
}
println("========中序查找======")
val node2 = root1.infixOrder(5)
if (null != node2) {
printf("find 编号=%d name=%s", node2.no, node2.name)
println
} else {
println("not find ...")
}
println("========后序查找======")
val node3 = root1.infixOrder(5)
if (null != node3) {
printf("find 编号=%d name=%s", node3.no, node3.name)
println
} else {
println("not find ...")
}
}
}
// 定义节点
class HeroNode(hNo: Int, hName: String) {
val no = hNo
val name = hName
var left: HeroNode = null
var right: HeroNode = null
//前序查找
def preOrder(no: Int): HeroNode = {
if (no == this.no) {
return this
}
//向左递归查找
var resNode: HeroNode = null
if (this.left != null) {
resNode = this.left.preOrder(no)
}
if (resNode != null) {
return resNode
}
//向右递归查找
if (this.right != null) {
resNode = this.right.preOrder(no)
}
return resNode
}
//中序查找
def infixOrder(no: Int): HeroNode = {
var resNode: HeroNode = null
//向左递归查找
if (this.left != null) {
resNode = this.left.infixOrder(no)
}
if (resNode != null) {
return resNode
}
if (no == this.no) {
return this
}
//向右递归查找
if (this.right != null) {
resNode = this.right.infixOrder(no)
}
return resNode
}
//后序遍历
def postOrder(no: Int): HeroNode = {
var resNode: HeroNode = null
if (this.left != null) {
resNode = this.left.postOrder(no)
}
if (resNode != null){
return resNode
}
if (this.right != null){
resNode = this.right.preOrder(no)
}
if (resNode != null){
return resNode
}
if (this.no == no){
return this
}
resNode
}
}
class BinaryTree {
var root: HeroNode = null
def preOrder(no: Int): HeroNode = {
if (root != null) {
root.preOrder(no)
} else {
println("当前二叉树为空,不能遍历!")
return null
}
}
def preOrderSearch(no: Int): HeroNode = {
if (root != null) {
return root.preOrder(no)
} else {
return null
}
}
def infixOrderSearch(no: Int): HeroNode = {
if (root != null) {
root.infixOrder(no)
} else {
println("当前二叉树为空,不能遍历!")
return null
}
}
def postOrderSearch(no: Int): HeroNode = {
if (root != null) {
root.postOrder(no)
} else {
println("当前二叉树为空,不能遍历!")
return null
}
}
}
二叉树的删除
(1) 如果删除的节点是叶子节点,删除该节点
(2)删除的节点是非叶子节点,则删除该子树
package com.zyd
object BinaryTreeDemo {
def main(args: Array[String]): Unit = {
//先用比较简单的方法,直接关联的方法
val root1 = new HeroNode(1, "a1")
val root2 = new HeroNode(2, "b2")
val root3 = new HeroNode(3, "c3")
val root4 = new HeroNode(4, "d4")
val root5 = new HeroNode(5, "e5")
root1.left = root2
root1.right = root3
root3.left = root5
root3.right = root4
}
}
// 定义节点
class HeroNode(hNo: Int, hName: String) {
val no = hNo
val name = hName
var left: HeroNode = null
var right: HeroNode = null
def delNode(no: Int): Unit = {
//首先比较当前节点的左子节点是否为要删除的节点
if (this.left != null && this.left.no == no) {
this.left = null
return
}
//比较当前节点的右子节点是否为要删除的节点
if (this.right != null && this.right.no == no) {
this.right = null
return
}
//向左递归删除
if (this.left != null) {
this.left.delNode(no)
}
//向右递归删除
if (this.right != null) {
this.right.delNode(no)
}
}
}
class BinaryTree {
var root: HeroNode = null
def delNode(no: Int): Unit = {
if (root != null) {
//先处理下root是不是删除的
if (root.no == no) {
root = null
} else {
root.delNode(no)
}
}
}
}
顺序存储二叉树
基本说明
对于数据存储,数组存储的方式可以看做树,树也可以看做数组存储
场景 给定 val arr = Array(1, 2, 3, 4, 5, 6) 实现前序遍历
package com.zyd
object ArrayTreeDemo {
def main(args: Array[String]): Unit = {
val arr = Array(1, 2, 3, 4, 5, 6)
val tree = new ArrayTree(arr)
tree.preOrder()
}
}
class ArrayTree(val arr: Array[Int]) {
def preOrder(): Unit = {
this.preOrder(0)
}
def preOrder(index: Int): Unit = {
if (arr == null || arr.length == 0) {
println("数组为空,不能按照二叉树前序遍历")
}
println(arr(index))
//向左递归遍历
if ((index * 2 + 1) < arr.length) {
preOrder(index * 2 + 1)
}
//向右递归遍历
if ((index * 2 + 2) < arr.length) {
preOrder(index * 2 + 2)
}
}
}
二叉排序树
BST(Binary Sort Tree): 对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大
特别说明:相同的值可以放左边或右边
案例: 一个数组创建对应的二叉排序树,并使用中序遍历二叉排序树
package com.zyd
object Array2BinaryTree {
def main(args: Array[String]): Unit = {
val arr = Array(10, 5, 6, 1, 45, 3, 8)
val tee = new BinarySortTee
for (item <- arr){
tee.add(new Node(item))
}
//遍历二叉树
tee.infixOrder()
}
}
class Node(var value: Int) {
var left: Node = null
var right: Node = null
//添加方法
def add(node: Node): Unit = {
if (node == null) { //节点为空,返回
return
}
//如果插入的节点值小于当前节点的值
if (node.value < this.value) {
if (this.left == null) {
//说明该节点下没有左子节点
this.left = node
} else {
//递归进行插入
this.left.add(node)
}
} else {
//如果插入的节点值不小于当前节点的值
if (this.right == null) {
this.right = node
} else {
//递归进行插入
this.right.add(node)
}
}
}
//中序遍历
def infixOrder(): Unit = {
//向左递归遍历输出左子树
if (this.left != null) {
this.left.infixOrder()
}
//先输出当前节点值
printf("value=>"+ this.value+" ")
if (this.right != null) {
this.right.infixOrder()
}
}
}
//定义我们的二叉排序树
class BinarySortTee {
var root: Node = null
def add(node: Node): Unit = {
if (root == null) {
root = node
} else {
root.add(node)
}
}
//中序遍历
def infixOrder(): Unit = {
if (root != null) {
root.infixOrder()
} else {
println("当前二叉树为空,不能遍历")
}
}
}
结果
value=>1 value=>3 value=>5 value=>6 value=>8 value=>10 value=>45
删除叶子节点
1.检索要删除的节点,没找到就退出
2.检索到要删除的节点,需要找到该节点的父节点的叶子节点指向null
package com.zyd
object Array2BinaryTree {
def main(args: Array[String]): Unit = {
val arr = Array(7 ,3, 10, 12, 1, 9, 2)
val tee = new BinarySortTee
for (item <- arr) {
tee.add(new Node(item))
}
//遍历二叉树
tee.infixOrder()
tee.delNode(2)
println("delete....")
tee.infixOrder()
}
}
class Node(var value: Int) {
var left: Node = null
var right: Node = null
//添加方法
def add(node: Node): Unit = {
if (node == null) { //节点为空,返回
return
}
//如果插入的节点值小于当前节点的值
if (node.value < this.value) {
if (this.left == null) {
//说明该节点下没有左子节点
this.left = node
} else {
//递归进行插入
this.left.add(node)
}
} else {
//如果插入的节点值不小于当前节点的值
if (this.right == null) {
this.right = node
} else {
//递归进行插入
this.right.add(node)
}
}
}
//中序遍历
def infixOrder(): Unit = {
//向左递归遍历输出左子树
if (this.left != null) {
this.left.infixOrder()
}
//先输出当前节点值
printf("value=>" + this.value + " ")
if (this.right != null) {
this.right.infixOrder()
}
}
//根据值查找某个节点
def search(value: Int): Node = {
//先判断当前接待您是否为要删除的节点
if (value == this.value) {
return this
} else if (value < this.value) { //向左递归查找
if (this.left == null) {
return null
} else {
return this.left.search(value)
}
} else {
if (this.right == null) {
return null
} else {
return this.right.search(value)
}
}
}
//根据值找到某个节点的父节点
def searchParent(value: Int): Node = {
//1. 先判断当前节点的左子节点或右子节点是否是这个值
if ((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)
) {
return this
}
else {
//向左递归查找
if (this.left != null && value < this.value) {
return this.left.searchParent(value)
} else if (this.right != null && value > this.value) {
return this.right.searchParent(value)
} else {
return null
}
}
}
}
//定义我们的二叉排序树
class BinarySortTee {
var root: Node = null
def add(node: Node): Unit = {
if (root == null) {
root = node
} else {
root.add(node)
}
}
//中序遍历
def infixOrder(): Unit = {
if (root != null) {
root.infixOrder()
} else {
println("当前二叉树为空,不能遍历")
}
}
//查找节点
def search(value: Int): Node = {
if (root != null) {
return root.search(value)
} else {
return null
}
}
//查找父节点
def searchParent(value: Int): Node = {
if (root != null) {
return root.searchParent(value)
} else {
return null
}
}
//删除节点
def delNode(value: Int): Unit = {
if (root == null) {
//空树不删除
return null
}
//先看有没有要删除的节点
val targetNode = search(value)
if (targetNode == null) { //没有要删除的节点,直接返回
return
} else {
//查找 targetNode 的父节点
var parentNode = searchParent(value)
//叶子节点
if (targetNode.left == null && targetNode.right == null){
//判断targetNode 是 parentNode 的左子节点还是右子节点
if (parentNode.left != null && parentNode.left.value == value){
parentNode.left = null
}else{
parentNode.right = null
}
}
}
}
}
结果
value=>1 value=>2 value=>3 value=>7 value=>9 value=>10 value=>12
delete…
value=>1 value=>3 value=>7 value=>9 value=>10 value=>12
删除非叶子节点(非叶子节点只有一个分支)
package com.zyd
object Array2BinaryTree {
def main(args: Array[String]): Unit = {
val arr = Array(7, 3, 10, 12, 1, 9, 2)
val tee = new BinarySortTee
for (item <- arr) {
tee.add(new Node(item))
}
//遍历二叉树
tee.infixOrder()
tee.delNode(1)
println("\ndelete....")
tee.infixOrder()
}
}
class Node(var value: Int) {
var left: Node = null
var right: Node = null
//添加方法
def add(node: Node): Unit = {
if (node == null) { //节点为空,返回
return
}
//如果插入的节点值小于当前节点的值
if (node.value < this.value) {
if (this.left == null) {
//说明该节点下没有左子节点
this.left = node
} else {
//递归进行插入
this.left.add(node)
}
} else {
//如果插入的节点值不小于当前节点的值
if (this.right == null) {
this.right = node
} else {
//递归进行插入
this.right.add(node)
}
}
}
//中序遍历
def infixOrder(): Unit = {
//向左递归遍历输出左子树
if (this.left != null) {
this.left.infixOrder()
}
//先输出当前节点值
printf("value=>" + this.value + " ")
if (this.right != null) {
this.right.infixOrder()
}
}
//根据值查找某个节点
def search(value: Int): Node = {
//先判断当前接待您是否为要删除的节点
if (value == this.value) {
return this
} else if (value < this.value) { //向左递归查找
if (this.left == null) {
return null
} else {
return this.left.search(value)
}
} else {
if (this.right == null) {
return null
} else {
return this.right.search(value)
}
}
}
//根据值找到某个节点的父节点
def searchParent(value: Int): Node = {
//1. 先判断当前节点的左子节点或右子节点是否是这个值
if ((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)
) {
return this
}
else {
//向左递归查找
if (this.left != null && value < this.value) {
return this.left.searchParent(value)
} else if (this.right != null && value > this.value) {
return this.right.searchParent(value)
} else {
return null
}
}
}
}
//定义我们的二叉排序树
class BinarySortTee {
var root: Node = null
def add(node: Node): Unit = {
if (root == null) {
root = node
} else {
root.add(node)
}
}
//中序遍历
def infixOrder(): Unit = {
if (root != null) {
root.infixOrder()
} else {
println("当前二叉树为空,不能遍历")
}
}
//查找节点
def search(value: Int): Node = {
if (root != null) {
return root.search(value)
} else {
return null
}
}
//查找父节点
def searchParent(value: Int): Node = {
if (root != null) {
return root.searchParent(value)
} else {
return null
}
}
//删除节点
def delNode(value: Int): Unit = {
if (root == null) {
//空树不删除
return null
}
//先看有没有要删除的节点
val targetNode = search(value)
if (targetNode == null) { //没有要删除的节点,直接返回
return
} else {
//查找 targetNode 的父节点
var parentNode = searchParent(value)
//叶子节点
if (targetNode.left == null && targetNode.right == null) {
//判断targetNode 是 parentNode 的左子节点还是右子节点
if (parentNode.left != null && parentNode.left.value == value) {
parentNode.left = null
} else {
parentNode.right = null
}
} else if (targetNode.left != null && targetNode.right != null){
//targetNode 只有两个节点
}else {
//targetNode 只有一个节点
//判断targetNode是parentNode的左子节点还是右子节点
if (targetNode.left != null){ //要删除的节点的左子节点不为空
//判断targetNode 是parentNode 的左还是右
if (parentNode.left.value == value){
parentNode.left = targetNode.left
}else{
parentNode.right = targetNode.left
}
} else { //目标节点右子节点不为空
if (parentNode.left.value == value){
parentNode.left = targetNode.right
}else{
parentNode.right = targetNode.right
}
}
}
}
}
}
删除非叶子节点(非叶子节点有两个分支)
思路:找到要删除节点的右子树里的最小值,删除其最小值并替换到当前要删除的值上
package com.zyd
object Array2BinaryTree {
def main(args: Array[String]): Unit = {
val arr = Array(7, 3, 10, 12, 1, 9, 2)
val tee = new BinarySortTee
for (item <- arr) {
tee.add(new Node(item))
}
//遍历二叉树
tee.infixOrder()
tee.delNode(7)
println("\ndelete....")
tee.infixOrder()
}
}
class Node(var value: Int) {
var left: Node = null
var right: Node = null
//添加方法
def add(node: Node): Unit = {
if (node == null) { //节点为空,返回
return
}
//如果插入的节点值小于当前节点的值
if (node.value < this.value) {
if (this.left == null) {
//说明该节点下没有左子节点
this.left = node
} else {
//递归进行插入
this.left.add(node)
}
} else {
//如果插入的节点值不小于当前节点的值
if (this.right == null) {
this.right = node
} else {
//递归进行插入
this.right.add(node)
}
}
}
//中序遍历
def infixOrder(): Unit = {
//向左递归遍历输出左子树
if (this.left != null) {
this.left.infixOrder()
}
//先输出当前节点值
printf("value=>" + this.value + " ")
if (this.right != null) {
this.right.infixOrder()
}
}
//根据值查找某个节点
def search(value: Int): Node = {
//先判断当前接待您是否为要删除的节点
if (value == this.value) {
return this
} else if (value < this.value) { //向左递归查找
if (this.left == null) {
return null
} else {
return this.left.search(value)
}
} else {
if (this.right == null) {
return null
} else {
return this.right.search(value)
}
}
}
//根据值找到某个节点的父节点
def searchParent(value: Int): Node = {
//1. 先判断当前节点的左子节点或右子节点是否是这个值
if ((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)
) {
return this
}
else {
//向左递归查找
if (this.left != null && value < this.value) {
return this.left.searchParent(value)
} else if (this.right != null && value > this.value) {
return this.right.searchParent(value)
} else {
return null
}
}
}
}
//定义我们的二叉排序树
class BinarySortTee {
var root: Node = null
def add(node: Node): Unit = {
if (root == null) {
root = node
} else {
root.add(node)
}
}
//中序遍历
def infixOrder(): Unit = {
if (root != null) {
root.infixOrder()
} else {
println("当前二叉树为空,不能遍历")
}
}
//查找节点
def search(value: Int): Node = {
if (root != null) {
return root.search(value)
} else {
return null
}
}
//查找父节点
def searchParent(value: Int): Node = {
if (root != null) {
return root.searchParent(value)
} else {
return null
}
}
//删除节点
def delNode(value: Int): Unit = {
if (root == null) {
//空树不删除
return null
}
//先看有没有要删除的节点
val targetNode = search(value)
if (targetNode == null) { //没有要删除的节点,直接返回
return
} else {
//查找 targetNode 的父节点
var parentNode = searchParent(value)
//叶子节点
if (targetNode.left == null && targetNode.right == null) {
//判断targetNode 是 parentNode 的左子节点还是右子节点
if (parentNode.left != null && parentNode.left.value == value) {
parentNode.left = null
} else {
parentNode.right = null
}
} else if (targetNode.left != null && targetNode.right != null) {
//targetNode 只有两个节点
val value = delRightTreeMin(targetNode.right)
targetNode.value = value
} else {
//targetNode 只有一个节点
//判断targetNode是parentNode的左子节点还是右子节点
if (targetNode.left != null) { //要删除的节点的左子节点不为空
//判断targetNode 是parentNode 的左还是右
if (parentNode.left.value == value) {
parentNode.left = targetNode.left
} else {
parentNode.right = targetNode.left
}
} else { //目标节点右子节点不为空
if (parentNode.left.value == value) {
parentNode.left = targetNode.right
} else {
parentNode.right = targetNode.right
}
}
}
}
}
def delRightTreeMin(node: Node): Int = {
var target = node
//使用while选混找到右子树的最小值
while (target.left != null) {
//为什么targetNode只遍历是left,如果left无值,right有值呢 答案:存储的二叉树是有序的,因此不存在right有,left无
target = target.left
}
val minValue = target.value
// 删除最小值对应的节点
delNode(minValue)
return minValue
}
}
完整版
package com.zyd
object Array2BinaryTree {
def main(args: Array[String]): Unit = {
val arr = Array(7, 3, 10, 12, 1, 9, 2)
val tee = new BinarySortTee
for (item <- arr) {
tee.add(new Node(item))
}
//遍历二叉树
tee.infixOrder()
tee.delNode(7)
println("\ndelete....")
tee.infixOrder()
}
}
class Node(var value: Int) {
var left: Node = null
var right: Node = null
//添加方法
def add(node: Node): Unit = {
if (node == null) { //节点为空,返回
return
}
//如果插入的节点值小于当前节点的值
if (node.value < this.value) {
if (this.left == null) {
//说明该节点下没有左子节点
this.left = node
} else {
//递归进行插入
this.left.add(node)
}
} else {
//如果插入的节点值不小于当前节点的值
if (this.right == null) {
this.right = node
} else {
//递归进行插入
this.right.add(node)
}
}
}
//中序遍历
def infixOrder(): Unit = {
//向左递归遍历输出左子树
if (this.left != null) {
this.left.infixOrder()
}
//先输出当前节点值
printf("value=>" + this.value + " ")
if (this.right != null) {
this.right.infixOrder()
}
}
//根据值查找某个节点
def search(value: Int): Node = {
//先判断当前接待您是否为要删除的节点
if (value == this.value) {
return this
} else if (value < this.value) { //向左递归查找
if (this.left == null) {
return null
} else {
return this.left.search(value)
}
} else {
if (this.right == null) {
return null
} else {
return this.right.search(value)
}
}
}
//根据值找到某个节点的父节点
def searchParent(value: Int): Node = {
//1. 先判断当前节点的左子节点或右子节点是否是这个值
if ((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)
) {
return this
}
else {
//向左递归查找
if (this.left != null && value < this.value) {
return this.left.searchParent(value)
} else if (this.right != null && value > this.value) {
return this.right.searchParent(value)
} else {
return null
}
}
}
}
//定义我们的二叉排序树
class BinarySortTee {
var root: Node = null
def add(node: Node): Unit = {
if (root == null) {
root = node
} else {
root.add(node)
}
}
//中序遍历
def infixOrder(): Unit = {
if (root != null) {
root.infixOrder()
} else {
println("当前二叉树为空,不能遍历")
}
}
//查找节点
def search(value: Int): Node = {
if (root != null) {
return root.search(value)
} else {
return null
}
}
//查找父节点
def searchParent(value: Int): Node = {
if (root != null) {
return root.searchParent(value)
} else {
return null
}
}
//删除节点
def delNode(value: Int): Unit = {
if (root == null) {
//空树不删除
return null
}
//先看有没有要删除的节点
val targetNode = search(value)
if (targetNode == null) { //没有要删除的节点,直接返回
return
} else {
//查找 targetNode 的父节点
var parentNode = searchParent(value)
//防止只有一个节点现象
if (parentNode == null){
root = null
return
}
//叶子节点
if (targetNode.left == null && targetNode.right == null) {
//判断targetNode 是 parentNode 的左子节点还是右子节点
if (parentNode.left != null && parentNode.left.value == value) {
parentNode.left = null
} else {
parentNode.right = null
}
} else if (targetNode.left != null && targetNode.right != null) {
//targetNode 只有两个节点
val value = delRightTreeMin(targetNode.right)
targetNode.value = value
} else {
//targetNode 只有一个节点
//判断targetNode是parentNode的左子节点还是右子节点
if (targetNode.left != null) { //要删除的节点的左子节点不为空
//判断targetNode 是parentNode 的左还是右
if (parentNode.left.value == value) {
parentNode.left = targetNode.left
} else {
parentNode.right = targetNode.left
}
} else { //目标节点右子节点不为空
if (parentNode.left.value == value) {
parentNode.left = targetNode.right
} else {
parentNode.right = targetNode.right
}
}
}
}
}
def delRightTreeMin(node: Node): Int = {
var target = node
//使用while选混找到右子树的最小值
while (target.left != null) {
//为什么targetNode只遍历是left,如果left无值,right有值呢 答案:存储的二叉树是有序的,因此不存在right有,left无
target = target.left
}
val minValue = target.value
// 删除最小值对应的节点
delNode(minValue)
return minValue
}
}