整理:数据结构与算法之归并排序(递归的虚拟机栈帧的演示)
目录
1、基本思想
2、归并的实例:A-B两个有序数组归并
3、递归:分解一个无需数组,然后归并
3.1 递归分析
3.2 虚拟机栈:演示递归的执行过程(重点)
4、算法分析
1、基本思想
分析归并排序之前,我们先来了解一下分治算法。
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。
分治算法的一般步骤:
- 分解,将要解决的问题划分成若干规模较小的同类问题;
- 求解,当子问题划分得足够小时,用较简单的方法解决;
- 合并,按原问题的要求,将子问题的解逐层合并构成原问题的解。
归并排序是分治算法的典型应用。
归并排序先将一个无序的N长数组切成N个有序子序列(只有一个数据的序列认为是有序序列),然后两两合并,再将合并后的N/2(或者N/2 + 1)个子序列继续进行两两合并,以此类推得到一个完整的有序数组。过程如下图所示:
2、归并的实例:A-B两个有序数组归并
归并排序的核心思想是将两个有序的数组归并到另一个数组中,所以需要开辟额外的空间。
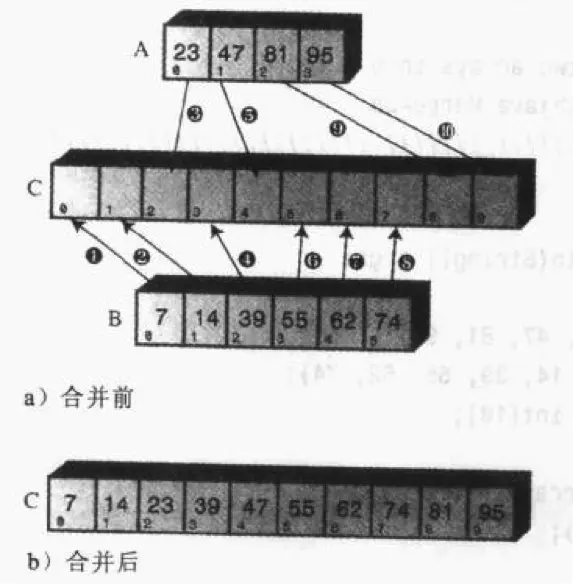
第一步要理清归并的思路。假设现在有两个有序数组A和B,要将两者有序地归并到数组C中。我们用一个实例来推演:
上图中,
A数组中有四个元素,B数组中有六个元素,
首先比较A、B中的第一个元素,将较小的那个放到C数组的第一位,因为该元素就是A、B所有元素中最小的。
上例中,7小于23,所以将7放到了C中。
然后,用23与B中的其他元素比较,如果小于23,继续按顺序放到C中;如果大于23,则将23放入C中。
23放入C中之后,用23之后的47作为基准元素,与B中的其他元素继续比较,重复上面的步骤。
如果有一个数组的元素已经全部复制到C中了,那么将另一个数组中的剩余元素依次插入C中即可。
至此结束。
按照上面的思路,用java实现:
/**
*
* - 归并arrayA与arrayB到arrayC中
*
* - @param arrayA 待归并的数组A
*
* - @param sizeA 数组A的长度
*
* - @param arrayB 待归并的数组B
*
* - @param sizeB 数组B的长度
*
* - @param arrayC 辅助归并排序的数组
*/
public static void merge(int[] arrayA, int sizeA, int[] arrayB, int sizeB, int[] arrayC) {
int i = 0, j = 0, k = 0; // 分别当作arrayA、arrayB、arrayC的下标指针
while (i < sizeA && j < sizeB) { // 两个数组都不为空
if (arrayA[i] < arrayB[j]) { // 将两者较小的那个放到arrayC中
arrayC[k++] = arrayA[i++];
} else {
arrayC[k++] = arrayB[j++];
}
} // 该循环结束后,一个数组已经完全复制到arrayC中了,另一个数组中还有元素
// 后面的两个while循环用于处理另一个不为空的数组
while (i < sizeA) {
arrayC[k++] = arrayA[i++];
}
while (j < sizeB) {
arrayC[k++] = arrayA[j++];
}
for (int l = 0; l < arrayC.length; l++) { // 打印新数组中的元素
System.out.print(arrayC[l] + "\t");
}
}
3、递归:分解一个无序数组,然后归并
再归并之前,还有一步工作需要提前做好,就是数组的分解,可以通过递归的方法来实现。递归(Recursive)是算法设计中常用的思想。
这样通过先递归的分解数组,再合并数组就完成了归并排序。完整的java代码如下:
public class Sort {
private int[] array; // 待排序的数组
public Sort(int[] array) {
this.array = array;
}
// 按顺序打印数组中的元素
public void display() {
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + "\t");
}
System.out.println();
}
// 归并排序
public void mergeSort() {
int[] workSpace = new int[array.length]; // 用于辅助排序的数组
recursiveMergeSort(workSpace, 0, workSpace.length - 1);
}
/**
*
* - 递归的归并排序
*
* - @param workSpace 辅助排序的数组
*
* - @param lowerBound 欲归并数组段的最小下标
*
* - @param upperBound 欲归并数组段的最大下标
*/
private void recursiveMergeSort(int[] workSpace, int lowerBound, int upperBound) {
if (lowerBound == upperBound) { // 该段只有一个元素,不用排序
return;
} else {
int mid = (lowerBound + upperBound) / 2;
recursiveMergeSort(workSpace, lowerBound, mid); // 对低位段归并排序
recursiveMergeSort(workSpace, mid + 1, upperBound); // 对高位段归并排序
merge(workSpace, lowerBound, mid, upperBound);
display();
}
}
/**
*
* - 对数组array中的两段进行合并,lowerBound~mid为低位段,mid+1~upperBound为高位段
*
* - @param workSpace 辅助归并的数组,容纳归并后的元素
*
* - @param lowerBound 合并段的起始下标
*
* - @param mid 合并段的中点下标
*
* - @param upperBound 合并段的结束下标
*/
private void merge(int[] workSpace, int lowerBound, int mid, int upperBound) {
int lowBegin = lowerBound; // 低位段的起始下标
int lowEnd = mid; // 低位段的结束下标
int highBegin = mid + 1; // 高位段的起始下标
int highEnd = upperBound; // 高位段的结束下标
int j = 0; // workSpace的下标指针
int n = upperBound - lowerBound + 1; // 归并的元素总数
while (lowBegin <= lowEnd && highBegin <= highEnd) {
if (array[lowBegin] < array[highBegin]) { // 将两者较小的那个放到workSpace中
workSpace[j++] = array[lowBegin++];
} else {
workSpace[j++] = array[highBegin++];
}
}
while (lowBegin <= lowEnd) {
workSpace[j++] = array[lowBegin++];
}
while (highBegin <= highEnd) {
workSpace[j++] = array[highBegin++];
}
for (j = 0; j < n; j++) { // 将归并好的元素复制到array中
array[lowerBound++] = workSpace[j];
}
}
}
用以下代码测试:
int [] a = {6,2,7,4,8,1,5,3};
Sort sort = new Sort(a);
sort.mergeSort();
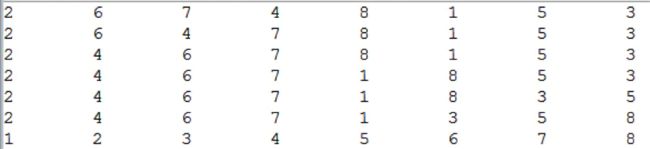
打印结果如下:
3.1 递归分析
归并的顺序是这样的:先将初始数组分为两部分,先归并低位段,再归并高位段。对低位段与高位段继续分解,低位段分解为更细分的一对低位段与高位段,高位段同样分解为更细分的一对低位段与高位段,依次类推。
上例中,
第一步,归并的是 [6与2],
第二步归并的是 [7和4] ,
第三部归并的是前两步归并好的子段 [2,6]与[4,7],
至此,数组的左半部分(低位段)归并完毕,得到[2,4,6,7] ,然后归并右半部分(高位段)。
所以第四步归并的是 [8与1],
第五部归并的是 [5与3],
第六步归并的是前两步归并好的字段 [1,8]与[3,5],
至此,数组的右半部分归并完毕,右边得到 [1,3,5,8]
最后一步就是归并数组的 左半部分[2,4,6,7] 与 右半部分[1,3,5,8]。
归并排序结束。
在本文开始对归并排序的描述中,第一躺归并是对所有相邻的两个元素归并结束之后,才进行下一轮归并,并不是先归并左半部分,再归并右半部分,但是程序的执行顺序与我们对归并排序的分析逻辑不一致,所以理解起来有些困难。
3.2 虚拟机栈:演示递归的执行过程(重点)
先参考:算法设计方法:递归的内涵与经典应用
下面结合代码与图例来详细分析一下归并排序的过程。
虚拟机栈(VM Stack)是描述Java方法执行的内存模型,每一次方法的调用都伴随着一次压栈、出栈操作。
我们要排序的数组为:
int [] a = {6,2,7,4,8,1,5,3}
当main()方法调用mergeSort()方法时,被调用的方法被压入栈中,然后程序进入mergeSort()方法:
public void mergeSort() {
int[] workSpace = new int[array.length]; // 用于辅助排序的数组
recursiveMergeSort(workSpace, 0, workSpace.length - 1);
}
此时,mergeSort()又调用了recursiveMergeSort(workSpace,0,7)方法,recursiveMergeSort(workSpace,0,7)方法也被压入栈中,在mergeSort()之上。
然后,程序进入到 递去①:recursiveMergeSort(workSpace,0,7) 方法:
if (lowerBound == upperBound) { // 该段只有一个元素,不用排序
return;
} else {
int mid = (lowerBound + upperBound) / 2;
recursiveMergeSort(workSpace, lowerBound, mid); // 对低位段归并排序
recursiveMergeSort(workSpace, mid + 1, upperBound); // 对高位段归并排序
merge(workSpace, lowerBound, mid, upperBound);
display();
}
lowerBound参数值为0,upperBound参数值为7,不满足lowerBound == upperBound的条件,所以方法进入else分支,
然后调用方法 recursiveMergeSort(workSpace,0,3),
递去②:recursiveMergeSort(workSpace,0,3) 被压入栈中,此时栈的状态如下:
然而,recursiveMergeSort(workSpace,0,3)不能立即返回,
它在内部又会调用 递去③:recursiveMergeSort(workSpace,0,1),
recursiveMergeSort(workSpace,0,1)又调用了 递去④:recursiveMergeSort(workSpace,0,0),
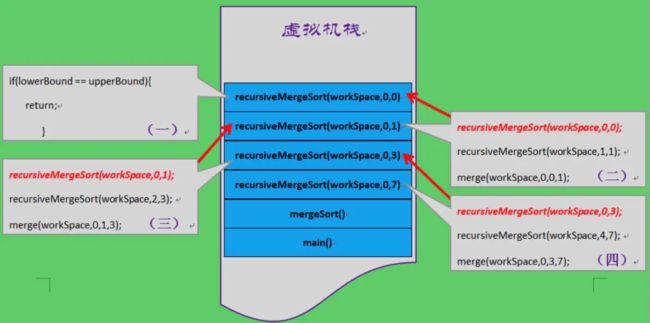
此时,栈中的状态如下:
程序运行到这里,终于有一个方法可以返回了结果了—— 满足终止条件①: recursiveMergeSort(workSpace,0,0),
该方法的执行的逻辑是对数组中的下标从0到0的元素进行归并,该段只有一个元素,所以不用归并,立即return。
方法一旦return,就意味着方法结束,recursiveMergeSort(workSpace,0,0)从栈中弹出。
这时候,程序跳到了代码片段(二)中的第二行: 满足终止条件②:recursiveMergeSort(workSpace,1,1),该方法入栈,recursiveMergeSort(workSpace,0,0)类似,不用归并,直接返回,方法出栈。
这时候程度跳到了代码片段(二)中的第三行:归来时处理:merge(workSpace,0,0,1),即对数组中的前两个元素进行合并(自然,merge(workSpace,0,0,1)也伴随着一次入栈与出栈)。
至此,代码片段(二)执行完毕,归来①:recursiveMergeSort(workSpace,0,1)方法出栈,程序跳到代码片段(三)的第二行:recursiveMergeSort(workSpace,2,3)=> 递去+归来,然在归来时merge(2,2,3)第三和第四个元素,该方法是对数组中的第三个、第四个元素进行归并,与执行recursiveMergeSort(workSpace,0,1)的过程类似,最终会将第三个、第四个元素归并排序。
然后,程序跳到程序跳到代码片段(三)的第三行:merge(workSpace,0,1,3),
将前面已经排好序的两个子序列(【第一第二】个元素为一组、【第三第四】个元素为一组)合并。
然后recursiveMergeSort(workSpace,0,3)出栈,程序跳到代码片段(四)的第二行:recursiveMergeSort(workSpace,4,7),对数组的右半部分的四个元素进行归并排序,伴随着一系列的入栈、出栈,最后将后四个元素排好。此时,数组的左半部分与右半部分已经有序。
然后程序跳到代码片段(四)第三行:merge(workSpace,0,3,7),对数组的左半部分与右半部分合并。
然后recursiveMergeSort(workSpace,4,7)出栈,mergeSort()出栈,最后main()方法出栈,程序结束。
4、算法分析
先来分析一下复制的次数。
如果待排数组有8个元素,归并排序需要分3层,
第一层有四个包含两个数据项的子数组,第二层包含两个包含四个数据项的子数组,
第三层包含一个 8个数据项的数组。合并子数组的时候,每一层的所有元素都要经历一次复制(从原数组复制到workSpace数组),复制总次数为3* 8=24次,即:层数乘以元素总数。
设元素总数为N,则层数为log2N,复制总次数为N log2N。
其实,除了从原数组复制到workSpace数组,还需要从workSpace数组复制到原数组,所以,最终的复制复制次数为2Nlog2N。
在大O表示法中,常数可以忽略,所以归并排序的时间复杂度为O(N log2N)。
一般来讲,复制操作的时间消耗要远大于比较操作的时间消耗,时间复杂度是由复制次数主导的。
下面我们再来分析一下比较次数。
在归并排序中,比较次数总是比复制次数少一些。现在给定两个各有四个元素的子数组,首先来看一下最坏情况和最好情况下的比较次数为多少。
第一种情况,数据项大小交错,所以必须进行7次比较,第二种情况中,一个数组比另一个数组中的所有元素都要小,因此只需要4次比较。
当归并两个子数组时,如果元素总数为N,则最好情况下的比较次数为N/2,最坏情况下的比较次数为N-1。
假设待排数组的元素总数为N,则第一层需要N/2次归并,每次归并的元素总数为2;则第一层需要N/4次归并,每次归并的元素总数为4;则第一层需要N/8次归并,每次归并的元素总数为8……最后一次归并次数为1,归并的元素总数为N。总层数为log2N。
最好情况下的比较总数为:
N/2*(2/2)+ N/4*(4/2)+ N/8*(8/2)+...+1*(N/2) = (N/2)*log2N
最好情况下的比较总数为:
N/2*(2-1)+ N/4*(4-1)+ N/8*(8-1)+...+1*(N-1) = (N-N/2)+ (N-N/4)+(N-N/8)+...+(N-1) = N*log2N-(1+ N/2+N/4+..)< N*log2N
可见,比较次数介于(N/2)log2N与Nlog2N之间。如果用大O表示法,时间复杂度也为 O(Nlog2N)。
作者:冰河winner
链接:https://www.jianshu.com/p/4e286f27b3df
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。