TSP(Hill Climbing、SA、GA)
What is TSP?
Scene: A traveling businessman called blank needs to visit n cities.
Conditions: blank need to choose a path to visit all the cities, but he can only visit each city once, and eventually returns to the starting point.
Goal: Find a smallest path.
I have learned the problem in Discrete Mathematics, which equals to finding the shortest Hamilton loop problem of graphs. In the book, it use Branch and Bound(分支定界法) to solve this problem. In this article, I am going to use three algorithms including Hill Climbing(爬山算法)、Simulated Annealing(模拟退火算法)、Genetic Algorithm(遗传算法) to solve this problem.
TSP Data
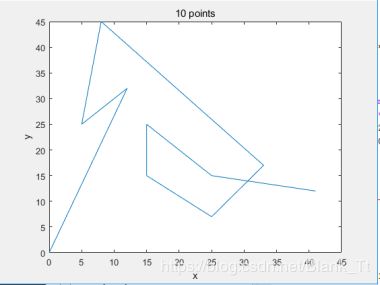
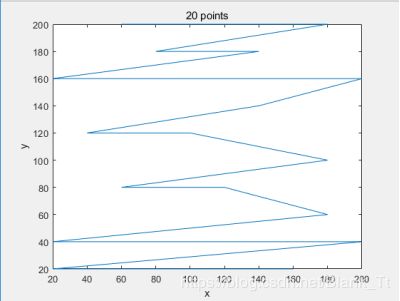
Select 10、20、30 data points respectively.
Graph1 city data1
Graph2 city data2
Graph3 city data3
Hill Climbing
Algorithm description
Starting with the current node, the values of the neighboring nodes are compared. If the current node is the largest, then return to the current node as the maximum (the peak of the mountain); On the contrary, replace the current node with the highest one, so as to achieve the purpose of climbing to the peak. The cycle lasts until it reaches its peak.
Main function
public Path findShortestPath(Path currentPath) { //find the shortest path
Path adjacentPath;
int count = 0;
String compareRoutes = null;
while(count < MAXMUM) {
adjacentPath = swapCities(new Path(currentPath));
if(adjacentPath.getTotalDistance() <= currentPath.getTotalDistance()) {
compareRoutes = " update";
count = 0;
currentPath = new Path(adjacentPath);
} else {
compareRoutes = " keep , iterative number:" + count;
count++;
}
System.out.println(" | " + compareRoutes);
System.out.print(currentPath + " | " + currentPath.getTotalStringDistance());
}
System.out.println(" | Possible Optimal Solution");
return currentPath;
}
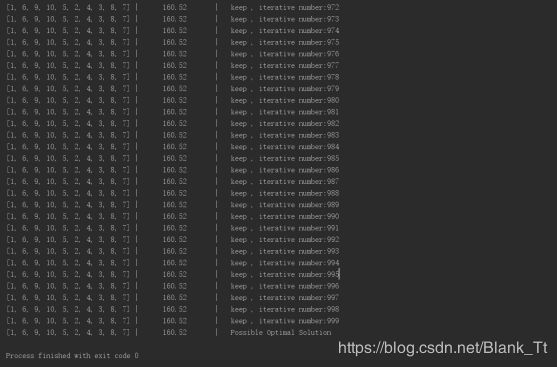
Result
Use 10 points to test.(Same below).The iteration number is 1000, and it seems the path(1 6 9 10 5 2 4 3 8 7) may be the optimal one.
Graph4 result of Hill Climbing
Simulated Annealing
Algorithm description
In order to overcome the disadvantage that local search algorithm is easy to fall into local optimal solution, SA uses probability-based two-direction random search technology: when a neighborhood-based operation improves the quality of the current solution, simulated annealing algorithm accepts the improved solution as a new current solution; in the opposite case, it calculates. The method takes a certain probability exp(-ΔC/T) as the new current solution, in which ΔC is the difference of the evaluation value of the solution before and after neighborhood operation, and T is the control parameter (temperature) of annealing process. Simulated annealing algorithm has been proved theoretically to be a global optimization algorithm which converges to the global optimal solution with probability 1.
Main function
public void SA(){
init();
copyPath(initPath,bestPath);
bestDis = totalDis(initPath);
initDis = bestDis;
int k = 0; //iteration number
int n = 0; //step
float t = t0;
float r = 0.0f;
while(k < T){
n = 0;
while(n < len){
adjacent(initPath,tempPath);
tempDis = totalDis(tempPath);
if(tempDis < bestDis){
copyPath(tempPath,bestPath);
bestT = k;
bestDis = tempDis;
}
r = random.nextFloat();
if(tempDis< initDis || Math.exp((initDis- tempDis) / t) > r){
copyPath(tempPath, initPath);
initDis = tempDis;
}
n++;
}
t *= a;
k++;
}
System.out.println("Optimum T:");
System.out.println(bestT);
System.out.println("Optimum dis:");
System.out.println(bestDis);
System.out.println("Optimum path:");
for (int i = 0; i < cityNum; i++) {
System.out.print(bestPath[i] + ",");
if (i % 10 == 0 && i != 0) {
System.out.println();
}
}
}
Result
Graph5 result of SA
Genetic Algorithm
Algorithm description
General steps of genetic algorithm
1、Random Generated Population
2、According to the strategy, the fitness of the individual is judged whether it conforms to the optimization criterion or not. If it does, the best individual and its optimal solution are output, and the end is achieved. Otherwise, proceed to the next step.
3、Parents are selected according to their fitness. Individuals with high fitness are selected with high probability and those with low fitness are eliminated.
4、The parents' chromosomes are crossed in a certain way to produce offspring.
5、The chromosomes of offspring were mutated.
6、Generate a new generation of population by crossover and mutation, then return to step 2 until the optimal solution is generated
How to solve TSP with GA
Because every city has its own name(use index instead), I decide to use the index as the sequence of genes. The first thing I need to do is creating the initial population, then calculating species’ fitness to find the most talent one. This step needs to be performed for many times (DEVELOP_NUM ). Next, use“Roulette gambling”to choose. In the following, use probability pcl~pch to finish crossover. At last,use probability pm to mutate (change subscript).
Main function
SpeciesIndividual run(SpeciesPopulation list)
{
//create population
createBeginningSpecies(list);
for(int i=1;i<=TSPData.DEVELOP_NUM;i++)
{
select(list);
crossover(list);
mutation(list);
}
return getBest(list);
}
Select:
void select(SpeciesPopulation list)
{
//计算适应度
calRate(list);
//找出最大适应度物种
Double talentDis= Double.MAX_VALUE;
SpeciesIndividual talentSpecies=null;
SpeciesIndividual point=list.head.next;
while(point!=null)
{
if(talentDis > point.distance)
{
talentDis=point.distance;
talentSpecies=point;
}
point=point.next;
}
//copy the best one for talentNum;
SpeciesPopulation newSpeciesPopulation = new SpeciesPopulation();
int talentNum=(int)(list.speciesNum/4);
for(int i=1;i<=talentNum;i++)
{
SpeciesIndividual newSpecies=talentSpecies.clone();
newSpeciesPopulation.add(newSpecies);
}
//list.speciesNum-talentNum次
int roundNum=list.speciesNum-talentNum;
for(int i=1;i<=roundNum;i++)
{
//产生0-1的概率
double rate=(double) Math.random();
SpeciesIndividual oldPoint=list.head.next;
while(oldPoint != null && oldPoint != talentSpecies)
{
if(rate <= oldPoint.rate)
{
SpeciesIndividual newSpecies=oldPoint.clone();
newSpeciesPopulation.add(newSpecies);
break;
}
else
{
rate=rate-oldPoint.rate;
}
oldPoint=oldPoint.next;
}
if(oldPoint == null || oldPoint == talentSpecies)
{
//复制最后一个
point=list.head;//游标
while(point.next != null)//寻找表尾结点
point=point.next;
SpeciesIndividual newSpecies=point.clone();
newSpeciesPopulation.add(newSpecies);
}
}
list.head = newSpeciesPopulation.head;
}
Crossover:
void crossover(SpeciesPopulation list)
{
//以概率pcl~pch进行
double rate=(double)Math.random();
if(rate > TSPData.pcl && rate < TSPData.pch)
{
SpeciesIndividual point=list.head.next;//游标
Random rand=new Random();
int find=rand.nextInt(list.speciesNum);
while(point != null && find != 0)//寻找表尾结点
{
point=point.next;
find--;
}
if(point.next != null)
{
int begin=rand.nextInt(TSPData.CITY_NUM);
//取point和point.next进行交叉,形成新的两个染色体
for(int i=begin;i
Mutation:
void mutation(SpeciesPopulation list)
{
SpeciesIndividual point=list.head.next;
while(point != null)
{
float rate=(float)Math.random();
if(rate < TSPData.pm)
{
Random rand=new Random();
int left=rand.nextInt(TSPData.CITY_NUM);
int right=rand.nextInt(TSPData.CITY_NUM);
if(left > right)
{
int tmp;
tmp=left;
left=right;
right=tmp;
}
//逆转left-right下标元素
while(left < right)
{
int tmp;
tmp=point.genes[left];
point.genes[left]=point.genes[right];
point.genes[right]=tmp;
left++;
right--;
}
}
point=point.next;
}
}
Result
Graph6 result of GA
Code:
SA:链接:https://pan.baidu.com/s/1R73OCwhPs3NA2DntgJkjqg
提取码:a6xa
GA:链接:https://pan.baidu.com/s/1uE8qrzBdPei-GZwVxvwscA
提取码:pa7t
Hill Climbing链接:https://pan.baidu.com/s/1Rmq0qZgpHoEDV8txl03ukA
提取码:bstf