杭电多校第四场 1002 HDU-6333(组合数+莫队)
Problem B. Harvest of Apples
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1039 Accepted Submission(s): 390
Problem Description
There are n apples on a tree, numbered from 1 to n.
Count the number of ways to pick at most m apples.
Input
The first line of the input contains an integer T (1≤T≤105) denoting the number of test cases.
Each test case consists of one line with two integers n,m (1≤m≤n≤105).
Output
For each test case, print an integer representing the number of ways modulo 109+7.
Sample Input
2
5 2
1000 500
Sample Output
16
924129523
题目大意:给出n个苹果,问你至多拿走m个苹果的方案数是多少?
题目思路:由于苹果是相同的,所以最终的答案就是 不拿苹果的方案数+拿一个苹果的方案数+拿两个苹果的方案数+...+拿m个苹果的方案数。那么最终就是要求解: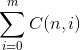 。
。
通过预处理之后,我们求解单个答案的复杂度就是O(m),但由于本题的T较大,这个复杂度是不合理的。
![]()
![]()
式子一很容易就能推出来,现在来证明下式子二。
由组合数公式我们知道![]()
那么
![]()
由于![]()
故![]() 。
。
我们得到这两个式子之后,我们就可以在O(1)的时间里由![]() 求出
求出![]() 。
。
这样我们就可以借助莫队来完成这个问题,对T进行离线操作,再通过移动左右指针来解决答案。
这题可以先预处理出阶乘和所有的阶乘的逆元,那么就可以借助![]() 在O(1)的时间内完成转移。
在O(1)的时间内完成转移。
这样整体的复杂度为![]() 。
。
具体实现看代码:
#include
#define fi first
#define se second
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define pb push_back
#define MP make_pair
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=b;i>=a;i--)
#define FIN freopen("in.txt","r",stdin)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pairpii;
using namespace std;
const int MX=1e5+7;
const int mod=1e9+7;
struct Query{
int n,m,id;
}que[MX];
int pos[MX];
ll inv[MX],f[MX],ans[MX];
bool cmp(Query A,Query B){
if(pos[A.n]!=pos[B.n]) return A.n>=1;}return res;}
void init(){
f[1]=1;
for(int i=2;i n) return 0;
if(m == 0 || m == n) return 1;
return f[n]*inv[n-m]%mod*inv[m]%mod;
}
ll res=1;
int main(){
init();
int T;scanf("%d",&T);
int block=(int)sqrt(MX);
rep(i,1,MX-1) pos[i]=(i-1)/block;
rep(i,1,T){
scanf("%d%d",&que[i].n,&que[i].m);
que[i].id=i;
}
sort(que+1,que+T+1,cmp);
int N=1,M=0;
rep(i,1,T){
while(Nque[i].n) res=((res+C(--N,M))*inv[2])%mod;
while(Mque[i].m) res=(res-C(N,M--)+mod)%mod;
ans[que[i].id]=res;
}
rep(i,1,T)
printf("%lld\n", ans[i]);
return 0;
}
