2020 Multi-University Training Contest 1

6754 Distinct Sub-palindromes

找规律 从长度为4开始的串就一样了

#include
using namespace std;
int main(void) {
	int T, n;
	scanf("%d", &T);
	while (T--) {
		scanf("%d", &n);
		if (n == 1)printf("26\n");
		else if (n == 2)printf("676\n");
		else if (n == 3)printf("17576\n");
		else printf("15600\n");
	}
	return 0;
}

6755 Fibonacci Sum

题解：https://blog.csdn.net/u014609452/article/details/53039223

#include
using namespace std;
typedef long long ll;
const ll p = 1e9 + 9;
const ll InvSqrt5 = 276601605;
const ll A = 691504013;//1+根号5 / 2
const ll InvA = 691504012;
const ll B = 308495997;//1-根号5 / 2
const ll InvB = 308495996;
const int maxk = 1e5 + 5;
ll pa[maxk], pb[maxk], inv[maxk], fac[maxk];
ll ksm(ll a, ll n) {
    ll ret = 1;
    while (n) {
        if (n & 1)ret = (ret * a) % p;
        a = (a * a) % p;
        n >>= 1;
    }
    return ret % p;
}
ll Cnm(int n, int m) {
    return fac[n] * inv[m] % p * inv[n - m] % p;
}
ll Inv(ll x) {
    return ksm(x, p - 2);
}
ll ans, N, C;
int T, K;
int main(void) {
    pa[0] = pb[0] = fac[0] = 1;
    for (int i = 1; i < maxk; i++) fac[i] = fac[i - 1] * i % p;
    inv[1] = 1;
    for (int i = 2; i < maxk; i++) inv[i] = (p - p / i) * inv[p % i] % p;
    inv[0] = 1;
    for (int i = 1; i < maxk; i++) inv[i] = inv[i] * inv[i - 1] % p;
    for (int i = 1; i < maxk; i++) {
        pa[i] = pa[i - 1] * A % p;
        pb[i] = pb[i - 1] * B % p;
    }
    scanf("%d", &T);
    while (T--) {
        scanf("%lld %lld %d", &N, &C, &K);
        C = C % (p - 1);
        ll N2 = N % (p - 1);
        ll InvAC = ksm(InvA, C);
        ll BC = ksm(B, C);
        ans = 0;
        ll t = ksm(pa[K + 1] * InvB % p, C);
        for (ll r = 0; r <= K; r++) {
            t = t * BC % p * InvAC % p;
            ll tmp = t == 1 ? (N % p) : (t * (ksm(t, N2) - 1 + p) % p * Inv(t - 1) % p);
            tmp = Cnm(K, r) * tmp % p;
            if (r & 1)tmp = (p - tmp) % p;
            ans = (ans + tmp) % p;
        }
        ans = ans * ksm(InvSqrt5, K) % p;
        printf("%lld\n", ans);
    }
    return 0;
}

6759 Leading Robots

半平面交裸题+1

#include
#include
#include
#include
#include
#include
using namespace std;
const double INF = 1e12;
const double eps = 1e-8;
map<pair<double, double>, int>id;
bool no[50005];
int sgn(double x) {
    if (fabs(x) < eps)return 0;
    else return x < 0 ? -1 : 1;
}
struct Point {
    double x, y;
    Point() {}
    Point(double x, double y) :x(x), y(y) { }
    Point operator + (Point B) { return Point(x + B.x, y + B.y); }
    Point operator - (Point B) { return Point(x - B.x, y - B.y); }
    Point operator * (double k) { return Point(x * k, y * k); }
};
typedef Point Vector;
double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }//叉积
struct Line {
    Point p;
    Vector v;
    double ang;
    bool chong;
    Line() {}
    Line(Point p, Vector v, bool chong = false) :p(p), v(v), chong(chong) { ang = atan2(v.y, v.x); }
    bool operator < (Line& L) { return ang < L.ang; }
};
bool OnLeft(Line L, Point p) { return sgn(Cross(L.v, p - L.p)) > 0; }
Point Cross_Point(Line a, Line b) {
    Vector u = a.p - b.p;
    double t = Cross(b.v, u) / Cross(a.v, b.v);
    return a.p + a.v * t;
}
vector<Point>HPI(vector<Line>& L) {
    int n = L.size();
    sort(L.begin(), L.end());
    int first, last;
    vector<Point>p(n);
    vector<Line>q(n);
    vector<Point>ans;
    q[first = last = 0] = L[0];
    for (int i = 1; i < n; i++) {
        while (first < last && !OnLeft(L[i], p[last - 1])) {
            last--; no[last] = false;
        }
        while (first < last && !OnLeft(L[i], p[first]))first++;
        q[++last] = L[i];
        if (L[i].chong)no[last - 1] = true;//接下来的点会是重合点
        if (fabs(Cross(q[last].v, q[last - 1].v)) < eps) {
            last--;
            no[last] = false;
            if (OnLeft(q[last], L[i].p)) {//如果左边的直线是L[i]
                if (L[i].chong)no[last - 1] = true;
                q[last] = L[i];
            }
        }
        if (first < last)p[last - 1] = Cross_Point(q[last - 1], q[last]);
    }
    while (first < last && !OnLeft(q[first], p[last - 1])) {
        last--; no[last] = false;
    }
    if (last - first <= 1) {
        ans.resize(2);
        return ans;
    }
    p[last] = Cross_Point(q[last], q[first]);
    for (int i = first; i <= last; i++) {
        if (no[i])continue;
        ans.push_back(p[i]);
    }
    return ans;
}
int main(void) {
    int T, n;
    scanf("%d", &T);
    while (T--) {
        id.clear();
        memset(no, 0, sizeof(no));
        scanf("%d", &n);
        vector<Line>L;
        L.push_back(Line(Point(0, 0), Vector(0, -1)));
        L.push_back(Line(Point(0, INF), Vector(-1, 0)));
        while (n--) {
            double a, b;
            scanf("%lf%lf", &a, &b);
            pair<double, double>tmp(a, b);
            if (id.count(tmp)) {
                L[id[tmp]].chong = true;
                continue;
            }
            L.push_back(Line(Point(0, a), Vector(1, b)));
            id[tmp] = L.size() - 1;
        }
        vector<Point>ans = HPI(L);
        printf("%d\n", ans.size() - 2);
    }
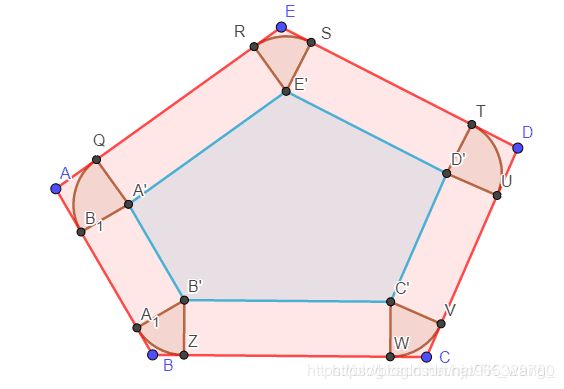
    return 0;
}

6762 Mow

看题意可以知道需要计算圆可以占据的最大面积
借用其它博文的图，由图可知面积为：小多边形的面积+周长*r+π*r^2
步骤：读入直线->直线向内平移r个单位长度->半平面交求点->计算多边形面积/周长

#include
#include
#include
#include
#include
const double pi = acos(-1);
const double eps = 1e-8;
using namespace std;
int sgn(double x) {
	if (fabs(x) < eps)return 0;
	else return x < 0 ? -1 : 1;
}
struct Point{
	double x, y;
	Point(){}
	Point(double x, double y) :x(x), y(y) {}
	Point operator + (Point B) { return Point(x + B.x, y + B.y); }
	Point operator - (Point B) { return Point(x - B.x, y - B.y); }
	Point operator * (double k) { return Point(x * k, y * k); }
	Point operator / (double k) { return Point(x / k, y / k); }
	Point turn90() { return Point(-y, x); }//逆时针转90度
	Point unit() { return Point(x / len(), y / len()); }
	double len() { return sqrt(x * x + y * y); }
};
typedef Point Vector;
inline double Dot(Vector A, Vector B) { return A.x * B.x + A.y * B.y; }
inline double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }
inline double pow2(double x) { return pow(x, 2); }
inline double dis(Point A, Point B) { return sqrt(pow2(A.x - B.x) + pow2(A.y - B.y)); }
struct Line{
	Point p;
	Vector v;
	double ang;
	Line(){}
	Line(Point p, Vector v) :p(p), v(v) { ang = atan2(v.y, v.x); }
	bool operator < (const Line& L) { return ang < L.ang; }
	void translation(double dis) {
		p = p + v.turn90().unit() * dis;
	}
};
inline bool OnLeft(Line L, Point p) { return sgn(Cross(L.v, p - L.p)) > 0; }
inline Point Cross_point(Line a, Line b) {
	Vector u = a.p - b.p;
	double t = Cross(b.v, u) / Cross(a.v, b.v);
	return a.p + a.v * t;
}
inline double Polygon_area(vector<Point>& p, int n) {
	double area = 0;
	for (int i = 0; i < n; i++)
		area += Cross(p[i], p[(i + 1) % n]);
	return area / 2;
}
vector<Point>HPI(vector<Line>L) {
	int n = L.size();
	sort(L.begin(), L.end());
	int first, last;
	vector<Point>p(n);
	vector<Line>q(n);
	vector<Point>ans;
	q[first = last = 0] = L[0];
	for (int i = 1; i < n; i++) {
		while (first < last && !OnLeft(L[i], p[last - 1]))last--;
		while (first < last && !OnLeft(L[i], p[first]))first++;
		q[++last] = L[i];
		if (fabs(Cross(q[last].v, q[last - 1].v)) < eps) {
			last--;
			if (OnLeft(q[last], L[i].p))q[last] = L[i];
		}
		if (first < last)p[last - 1] = Cross_point(q[last - 1], q[last]);
	}
	while (first < last && !OnLeft(q[first], p[last - 1]))last--;
	if (last - first <= 0)return ans;
	p[last] = Cross_point(q[last], q[first]);
	for (int i = first; i <= last; i++)ans.push_back(p[i]);
	return ans;
}
inline double perimeter(vector<Point>& p, int n) {
	double res = 0;
	for (int i = 0; i < n; i++)
		res += dis(p[i], p[(i + 1) % n]);
	return res;
}
const int N = 210;
int T, n, r, A, B;
vector<Point> p;
vector<Line> l;
int main(void) {
	//freopen("in.txt", "r", stdin);
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d%d%d", &n, &r, &A, &B);
		p.resize(n); l.resize(n);
		for (int i = 0; i < n; i++)
			scanf("%lf%lf", &p[i].x, &p[i].y);
		double area = Polygon_area(p, n);
		if (sgn(area) < 0) {//点可能是逆时针也可能是顺时针输入
			reverse(p.begin(), p.end());
			area *= -1;
		}
		double ans = area * A;
		if (A <= B) {
			printf("%.12f\n", ans);
			continue;
		}
		for (int i = 0; i < n; i++) {
			l[i] = Line(p[i], p[(i + 1) % n] - p[i]);
			l[i].translation(r);
		}
		p = HPI(l);
		double area2 = Polygon_area(p, p.size()) + perimeter(p, p.size()) * r + pi * r * r;
		if(p.size())ans = min(ans, fabs((area - area2) * A + area2 * B));
		printf("%.12f\n", ans);
	}
	return 0;
}