回溯法解决n皇后问题
1、算法描述:
回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树,当算法搜索至解空间树的某一节点时,先利用剪枝函数判断该节点是否可行(即能得到问题的解)。如果不可行,则跳过对该节点为根的子树的搜索,逐层向其祖先节点回溯;否则,进入该子树,继续按深度优先策略搜索。(说白了就是从一条路往前走,能进则进,不能进则退回来,换一条路再试。)
回溯法的基本行为是搜索,搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类:1. 使用约束函数,剪去不满足约束条件的路径;2.使用限界函数,剪去不能得到最优解的路径。
2、用回溯法解题的一般步骤:
(1)针对所给问题,确定问题的解空间:
首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
(2)确定结点的扩展搜索规则
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
3、算法框架
(1)问题框架
设问题的解是一个n维向量(a1,a2,………,an),约束条件是ai(i=1,2,3,…..,n)之间满足某种条件,记为f(ai)。
(2)非递归回溯框架
1:int a[n],i;
2: 初始化数组a[];
3: i = 1;
4: while (i>0(有路可走) and (未达到目标)) // 还未回溯到头
5: {
6: if(i > n) // 搜索到叶结点
7: {
8: 搜索到一个解,输出;
9: }
10: else // 处理第i个元素
11: {
12: a[i]第一个可能的值;
13: while(a[i]在不满足约束条件且在搜索空间内)
14: {
15: a[i]下一个可能的值;
16: }
17: if(a[i]在搜索空间内)
18: {
19: 标识占用的资源;
20: i = i+1; // 扩展下一个结点
21: }
22: else
23: {
24: 清理所占的状态空间; // 回溯
25: i = i –1;
26: }
27: }
(3)递归的算法框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单,其中i为搜索的深度,框架如下:
int a[n];
2: traceback(int i)
3: {
4: if(i>n)
5: 输出结果;
6: else
7: {
8: for(j = 下界; j <= 上界; j=j+1) // 枚举i所有可能的路径
9: {
10: if(fun(j)) // 满足限界函数和约束条件
11: {
12: a[i] = j;
13: ... // 其他操作
14: traceback(i+1);
15: 回溯前的清理工作(如a[i]置空值等);
16: }
17: }
18: }
19: }
4、n皇后问题
(1)问题描述: N皇后问题是一个经典的问题,在一个N*N的棋盘上放置N个皇后,每行一个并使其不能互相攻击(同一行、同一列、同一斜线上的皇后都会自动攻击)。
(2)问题分析:对于n皇后问题来说,其核心就是一个回溯问题,假设每个皇后都放在棋盘上的不同的行,则把这个条件就当成一个显示约束条件,后面则不用加以考虑位于不同行的问题,所以该问题的约束条件就简化成了两个皇后不能位于同一列和同一斜线,对于不位于同一列来说即两个皇后的纵坐标不想等即可满足这一条件,不位于同一斜线则两个皇后的连线的斜率不为1则满足该条件。
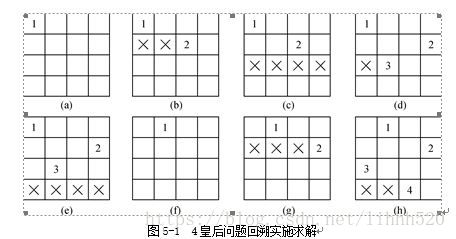
(3)问题实例:
如图所示是一个经典的四皇后求解问题
a.首先将第一个皇后放置于(1,1)。如图(a)
b.则对于第二个皇后来说,由于其不能与第一个皇后同列则不能放在(2,1)位置,又由于其不能与第一个皇后放在同一斜线上,则不能放在(2,2)位置(当位于(2,2)位置时,其与第一个皇后连线的斜率为1),则其可以放在(2,3)。(2,4),首先将其放在(2,3)
c对于第三个皇后来说,由于不能与第1,2个皇后同列,则不能在(3,1),(3,3),而又不能与第2个皇后同一斜线,则不能位于(3,2),(3,4)。则第3个皇后无处可放,则回溯到上一步,再次寻求合适的解。
d.即回溯到第2个皇后的位置,说明其放置在(2,3)无解,则放置到(2,4)这个位置,再依次考虑3,4皇后的位置问题。
e.....................
f.走完一次,可得到一个解为(1,1)(2,4)(3,1)(4,3)。
(4)C代码实现:
#include
#include
int n;
int x[50]={0};
int sum=0;
/**判断可不可以放置,
位于同一列
同一对角线则不能放置
**/
int Place(int k){
int i=1;
for(i=1;i
return 0;
}
return 1;
}
void Print()
{ int i;
printf("the location is:");
for ( i = 1; i <= n; ++i)
printf("(%d, %d) ", i, x[i]);
printf("\n");
}
void Traceback(int t){
int i;
if(t>n)
{
sum++;
Print();}
else
for(i=1;i<=n;i++)
{
x[t]=i;
if(Place(t))
Traceback(t+1);}
}
void Backtrack(){
int k=1;
while(k>0)
{
x[k]+=1;
while((x[k]<=n)&&!(Place(k)))
x[k]+=1;
if(x[k]<=n)
{ if(k==n)
{
sum++;
Print();
}
else
{
k++;
x[k]=0;//注意清0;
}
}
else
k--;
}
}
int main(){
printf("input the number of queens:");
scanf("%d",&n);
//Traceback(1);
Backtrack();
printf("There is %d methods",sum);
return 0;
}
reference:http://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741376.html