马尔可夫链蒙特卡罗法(Markov Chain Monte Carlo,MCMC)
文章目录
- 1. 蒙特卡罗法
- 2. 马尔可夫链
- 3. 马尔可夫链蒙特卡罗法
- 4. Metropolis-Hastings 算法
- 5. 吉布斯抽样
蒙特卡罗法(Monte Carlo method),也称为统计模拟方法(statistical simulation method),是通过从概率模型的随机抽样进行近似数值计算的方法
马尔可夫链蒙特卡罗法(Markov Chain Monte Carlo,MCMC),则是以马尔可夫链(Markov chain)为概率模型的蒙特卡罗法
马尔可夫链蒙特卡罗法 构建 一个马尔可夫链,使其平稳分布就是要进行抽样的分布,首先基于该马尔可夫链进行随机游走,产生样本的序列,之后使用该平稳分布的样本进行近似数值计算
马尔可夫链蒙特卡罗法被应用于概率分布的估计、定积分的近似计算、最优化问题的近似求解等问题,特别是被应用于统计学习中概率模型的学习与推理,是重要的统计学习计算方法
1. 蒙特卡罗法
- 核心思想:随机抽样(直接抽样法、接受-拒绝抽样法、重要性抽样法 等)
- 可用于数学期望估计、积分近似计算
- 一般的蒙特卡罗法中的
抽样样本是独立的,而马尔可夫链蒙特卡罗法中的抽样样本不是独立的,样本序列形成马尔科夫链。
2. 马尔可夫链
马尔可夫性:随机变量 X t X_t Xt 只依赖于前一个时刻 X t − 1 X_{t-1} Xt−1,不依赖于更早的时刻
齐次性:转移概率 P ( X t ∣ X t − 1 ) P(X_t|X_{t-1}) P(Xt∣Xt−1) 与 t t t 无关, P ( X t + s ∣ X t − 1 + s ) = P ( X t ∣ X t + 1 ) P(X_{t+s}|X_{t-1+s}) = P(X_t|X_{t+1}) P(Xt+s∣Xt−1+s)=P(Xt∣Xt+1)
马尔可夫链的状态分布由初始分布和转移概率分布决定 π ( t ) = P t π ( 0 ) \pi(t) = P^t \pi(0) π(t)=Ptπ(0)
马尔可夫链的平稳分布为 π ( π 1 , π 2 , . . . ) T \pi(\pi_1,\pi_2,...)^T π(π1,π2,...)T 的充要条件是: π \pi π 是下列方程组的解
x i = ∑ j p i j x j , i = 1 , 2 , . . . x i ≥ 0 , i = 1 , 2 , . . . ∑ i x i = 1 x_i = \sum\limits_j p_{ij}x_j, i = 1,2,...\\ x_i \ge 0, i=1,2,...\\ \sum\limits_i x_i = 1 xi=j∑pijxj,i=1,2,...xi≥0,i=1,2,...i∑xi=1
马尔可夫链可能存在唯一平稳分布,无穷多个平稳分布,或不存在平稳分布
性质:
-
不可约
P ( X t = i ∣ X 0 = j ) > 0 P(X_t=i|X_0=j)>0 P(Xt=i∣X0=j)>0 时刻0从状态 j 出发,时刻 t 到达状态 i 的概率大于 0,该链不可约
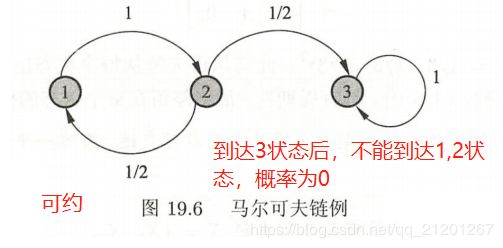
-
非周期
P ( X t = i ∣ X 0 = i ) > 0 P(X_t=i|X_0=i)>0 P(Xt=i∣X0=i)>0 时刻0从状态 i 出发,时刻 t 返回状态的所有时间长度的最大公约数是1,称该链是非周期的

定理:不可约且非周期的有限状态马尔可夫链,有唯一平稳分布存在 -
正常返
概率 p i j t p_{ij}^t pijt 为时刻 0 从状态 j 出发,时刻 t 首次转移到状态 i 的概率,若对所有状态 i, j,都满足 lim t → ∞ p i j t > 0 \lim\limits_{t\rightarrow \infty} p_{ij}^t >0 t→∞limpijt>0,称该链是正常返的
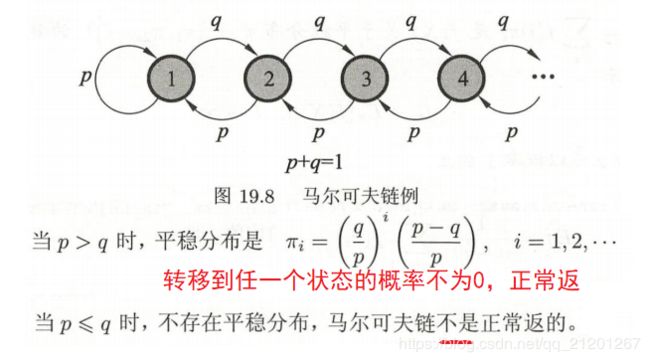
定理:不可约、非周期且正常返的马尔可夫链,有唯一平稳分布存在
- 可逆马尔可夫性
对任意状态 i,j,在任意时间 t 满足: p j i π j = p i j π i , i , j = 1 , 2 , . . . p_{ji}\pi_j = p_{ij}\pi_i, i,j=1,2,... pjiπj=pijπi,i,j=1,2,...(细致平衡方程)
如果有可逆的马尔可夫链,那么平稳分布作为初始分布,进行随机状态转移,无论是面向未来还是面向过去,任何一个时刻的状态分布都是该平稳分布。
定理:满足细致平衡方程的状态分布 π \pi π 就是该马尔可夫链的平稳分布
可逆马尔可夫链一定有唯一平稳分布,给出了一个马尔可夫链有平稳分布的充分条件(不是必要条件)
3. 马尔可夫链蒙特卡罗法
常用的马尔可夫链蒙特卡罗法 有Metropolis-Hastings算法、吉布斯抽样。
马尔可夫链蒙特卡罗法的收敛性的判断通常是经验性的
- 比如,在马尔可夫链上进行随机游走,检验遍历均值是否收敛
- 再比如,在马尔可夫链上并行进行多个随机游走,比较各个随机游走的遍历均值是否接近一致

