《信号与系统》5 连续信号与系统的复频域分析 MATLAB实现
连续信号与系统的复频域分析
- 参考与平台
- 简化拉普拉斯逆变换求解所用函数
- 求 H(s) = B(s) / A(s)的部分分式展开式函数 residue()
- 求取系统传递函数 tf ()
- 绘制 LTI 系统的零极点图 pzmap()
- 求取 LTI 系统单位阶跃响应函数 step()
- 求取 LTI 系统单位冲激响应函数 impulse()
- Example 1
- 问题
- 代码
- 结果
- Example 2
- 问题
- 结果
参考与平台
书籍《信号与系统》
matlab2016a
简化拉普拉斯逆变换求解所用函数
求 H(s) = B(s) / A(s)的部分分式展开式函数 residue()
用于求 H(s) = B(s) / A(s)的部分分式展开式。
命令 [r,p,k]=residue(num,den),
num 分子多项式 B(s)的系数,den 分母多项式 A(s)的系数
F(s)部分分式展开式中的留数 r、极点 p 和余项 k。
求取系统传递函数 tf ()
求取系统传递函数。
命令 sys = tf(num,den),
传递函数 sys 分子多项式系数 num,传递函数 sys 分母多项式系数 den
绘制 LTI 系统的零极点图 pzmap()
绘制 LTI 系统的零极点图。
命令 pzmap(sys)
求取 LTI 系统单位阶跃响应函数 step()
求取 LTI 系统单位阶跃响应。
命令 **step(sys)**或者 step(num,den)
求取 LTI 系统单位冲激响应函数 impulse()
求取 LTI 系统单位冲激响应。
命令 **impulse(sys)**或者 impulse(num,den)
Example 1
问题
MATLAB 实现部分分式展开
F ( s ) = s 2 + s + 2 s 3 + 5 s 2 + 6 s F(s)\;=\;\frac{s^2+s+2}{s^3+5s^2+6s} F(s)=s3+5s2+6ss2+s+2
代码
b =[1 1 2]; %分子多项式系数
a=[1 5 6 0]; %分母多项式系数
[r p k]=residue(b,a); %求出留数 r、极点 p 和余项 k
结果
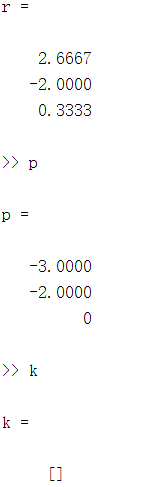
F(s)有 3 个极点,对应 3 个留数,无余项
H ( s ) = 2.6667 s + 3 + − 2 s + 2 + 0.3333 s H(s)\;=\;\frac{2.6667}{s+3}+\frac{-2}{s+2}+\frac{0.3333}s H(s)=s+32.6667+s+2−2+s0.3333
Example 2
问题
H (s)的零极点计算:
H ( s ) = s + 1 s 3 + 5 s 2 + 6 s H(s)\;=\;\frac{s+1}{s^3+5s^2+6s} H(s)=s3+5s2+6ss+1
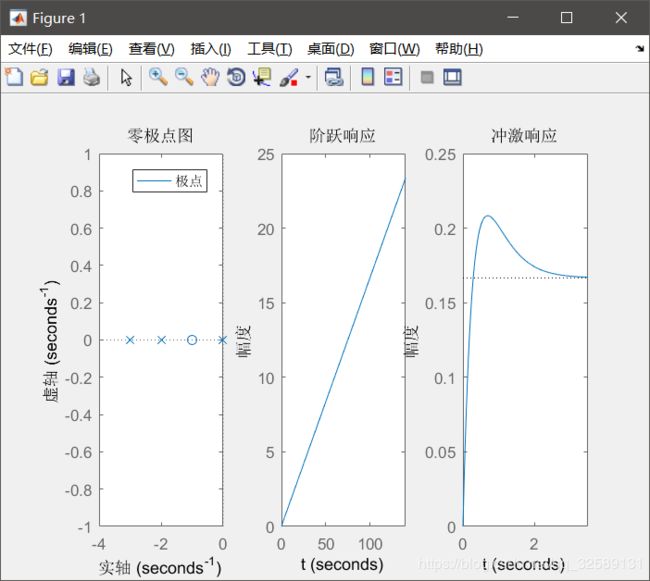
画出零极点图,并求阶跃响应 g(t)和冲激响应h(t)。
b=[1 1]; % 系统函数分子多项式系数
a=[1 5 6 0]; % 系统函数分母多项式系数
sys=tf(b,a); % 传递函数 H(s)
subplot(1,3,1),pzmap(sys); % 绘制零极点图
legend('极点','零点');
xlabel('实轴'),ylabel('虚轴');
title('零极点图');
subplot(1,3,2),step(b,a); % 阶跃响应 g(t)
xlabel('t'),ylabel('幅度');
title('阶跃响应');
subplot(1,3,3),impulse(b,a); % 冲激响应 h(t)
xlabel('t'),ylabel('幅度');
title('冲激响应');