Dijstra--讲解
这个算法只能计算单源最短路,而且不能计算负权值,这个算法是贪心的思想。
Dijkstra是按路径长度递增的顺序构造最短路径,每次都是从dist数组中选择最小的,然后加入已经确定出最短路的顶点的集合中,然后去更新,没有加入到已经确定出最短路的顶点的集合中,Dijkstra 每次循环都可以确定一个顶点的最短路径,故程序需要循环 n-1 次。
Dijkstra O(n^2) 单源最短路算法(计算从一个点到其他各点的最短路径),我们实际使用的dij使用优先队列优化的Dij时间复杂度为O(mlogn)。任何题目中都要注意的有四点事项:图是有向图还是无向图、是否有负权边,是否有重边,顶点到自身的可达性。
dist[i]表示源点到i点的最短路径.
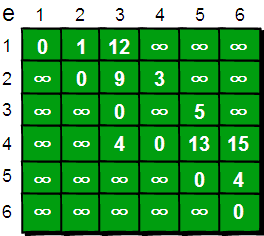
以为源点
1 2 3 4 5 6
dis 0 1 12 inf inf inf(一开始初始化dis源点,自己到自己0,不能直接到达的为inf,当然也可以,像下面一样初始化)
1 2 3 4 5 6
dis 0 inf inf inf inf inf
S存放已经找到的最短路径的节点,U存放没找到的
S={1},一开始只有源点
以第一种初始化方法为例:
从dist里面选一个最小的 是1,将其节点加入S,S={1,2},更新dist;
1 2 3 4 5 6
dis 0 1 10 4 inf inf
从dist里面选一个最小的 是4,将其节点加入S,S={1,2,4},更新dist;
1 2 3 4 5 6
dis 0 1 8 4 17 19
从dist里面选一个最小的 是8,将其节点加入S,S={1,2,4,3},更新dist;
1 2 3 4 5 6
dis 0 1 8 4 13 19
从dist里面选一个最小的 是13,将其节点加入S,S={1,2,4,3,5},更新dist;
1 2 3 4 5 6
dis 0 1 8 4 13 17
void Dijkstra(int s)
{
int vis[LEN] = {0};
for(int i=1; i<=n; i++)
dis[i] = INF;
dis[s] = 0;
for(int i=0; i
/*
使用优先队列Dijkstra算法
复杂度O(ElogE)
注意对vector E[MAXN]进行初始化后加边
*/
using namespace std;
const int INF=0x3f3f3f3f;
const int MAXN=1000010;
struct qnode
{
int v;
int c;
qnode(int _v=0,int _c=0):v(_v),c(_c){}
bool operator <(const qnode &r)const
{
return c>r.c;
}
};
struct Edge
{
int v,cost;
Edge(int _v=0,int _cost=0):v(_v),cost(_cost){}
};
vector E[MAXN];
bool vis[MAXN];
int dist[MAXN];
void Dijkstra(int n,int start)//点的编号从1开始
{
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;i++) dist[i]=INF;
priority_queue que;
while(!que.empty()) que.pop();
dist[start]=0;
que.push(qnode(start,0));
qnode tmp;
while(!que.empty())
{
tmp=que.top();
que.pop();
int u=tmp.v;
if(vis[u]) continue;
vis[u]=true;
for(int i=0;idist[u]+cost)
{
dist[v]=dist[u]+cost;
que.push(qnode(v,dist[v]));
}
}
}
}
void addedge(int u,int v,int w)
{
E[u].push_back(Edge(v,w));
}
int main()
{
for(int i=0;i<=MAXN;i++)
if(!E[i].empty())
E[i].clear();
// freopen("in.txt","r",stdin);
int n;
cin>>n;
int e;
cin>>e;
int u,v,w;
for(int i=1;i<=e;i++)
{
cin>>u>>v>>w;
addedge(u,v,w);
}
Dijkstra(n,1);
for(int i=1;i<=n;i++)
cout<