2019 HDU 多校二
1002 Beauty Of Unimodal Sequence
LIS+贪心:
up[i][0] 表示以 i 结尾的最长严格上升序列的最长长度;
up[i][1] 表示以 i 结尾的单峰最长的最长长度;
down[i][0] 表示以 i 开头的最长严格下降序列的最长长度;
down[i][1] 表示以 i 开头的单峰最长的最长长度;
上面的四个数组我们可以用线段树很容易就可以维护出来,然后我们可以通过遍历确定出最长单峰的长度。
就剩下如何去解决序列字典序最小和序列字典序最大
字典序最小很容易维护,直接贪心的去维护,如果当前位置可以构成单峰的一部分,那我们可以把这个位置放入答案
字典序最大如何维护?我看网上大佬的代码就是,直接反向求一遍字典序最小,反过来就是字典序最大?
感觉有道理,又找不到反例。。。。就当这个对的
参考博客:https://blog.csdn.net/Ratina/article/details/97273618#commentBox
代码:
#include
using namespace std;
const int maxn = 3e5 + 5;
int n, num[maxn], ranks[maxn], d;
int dp[maxn << 2];
int up[maxn][2], down[maxn][2];
int ans[maxn];
void clearTree(int sign, int l, int r) {
dp[sign] = 0;
if (l == r) return;
int mid = (l + r) >> 1;
clearTree(sign << 1, l, mid);
clearTree(sign << 1 | 1, mid + 1, r);
}
void pushup(int x) {
dp[x] = max(dp[x << 1], dp[x << 1 | 1]);
}
void update(int sign, int l, int r, int s, int x) {
if (l == r) {
dp[sign] = max(dp[sign], x);
return;
}
int mid = (l + r) >> 1;
if (s <= mid) update(sign << 1, l, mid, s, x);
else update(sign << 1 | 1, mid + 1, r, s, x);
pushup(sign);
}
int find(int sign, int l, int r, int a, int b) {
if (a > b) return 0;
if (l == a && r == b) return dp[sign];
int mid = (l + r) >> 1;
if (b <= mid) return find(sign << 1, l, mid, a, b);
else if (a > mid) return find(sign << 1 | 1, mid + 1, r, a, b);
else return max(find(sign << 1, l, mid, a, mid), find(sign << 1 | 1, mid + 1, r, mid + 1, b));
}
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%d", &num[i]);
ranks[i] = num[i];
}
sort(ranks + 1, ranks + 1 + n);
d = unique(ranks + 1, ranks + 1 + n) - (ranks + 1);
for (int i = 1; i <= n; i++) num[i] = lower_bound(ranks + 1, ranks + 1 + d, num[i]) - ranks;
clearTree(1, 1, d);
for (int i = 1; i <= n; i++) {
up[i][0] = find(1, 1, d, 1, num[i] - 1) + 1;
update(1, 1, d, num[i], up[i][0]);
}
clearTree(1, 1, d);
for (int i = 1; i <= n; i++) {
up[i][1] = up[i][0];
up[i][1] = max(up[i][1], find(1, 1, d, num[i] + 1, d) + 1);
update(1, 1, d, num[i], up[i][1]);
}
clearTree(1, 1, d);
for (int i = n; i >= 1; i--) {
down[i][0] = find(1, 1, d, 1, num[i] - 1) + 1;
update(1, 1, d, num[i], down[i][0]);
}
clearTree(1, 1, d);
for (int i = n; i >= 1; i--) {
down[i][1] = down[i][0];
down[i][1] = max(down[i][1], find(1, 1, d, num[i] + 1, d) + 1);
update(1, 1, d, num[i], down[i][1]);
}
int res = 0;
for (int i = 1; i <= n; i++) res = max(res, up[i][0] + down[i][0] - 1);
int cnt = 0, pre = 0;
for (int i = 1; i <= n; i++) {
if (num[i] > pre && cnt + down[i][1] == res) {
ans[++cnt] = i;
pre = num[i];
}
if (num[i] < pre && down[i][0] + cnt == res) {
ans[++cnt] = i;
pre = num[i];
}
}
for (int i = 1; i <= cnt; i++) {
printf("%d", ans[i]);
printf(i == cnt ? "\n" : " ");
}
cnt = pre = 0;
for (int i = n; i >= 1; i--) {
if (num[i] > pre && cnt + up[i][1] == res) {
ans[++cnt] = i;
pre = num[i];
}
if (num[i] < pre && up[i][0] + cnt == res) {
ans[++cnt] = i;
pre = num[i];
}
}
for (int i = cnt; i >= 1; i--) {
printf("%d", ans[i]);
printf(i == 1 ? "\n" : " ");
}
}
return 0;
} 1005 Everything Is Generated In Equal Probability
期望DP:
我们设 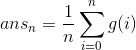 ,
,![]() 表示序列长度为 i 时的期望
表示序列长度为 i 时的期望![]() ,
,![]() 表示序列长度为 i 时逆序对的期望。
表示序列长度为 i 时逆序对的期望。![]()
我们将上面这个式子化简
我们可以预处理出![]() ,
,![]() ,
,![]() 。然后通过 O(n^2)来预处理
。然后通过 O(n^2)来预处理![]() ,顺便求出
,顺便求出![]() 的前缀和
的前缀和![]()
那么每次询问可以直接输出 ![]()
代码:
#include
using namespace std;
const int maxn = 3001;
typedef long long ll;
const ll mod = 998244353;
ll power(ll a, ll b, ll c) {
ll ans = 1;
while (b > 0) {
if (b & 1)
ans = ans * a % c;
a = a * a % c;
b >>= 1;
}
return ans;
}
ll n, c[maxn][maxn], p2[maxn], g[maxn], f[maxn], sum[maxn];
/// c 预处理组合数 p2 处理2^i f[i]=i*(i-1)/4
void init() {
ll inv = power(2, mod - 2, mod); ///2的逆元
p2[0] = 1;
for (ll i = 1; i < maxn; i++) {
c[i][0] = c[i][i] = 1;
p2[i] = p2[i - 1] * 2 % mod;
f[i] = (i * (i - 1) / 2LL) * inv % mod;
}
for (int j = 1; j < maxn; j++)
for (int i = j + 1; i < maxn; i++)
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
for (int i = 1; i < maxn; i++) {
ll temp = 0;
for (int j = 1; j <= i; j++)
temp = (temp + c[i][j] * g[i - j]) % mod;
temp = (temp + p2[i] * f[i]) % mod;
temp = temp * power((p2[i] - 1 + mod) % mod, mod - 2, mod) % mod;
g[i] = temp;
sum[i] = (sum[i - 1] + g[i]) % mod;
}
}
int main() {
init();
while (scanf("%lld", &n) != EOF)
printf("%lld\n", sum[n] * power(n, mod - 2, mod) % mod);
} 1008 Harmonious Army
网络流:
大佬说网络流做多了这道题就会了。。。
这是一个最小割+构图,要将图中的点分为两类点(战士和法师),相当于求最小割,最小割是求最小,然而答案要求最大,我们用权值和减去最小割不就得到最大值了嘛,但是要如何建图呢?
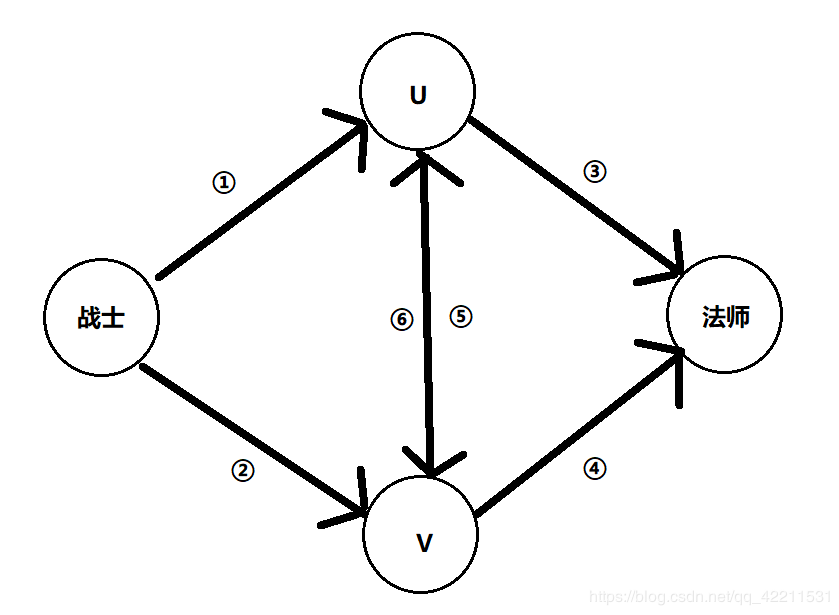
我们把源点当作战士阵营,汇点当作法师阵营。
如果我们将 u,v 划分为法师,那么 u,v 属于法师阵营,我们需要割掉的边就是①和②。
我们可以得到 ①+②=a+b=5a/4+c/3 ,①=②=5a/8+c/6
同理如果我们将 u,v划分为战士,那么 u,v属于战士阵营,我们需要割掉的边就是③和④。
③+④=b+c=a/4+4c/3,③=④=a/8+2c/3
如果将u,v划分为两个阵营,有两个割边的方法
②+③+⑤=①+④+⑥=a+c,由上面的结果我们可以计算出⑤=⑥=a/4+c/6
边权我们搞定了,但是还有需要注意的一点a是4的倍数,c是3的倍数,但是我们上面出现的边权存在a/8和c/6,我们需要将边权扩大一倍再去跑最大流,最后答案再除2即可。
代码:
#include
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 1e5 + 5;
int n, m, Sta, End, depth[maxn];
/// S 源点(战士),E 汇点(法师)
struct node {
int e, c, p;
} load[maxn << 1];
int head[maxn], cur[maxn], sign;
void add_edge(int s, int e, int c) {
load[++sign] = node{e, c, head[s]};
head[s] = sign;
}
bool bfs() {
for (int i = 0; i <= End; i++)
depth[i] = -1;
depth[Sta] = 1;
queue q;
q.push(Sta);
while (!q.empty()) {
int s = q.front();
q.pop();
for (int i = head[s], e; ~i; i = load[i].p) {
e = load[i].e;
if (load[i].c > 0 && depth[e] == -1) {
depth[e] = depth[s] + 1;
q.push(e);
}
}
}
return depth[End] != -1;
}
int dfs(int s, int cost) {
if (s == End)
return cost;
for (int &i = cur[s], e; ~i; i = load[i].p) {
e = load[i].e;
if (depth[e] == depth[s] + 1 && load[i].c != 0) {
int c = dfs(e, min(cost, load[i].c));
if (c > 0) {
load[i].c -= c;
load[i ^ 1].c += c;
return c;
}
}
}
return 0;
}
void init() {
Sta = 0, End = n * 2 + 1;
sign = -1;
memset(head, -1, sizeof(head));
}
int main() {
while (scanf("%d %d", &n, &m) != EOF) {
init();
int s, e, a, b, c;
ll temp, ans = 0, all = 0;
while (m--) {
scanf("%d %d %d %d %d", &s, &e, &a, &b, &c);
all += (a + b + c) * 2;
add_edge(Sta, s, 5 * a / 4 + c / 3);
add_edge(s, Sta, 0);
add_edge(Sta, e, 5 * a / 4 + c / 3);
add_edge(e, Sta, 0);
///同为战士建边
add_edge(s, End, a / 4 + 4 * c / 3);
add_edge(End, s, 0);
add_edge(e, End, a / 4 + 4 * c / 3);
add_edge(End, e, 0);
///同为法师建边
add_edge(s, e, a / 2 + c / 3);
//add_edge(e, s, 0);
add_edge(e, s, a / 2 + c / 3);
//add_edge(s, e, 0);
///一战一法建边
}
while (bfs()) {
for (int i = 0; i <= End; i++)
cur[i] = head[i];
while (temp = dfs(Sta, INF))
ans += temp;
}
printf("%lld\n", (all - ans) / 2);
}
return 0;
} 1009 I Love Palindrome String
队友的题解:https://blog.csdn.net/KXL5180/article/details/97167638?tdsourcetag=s_pctim_aiomsg
回文自动机+哈希:
这道题很明显我们需要判断回文串的一半是否也是回文串,回文自动机可以求出本质的回文串,我们只需要再记录一个这个回文串出现的位置,最后利用哈希再判断这个回文串的一半是否也是回文串,哈希判断回文串:正着跑一遍哈希,逆着跑一遍哈希,最后判断区间哈希值是否相等。
代码:
#include
using namespace std;
typedef unsigned long long ull;
const ull hash1 = 402653189;
const int maxn = 3e5 + 5;
char s[maxn];
int ans[maxn], d;
ull hashpre[maxn], hashlast[maxn], p[maxn];
void get_hash() {
p[0] = 1;
hashpre[0] = hashlast[d + 1] = 0;
for(int i = 1; i <= d; i++)
p[i] = p[i - 1] * hash1;
for(int i = 1; i <= d; i++)
hashpre[i] = hashpre[i - 1] * hash1 + s[i];
for(int i = d; i >= 1; i--)
hashlast[i] = hashlast[i + 1] * hash1 + s[i];
}
ull get_pre(int l, int r) {
return hashpre[r] - hashpre[l - 1] * p[r - l + 1];
}
ull get_last(int l, int r) {
return hashlast[l] - hashlast[r + 1] * p[r - l + 1];
}
bool judge(int End, int len) {
///判断这个回文串的一半是不是也是回文串
int r = End;
int l = End - len + 1;
r = (l + r) >> 1;
len = (r - l + 1);
if(get_pre(l, l + len - 1) == get_last(r - len + 1, r))
return true;
return false;
}
struct PAM {
int last;
///d为建立回文自动机的字符串长度
///last上一次插入字符串停在的节点
struct Node {
int cnt, len, fail, child[27], pos;
Node(int len, int fail): len(len), fail(fail), cnt(0) {
memset(child, 0, sizeof(child));
};
};
vectorst;
inline int newnode(int len, int fail = 0) {
///新建一个点
st.emplace_back(len, fail);
return st.size() - 1;
}
inline int getfail(int x, int n) {
///x为当前点的编号,n为插入字符的位置
while(s[n] != s[n - st[x].len - 1])
x = st[x].fail;
return x;
}
inline void Insert(int i) {
int c = s[i] - 'a';
int cur = getfail(last, i);
///不存在这条边,新增节点
if(!st[cur].child[c]) {
int p = newnode(st[cur].len + 2, st[getfail(st[cur].fail, i)].child[c]);
st[cur].child[c] = p;
}
///更新last,数量+1
st[last = st[cur].child[c]].cnt++;
st[last].pos = i; ///记录这中类型回文串的出现的末尾
}
void init(char *s) {
st.clear();
d = strlen(s + 1);
s[0] = 0;
///偶串的根为0,奇串的根为1
///建立偶串和奇串的根和fail
/// 偶的fail->奇
newnode(0, 1), newnode(-1);
last = 0;
for(int i = 1; i <= d; i++) {
Insert(i);
ans[i] = 0;
}
}
void get_all() {
for(int i = st.size() - 1; i >= 0; i--)
st[st[i].fail].cnt += st[i].cnt;
}
void get_ans() {
for(int i = 2; i < st.size(); i++) {
///cout << st[i].pos << ' ' << st[i].len << endl;
if(judge(st[i].pos, st[i].len))
ans[st[i].len] += st[i].cnt;
}
}
} pam;
int main() {
while(~scanf("%s", s + 1)) {
pam.init(s);
pam.get_all();
get_hash();
pam.get_ans();
for(int i = 1; i <= d; i++) {
printf("%d", ans[i]);
printf(i == d ? "\n" : " ");
}
}
return 0;
} 1010 Just Skip The Problem
签到题:输出 n!即可
1011 Keen On Everything But Triangle
主席树:
询问一个区间能够构成三角形的最大边长,仔细想一下答案肯定是排序后相邻的三个数,这样才能满足周长最大,难道去暴力判断?不会T?肯定不会T!!!
加入我们一个区间的排好序,F[1]到F[n],如果我们暴力查找答案
如果F[n]=F[n-1]+F[n-2]不满足条件,继续找
如果F[n-1]=F[N-2]+F[N-3]不满足条件,继续找
我们会发现,如果一个区间一直不满条件,即找不到答案,那么这个区间的数满足斐波拉契数列,那么这个区间就被限制了大小,最多不会超过44。
我们直接用主席树模板去暴力判断即可。
代码:
#include
using namespace std;
const int maxn = 1e5 + 10;
typedef long long ll;
int n, q, num[maxn], ranks[maxn], d;
struct node {
int ls, rs, cnt;
} p[maxn * 40];
int root[maxn], times;
void insert(int &now, int old, int l, int r, int x) {
now = ++times;
p[now] = p[old], p[now].cnt++;
if (l == r) return;
int mid = (l + r) >> 1;
if (x <= mid) insert(p[now].ls, p[old].ls, l, mid, x);
else insert(p[now].rs, p[old].rs, mid + 1, r, x);
}
int find(int Sta, int End, int l, int r, int k) {
if (l == r) return l;
int mid = (l + r) >> 1, cnt = p[p[End].ls].cnt - p[p[Sta].ls].cnt;
if (k <= cnt) return find(p[Sta].ls, p[End].ls, l, mid, k);
else return find(p[Sta].rs, p[End].rs, mid + 1, r, k - cnt);
}
int main() {
while (scanf("%d %d", &n, &q) != EOF) {
int l, r;
times = root[0] = 0;
p[0] = node{0, 0, 0};
for (int i = 1; i <= n; i++) {
scanf("%d", &num[i]);
ranks[i] = num[i];
}
sort(ranks + 1, ranks + 1 + n);
d = unique(ranks + 1, ranks + 1 + n) - (ranks + 1);
for (int i = 1; i <= n; i++) {
int s = lower_bound(ranks + 1, ranks + 1 + d, num[i]) - ranks;
insert(root[i], root[i - 1], 1, d, s);
}
while (q--) {
scanf("%d %d", &l, &r);
int len = r - l + 1;
int k3 = len, k2 = len - 1, k1 = len - 2;
ll a, b, c, ans = -1;
while (k1 >= 1) {
a = find(root[l - 1], root[r], 1, d, k1);
b = find(root[l - 1], root[r], 1, d, k2);
c = find(root[l - 1], root[r], 1, d, k3);
a = ranks[a], b = ranks[b], c = ranks[c];
if (a + b > c) {
ans = a + b + c;
break;
} else
k3--, k2--, k1--;
}
printf("%lld\n", ans);
}
}
return 0;
} 1012 Longest Subarray
线段树+思维
#include
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int n, c, k, a[maxn];
int minn[maxn << 2], lazy[maxn << 2];
vector pos[maxn];
void build(int sign, int l, int r) {
minn[sign] = lazy[sign] = 0;
if (l == r)
return;
int mid = (l + r) >> 1;
build(sign << 1, l, mid);
build(sign << 1 | 1, mid + 1, r);
}
void pushup(int sign) {
minn[sign] = max(minn[sign << 1], minn[sign << 1 | 1]);
}
void pushdown(int sign) {
if (lazy[sign]) {
lazy[sign << 1] += lazy[sign], lazy[sign << 1 | 1] += lazy[sign];
minn[sign << 1] += lazy[sign], minn[sign << 1 | 1] += lazy[sign];
lazy[sign] = 0;
}
}
void update(int sign, int l, int r, int a, int b, int x) {
if (a > b)
return;
if (l == a && r == b) {
minn[sign] += x, lazy[sign] += x;
return;
}
pushdown(sign);
int mid = (l + r) >> 1;
if (b <= mid)
update(sign << 1, l, mid, a, b, x);
else if (a > mid)
update(sign << 1 | 1, mid + 1, r, a, b, x);
else {
update(sign << 1, l, mid, a, mid, x);
update(sign << 1 | 1, mid + 1, r, mid + 1, b, x);
}
pushup(sign);
}
int query(int sign, int l, int r) {
if(l == r)
return l;
if(minn[sign] != 1)
return 0;
pushdown(sign);
int mid = (l + r) >> 1;
if (minn[sign << 1] == 1)
return query(sign << 1, l, mid);
else if (minn[sign << 1 | 1] == 1)
return query(sign << 1 | 1, mid + 1, r);
return 0;
}
int main() {
while (~scanf("%d %d %d", &n, &c, &k)) {
int ans = 0;
build(1, 1, n);
for (int i = 1; i <= c; i++) {
pos[i].clear();
pos[i].push_back(0);
}
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
update(1, 1, n, pos[a[i]].back() + 1, i - 1, -1);
pos[a[i]].push_back(i);
int x = pos[a[i]].size() - k - 1;
if (x >= 0) {
int l = pos[a[i]][x] + 1, r = pos[a[i]][x + 1];
update(1, 1, n, l, r, 1);
}
int s = query(1, 1, n);
if (s)
ans = max(ans, i - s + 1);
}
printf("%d\n", ans);
}
return 0;
}