数据结构 课程设计报告 ：校园导航系统
完整代码及文档已上传https://download.csdn.net/download/qq_45772158/12615918
一 . 设计目的
随着高校的发展,校园面积不断扩大,校园内跨区域活动频繁,为了给校内师生和校外人士办公、教学、生活等方面带来更大的便利,以及面对校园信息化建设的全面推广和迅猛发展，本系统，将通过迪杰斯特拉和弗洛伊德算法，求出所需最短路径，进一步加强数字化校园建设。
二 . 设计内容和要求
图的最短路径问题是指从指定的某一点v开始，求得从该地点到图中其它各地点的最短路径。并且给出求得的最短路径的长度及途径的地点。
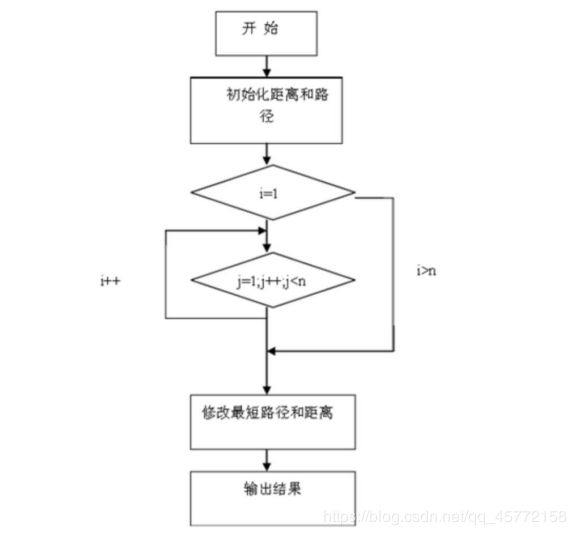
设计学校的平面图，至少包括10个以上的场所，每两个场所间可以有不同的路，且路长也可能不同，找出从任意场所到达另一场所最短路径（即用迪杰斯特拉算法），以及从任意场所到达所有场所的最短路径（即用弗洛伊德算法）。 功能要求：
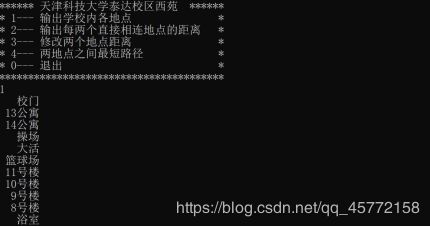
(1)输出顶点信息：将校园内各景点输出。
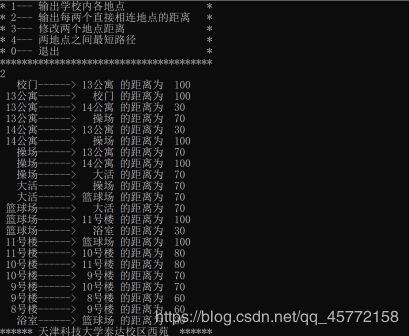
(2)输出边的信息：将校园内每两个位置（若两个位置之间有直接路径）的距离输出。
(3)修改：修改两个位置（若两个位置之间有直接路径）的距离，并重新输出每两个位置（若两个位置之间有直接路径）的距离；
(4)求最短路径：输出给定两点之间的最短路径的长度及途经的地点，输出任意一点与其他各点的最短路径。
三 . 校园导航系统模块图
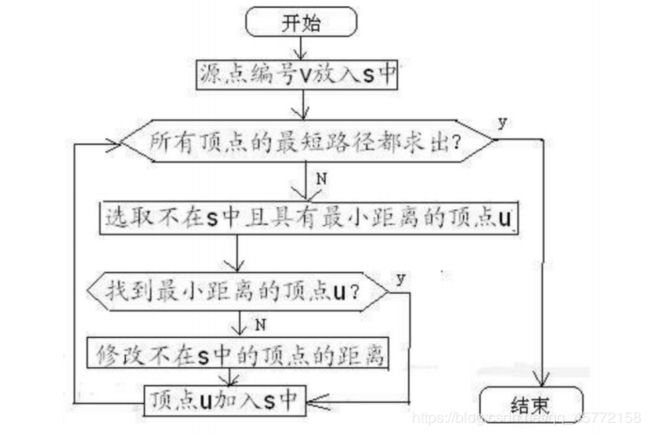
//迪杰斯特拉算法流程图
//弗洛伊德算法流程图
四、编码实现
1.结点结构体
typedef struct
{
char name[30]; //结点名称int num; //结点编号
}VEXTYPE;
typedef struct
{
VEXTYPE vexs[LENGTH];//结点value arcs[LENGTH][LENGTH];//弧
int vexnum,arcnum ;//结点数和最大路径
}MGraph;//邻接矩阵
2.输出学校内各地点
void PutOutVex(MGraph *G) // 功能 1 输出学校内各地点
{
for(int i=0;ivexnum;i++) cout
利用for循环，将数组中的数据输出
3.输出每两个直接相连地点的距离
void PutOutArc(MGraph *G) // 功能 2 输出每两个直接相连地点的距离
{
for(int i=0;ivexnum;i++)
for(int j=0;jvexnum;j++) if(G->arcs[i][j]
cout
}
利用两个for循环，将数据输出。利用MAX，可将不相邻顶点设置为距离无穷大 。
4.修改两个地址距离
void Change(MGraph *G) // 功能 3 修改：修改两个地址距离
{
int v0,v1,length;
cout<<" 修改：请输入起始顶点 :\n"; cin>>v0;
if(v0<0||v0>G->vexnum)
{
cout<<" 此点不存在 ! 请重新输入顶点 :"; cin>>v0;
}
cout<<" 请输入结束顶点 :\n"; cin>>v1;
if(v1<0||v1>G->vexnum)
{
cout<<" 此点不存在 ! 请重新输入顶点 :"; cin>>v1;
}
cout<<" 输入距离 :"; cin>>length;
G->arcs[v0][v1]=G->arcs[v1][v0]=length;
}
利用if语句，判断输入结点位置是否符合要求，同时保存两结点双向位置
5.使用 Dijkstra 算法求解最短路径
void Dijkstra(MGraph * G) // 功能 4. 求最短路径 输出两地点之间最短路径 使用 Dijkstra 算法求解最短路径
{
int v,w,i,min,t=0,x,v0,v1;
int final[20], D[20], p[20][20]; cout<<" 请输入起始顶点 :\n"; cin>>v0;
if(v0<0||v0>G->vexnum)
{
cout<<" 此点不存在 ! 请重新输入顶点 :"; cin>>v0;
}
cout<<" 请输入结束顶点 :\n"; cin>>v1;
if(v1<0||v1>G->vexnum)
{
cout<<" 此点不存在 ! 请重新输入顶点 :"; cin>>v1;
}
for(v=0;vvexnum;v++)
{
final[v]=0;
D[v]=G->arcs[v0][v]; for(w=0;wvexnum;w++) p[v][w]=0;
if(D[v]
p[v][v0]=1;p[v][v]=1;
}
}
D[v0]=0;final[v0]=1; for(i=1;ivexnum;i++)
{
min=MAX;
for(w=0;wvexnum;w++) if(!final[w]) if(D[w]
D[w]=min+G->arcs[v][w]; for(x=0;xvexnum;x++)
p[w][x]=p[v][x]; p[w][w]=1;
}
}
cout<<" 从 “
if(p[v1][j]==1)
cout
}
（1）初始化：先找处从源点V0到各终点V1的直达路径（V0,V1），即通过一条弧到达的路 径。
（2）选择：从这些路径中找出一条长度最短的路径（V0,x）。
（3）更新：然后对其余各条路径进行适当的调整：
若在图中存在弧（x,V1），且（x,V1）+（V0,x）<（V0,V1），则以路径（V0,x,V1）代替
（V0,V1）。
（4）在调整后的各条路径中，再找长度最短的路径，以此类推。
五、实验结果与分析
1.页面展示
2.输出学校内各地点
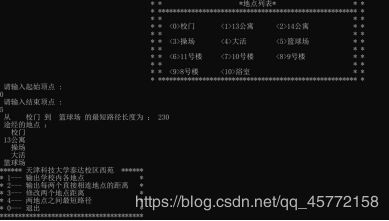
3.输出每两个直接相连地点的距离
4.修改两个地点距离
（当输入的顶点不符合要求时）
5.两地点之间最短路径
校门–>13公寓 20
13公寓–>操场 70
操场–>大活 70
大活–>篮球场 70 20+70*3=230
六、总结
本次课设对于我本人来说还是有些难度，编写过程遇到了很多问题，算法功能也有不足之处，尤其是在输出最短路径输出时总是输出空白。通过询问老师与同学，解决了这些问题。通过本次课程设 计，锻炼了自己的耐心，确实有些问题很难修改，但改出来很有成就感，希望后面加以总结，并继续学习下去。