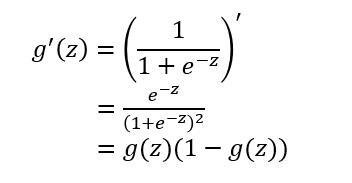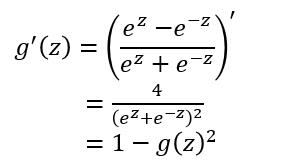神经网络中常用的几种激活函数的理解

1. 什么是激活函数

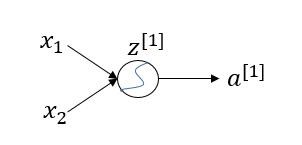
  在神经网络中，我们经常可以看到对于某一个隐藏层的节点，该节点的激活值计算一般分为两步：
  （1）输入该节点的值为 x1,x2x1,x2 时，在进入这个隐藏节点后，会先进行一个线性变换，计算出值 z[1]=w1x1+w2x2+b[1]=W[1]x+b[1]z[1]=w1x1+w2x2+b[1]=W[1]x+b[1] ，上标 11 表示第 11 层隐藏层。
  （2）再进行一个非线性变换，也就是经过非线性激活函数，计算出该节点的输出值(激活值) a(1)=g(z(1))a(1)=g(z(1)) ，其中 g(z)g(z) 为非线性函数。

 

---

2. 常用的激活函数

  在深度学习中，常用的激活函数主要有：sigmoid函数，tanh函数，ReLU函数。下面我们将一一介绍。

2.1 sigmoid函数

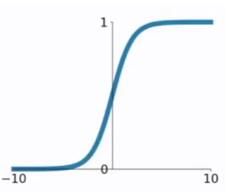
  在逻辑回归中我们介绍过sigmoid函数，该函数是将取值为 (−∞,+∞)(−∞,+∞) 的数映射到 (0,1)(0,1) 之间。sigmoid函数的公式以及图形如下：

 

g(z)=11+e−zg(z)=11+e−z

 

  对于sigmoid函数的求导推导为：

 

  sigmoid函数作为非线性激活函数，但是其并不被经常使用，它具有以下几个缺点：
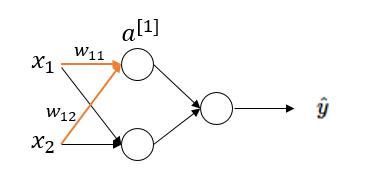
   （1）当 zz 值非常大或者非常小时，通过上图我们可以看到，sigmoid函数的导数 g′(z)g′(z) 将接近 00 。这会导致权重 WW 的梯度将接近 00 ，使得梯度更新十分缓慢，即梯度消失。下面我们举例来说明一下，假设我们使用如下一个只有一层隐藏层的简单网络：

 

   对于隐藏层第一个节点进行计算，假设该点实际值为 aa ，激活值为 a[1]a[1] 。于是在这个节点处的代价函数为（以一个样本为例）：

J[1](W)=12(a[1]−a)2J[1](W)=12(a[1]−a)2

   而激活值 a[1]a[1] 的计算过程为：

z[1]=w11x1+w12x2+b[1]z[1]=w11x1+w12x2+b[1]

 

a[1]=g(z[1])a[1]=g(z[1])

   于是对权重 w11w11 求梯度为：

ΔJ[1](W)Δw11=(a[1]−a)⋅(a[1])′=(a[1]−a)⋅g′(z[1])⋅x1ΔJ[1](W)Δw11=(a[1]−a)⋅(a[1])′=(a[1]−a)⋅g′(z[1])⋅x1

   由于 g′(z[1])=g(z[1])(1−g(z[1]))g′(z[1])=g(z[1])(1−g(z[1])) ，当 z[1]z[1] 非常大时，g(z[1])≈1，1−g(z[1])≈0g(z[1])≈1，1−g(z[1])≈0 因此， g′(z[1])≈0,ΔJ[1](W)Δw11≈0g′(z[1])≈0,ΔJ[1](W)Δw11≈0。当 z[1]z[1] 非常小时，g(z[1])≈0g(z[1])≈0 ，亦同理。（本文只从一个隐藏节点推导，读者可从网络的输出开始，利用反向传播推导）
   （2）函数的输出不是以0为均值，将不便于下层的计算，具体可参考引用1中的课程。
  sigmoid函数可用在网络最后一层，作为输出层进行二分类，尽量不要使用在隐藏层。
 

2.2 tanh函数

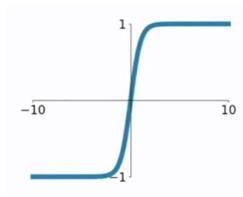
  tanh函数相较于sigmoid函数要常见一些，该函数是将取值为 (−∞,+∞)(−∞,+∞) 的数映射到 (−1,1)(−1,1) 之间，其公式与图形为：

 

g(z)=ez−e−zez+e−zg(z)=ez−e−zez+e−z

 

  tanh函数在 00 附近很短一段区域内可看做线性的。由于tanh函数均值为 00 ，因此弥补了sigmoid函数均值为 0.50.5 的缺点。
  对于tanh函数的求导推导为：

 

  tanh函数的缺点同sigmoid函数的第一个缺点一样，当 zz 很大或很小时，g′(z)g′(z) 接近于 00 ，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。
 

2.3 ReLU函数

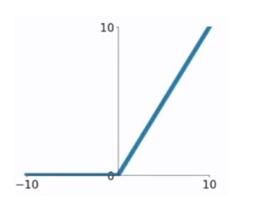
  ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。ReLU函数的公式以及图形如下：

 

g(z)={z,0,if z>0 if z<0g(z)={z,if z>0 0,if z<0

 

  对于ReLU函数的求导为：

 

g′(z)={1,0,if z>0 if z<0g′(z)={1,if z>0 0,if z<0

  ReLU函数的优点：
   （1）在输入为正数的时候（对于大多数输入 zz 空间来说），不存在梯度消失问题。
   （2） 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）
  ReLU函数的缺点：
   （1）当输入为负时，梯度为0，会产生梯度消失问题。
 

2.4 Leaky ReLU函数

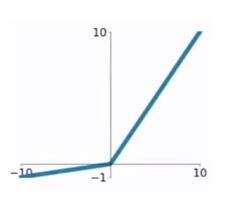
  这是一种对ReLU函数改进的函数，又称为PReLU函数，但其并不常用。其公式与图形如下：

 

g(z)={z,az,if z>0 if z<0g(z)={z,if z>0 az,if z<0

 

  其中 aa 取值在 (0,1)(0,1) 之间。
  Leaky ReLU函数的导数为：

 

g(z)={1,a,if z>0 if z<0g(z)={1,if z>0 a,if z<0

  Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题。

---

3. 为什么要用非线性激活函数？

  我们以这样一个例子进行理解。
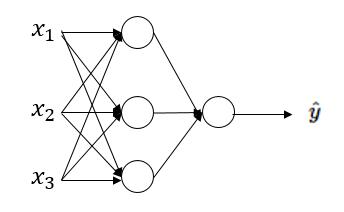
  假设下图中的隐藏层使用的为线性激活函数（恒等激活函数），也就是说 g(z)=zg(z)=z 。

 

  于是我们可以得出：

 

z[1]=W[1]x+b[1]z[1]=W[1]x+b[1]

 

a[1]=g(z[1])=z[1]a[1]=g(z[1])=z[1]

 

z[2]=W[2]a[1]+b[2]=W[2](W[1]x+b[1])+b[2]z[2]=W[2]a[1]+b[2]=W[2](W[1]x+b[1])+b[2]

 

a[2]=g(z[2])=z[2]=W[2](W[1]x+b[1])+b[2]=W[1]W[2]x+W[2]b[1]+b[2]a[2]=g(z[2])=z[2]=W[2](W[1]x+b[1])+b[2]=W[1]W[2]x+W[2]b[1]+b[2]

 

y^=a[2]=W[1]W[2]x+W[2]b[1]+b[2]y^=a[2]=W[1]W[2]x+W[2]b[1]+b[2]

  可以看出，当激活函数为线性激活函数时，输出 y^y^ 不过是输入特征 xx 的线性组合（无论多少层），而不使用神经网络也可以构建这样的线性组合。而当激活函数为非线性激活函数时，通过神经网络的不断加深，可以构建出各种有趣的函数。

---

引用及参考：
[1] https://mooc.study.163.com/learn/2001281002?tid=2001392029#/learn/content?type=detail&id=2001702017
[2] https://blog.csdn.net/kangyi411/article/details/78969642
[3] https://blog.csdn.net/cherrylvlei/article/details/53149381

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明