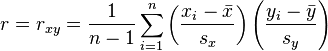序列的自相关和互相关计算
-- Ref [1] [2] [3] ------------------------------------------------------------------------
1.自相关和互相关概念
互相关(Cross-correlation)
对于连续函数,有如下定义:
对于离散函数,有如下定义:
在信号处理中,用互相关来衡量两个时间序列 x(t) 和 y(t) 在两个不同时刻 t1,t2 的取值之间的相似程度,通常可以用于在长序列中寻找一个特定的短序列。
在数理统计中,互相关用来两个随机序列的相关性。
从定义式中可以看到,互相关函数和卷积运算类似,也是两个序列滑动相乘,但是区别在于:
互相关的两个序列都不翻转,直接滑动相乘,求和;卷积的其中一个序列需要先翻转,然后滑动相乘,求和。
所以,f(t)和g(t) 做相关等于 f*(-t) 与 g(t) 做卷积。
自相关(Auto-correlation)
在信号分析当中通常将自相关函数称之为自协方差方程,定义如下:
自相关是互相关的一种特殊情况,就是一个序列和它本身做相关,主要用来衡量一个序列在不同时刻取值的相似程度。
在数理统计中,自相关的定义式如下:
如果随机过程是一个宽平稳过程,那么均值和方差都不是时间的函数,所以,自相关定义式变为:
在某些学科中,会去掉归一化因子σ2,使用自协方差来代替自相关。但是归一化因子可以让自相关的取值在 [-1, +1] 之间,不会随着序列的绝对大小而变化。
在信号处理中,
自相关的定义会去掉归一化,即不用减去均值,也不用除以方差。当除以方差时,一般叫做另外一个名字:自相关系数(Autocorrelation coefficient)。
2.相关(Correlation)
相关是概率论与统计学中用来刻画两个随机变量之间统计关系的强弱和方向的量。在广义的定义下,有很多种类的相关系数(Correlation coefficient),它们通常用字母ρ或者 r来表示。
我们通常说的相关系数的学名是:皮尔逊积差系数(Pearson's product moment coefficient),这种相关系数只对两个变量的线性关系敏感。
皮尔逊积差系数
Pearson 相关系数使用两个变量的协方差和标准差来定义:
其中,cov 是协方差,sigma 是标准差。因为 cov 可以写作:
![]()
所以 Person 相关系数的定义式可以写作:
根据概率论知识可以得到如下的变形形式:
基于样本来估计协方差和标准差,可以得到定义如下:
通过变形,可以得到下式:
-------------------------------------------------------------------------------------------
-- Ref [4] --------------------------------------------------------------------------------
3.MATLAB下计算相关的函数
具体函数描述和句式参看help,具体代码查看对应m文件,下面简述各函数输出:
xcorr
函数可输出两向量间的互相关(不等长补零)或者向量和矩阵的自相关,可返回时间延迟lags。
xcov
函数减去减去两序列的各自的均值后调用xcorr计算输出互协方差。
corrcoef
可计算多个序列的互相关和自相关,并依据自相关值归一化。序列表示为列向量,函数计算序列两两之间的皮尔逊互相关系数和自相关系数,自相关系数取值定为1进行归一化,返回延时为0时的相关系数取值(等同于 xcov(x,'coeff') 下0延时位置处的取值 )。可自行检验序列间是否相关,p<0.05。
autocorr
减去序列均值后计算自相关,并将0延时的取值定为1进行归一化并划分可信区间。
crosscorr
计算互相关系数(皮尔逊系数),并划分可信区间。
-------------------------------------------------------------------------------------------
参考链接:
[1]http://guqian110.github.io/pages/2015/03/16/correlation_coefficient_and_matlab_function.html
[2]http://blog.csdn.net/scuthanman/article/details/5588138
[3]http://blog.sina.com.cn/s/blog_6ce23c390101c6zc.html
[4]http://cn.mathworks.com/help/