TensorFlow实战（三）——基于LeNet-5模型实现MNIST手写数字识别

前言：

      本文将介绍一种经典的卷积神经网络的网络结构——LeNet-5模型，并给出一个完整的TensorFlow程序来实现LeNet-5模型。通过这个模型，我们可以得到卷积网络结构设计的一个通用模式。

一、卷积神经网络简介 

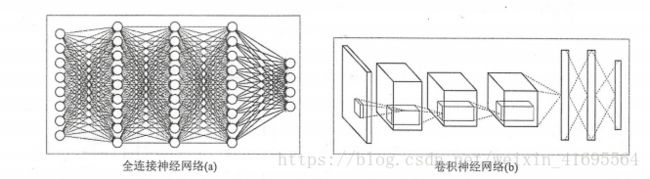
        在这一节中将讲解卷积神经网络与全连接神经网络（每两层之间的所有节点都是有边相连的）的差异，并介绍组成一 个卷积神经网络的基本网络结构。下图显示了全连接神经网络与卷积神经网络的结构对比图：

     从图中可以看出，卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样，卷积神经网络中的每一个节点都是一个神经元。在全连接神经网络中，每相邻两层之间的节点都有边相连，于是一般会将每一层全连接层中的节点组织成一列，这样方便显示连接结构。而对于卷积神经网络，相邻两层之间只有部分节点相连，为了展示每一层神经元的维度，一般会将每一层卷积层的节点组织成一个三维矩阵。  

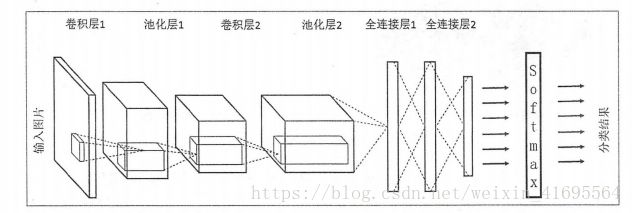
       除了结构相似，卷积神经网络的输入输出以及训练流程与全连接神经网络也基本一致。以图像分类为例，卷积神经网络的输入层就是图像的原始像素，而输出层中的每一个节点 代表了不同类别的可信度。这和全连接神经网络的输入输出是一致的。下图给出了一个更加具体的卷积神经网络架构图：

在卷积神经网络的前几层中，每一层的节点都被组织成一个三维矩阵。比如处理 Cifar-10数据集中的图片时，可以将输入层组织成一个32*32*3的三维矩阵。图中虚线部分展示了卷积神经网络的一个连接示意图，从图中可以看出卷积神经网络中前几层中每一个节点只和上一层中部分的节点相连。一个卷积神经网络主要由以下5种结构组成： 

       1.  输入层
       输入层是整个神经网络的输入，在处理图像的卷积神经网络中，它一般代表了一张图片的像素矩阵。比如在上图 中，最左侧的三维矩阵就可以代表一张图片。其中三维矩阵的长和宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道 (channel)。 比如黑白图片的深度为1，而在 RGB 色彩模式下，图像的深度为3。从输入层开始，卷积神经网络通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵，直到最后的全连接层。

       2.  卷积层
      从名字就可以看出，卷积层是一个卷积神经网络中最为重要的部分。和传统全连接层不同，卷积层中每一个节点的输入只是上一层神经网络的一小块，这个小块常 用的大小有 3 * 3或 者5 *5。卷积层试图将神经网络中的每一小块进行更加深入地分析从 而得到抽象程度更高的特征。一般来说，通过卷积层处理过的节点矩阵会变得更深，所以在上图中 可以看到经过卷积层之后的节 点矩阵的深度会增加。

       3. 池化层

       池化层神经网络不会改变三维矩阵的深度，但是它可以缩小矩阵的大小。池化操作可以认为是将一张分辨率较高的图片转化为分辨率较低的图片。通过池化层，可以进一步缩小最后全连接层中节点的个数，从而达到减少整个神经网络中参数的目的。
      4. 全连接层

       在经过多轮卷积层和池化层的处理之后，在卷积神经网络的最后一般会是由1到2个全连接层来给出最后的分类结果。经过几轮卷积层和池化层 的处理之后，可以认为图像中的信息己经被抽象成了信息含量更高的特征。我们可以将卷积层和池化层看成自动图像特征提取的过程。在特征提取完成之后，仍然需要使用全连接层来完成分类任务。
      5. Softmax层

       Softmax层主要用于分类问题。通过Softmax 层，可以得到当前样例属于不同种类的概率分布情况。

二、卷积神经网络常用结构

      接下来将详细介绍卷积神经网络中特殊的两个网络结构 ——卷积层和池化层。

      2.1 卷积层

       卷积层神经网络结构中最重要的部分，这个部分被称之为过滤器（filter）或者内核（kernel）。过滤器可以将当前层神经网络上的一个子节点矩阵转化为下一层神经网络上的一个单位节点矩阵。单位节点矩阵指的是一个长和宽都为   1，但深度不限的节点矩阵。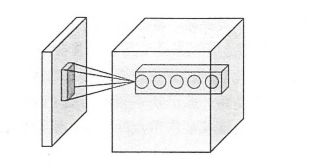

过滤器的尺寸指的是一个过滤器输入节点矩阵的大小，而深度指的是输出单位节点矩阵的深度。如上图所示，左侧小矩阵的尺寸为过滤器的尺寸，而右侧单位矩阵的深度为过滤器的深度。

过滤器的前向传播过程就是通过左侧小矩阵中的节点计算出右侧单位矩阵中节点的过程。

接下来通过一个具体的样例，来分析过滤器的前向传播过程。通过过滤器将一个2*2*3的节点矩阵变化为一个1*1*5的单位节点矩阵。假设使用来表示对于输出单位节点矩阵中的第个节点，过滤器输入节点的权重，使用表示第个输出节点对应的偏置项参数，那么单位矩阵中的第个节点的取值为：

其中为过滤器中节点的取值，为激活函数。

那么使用过滤器计算取值的过程为：

通过上面我们了解了在卷积层中计算一个过滤器的前向传播过程。卷积层结构的前向传播过程就是通过将一个过滤器从神经网络当前层的左上角移动到右下角，并且在移动中计算每一个对应的单位矩阵得到的。在这个过程中，首先将这个过 滤器用于左上角子矩阵，然后移动到左下角矩阵，再到右上角矩阵，最后到右下角矩阵。 过滤器每移动一次，可以计算得到一个值（当深度为k时会计算出k个值）。将这些数值拼接成一个新的矩阵，就完成了卷积层前向传播的过程。

当过滤器的大小不为1*1时，卷积层前向传播得到的矩阵的尺寸要小于当前层矩阵的尺寸，为了避免尺寸的变化，可以在当前层矩阵的边界上加入全0填充（zero-padding）。这样可以使得卷积层前向传播结果矩阵的大小和当前层矩阵保持一致。

下面的公式给出了在同时使用全0填充时结果矩阵的大小：

其中表示输出层矩阵的长度，它等于输入层矩阵长度除以长度方向上的步长的向上取整值；表示输出层矩阵的宽度，它等于输入层矩阵宽度除以宽度方向上的步长的向上取整值。

如果不使用全0填充，下面的公式给出了结果矩阵的大小：

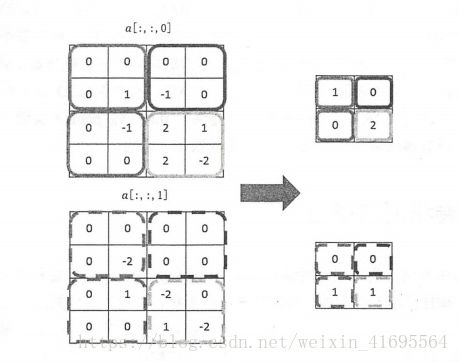
结合过滤器的使用方法，下图给出了使用了全0填充、步长为2的卷积层前向传播的计算流程：

下面的公式给出了左上角格子取值的计算方法，其他格 子可以依次类推：

2.2 池化层

在卷积层之间往往会加上一个池化层(pooling layer)o池化层可以非常有效地缩小矩阵的尺寸，从而减少最后全连接层中的参数。使用池化层既可以加快计算速度也有防止过拟合问题的作用。

与卷积层类似，池化层前向传播的过程也是通过移动一个类似过滤器的结构完成的。不过池化层过滤器中的计算不是节点的加权和，而是采用更加简单的最大值或者平均值运算。使用最大值操作的池化层被称之为最大池化层(max pooling)，这是被使用得最多的池化层结构。使用平均值操作的池化层被称之为平均池化层(average pooling)。

3*3*2节点矩阵经过全0填充且步长为2的最大池化层前向传播过程示意图如下：

下面的TensorFlow程序实现了最大池化层的前向传播算法：

# tf.nn.max_pool实现了最大池化层的前向传播过程，它的参数和tf .nn.conv2d函数类似。
# ksize提供了过滤器的尺寸，strides提供了步长信息，padding提供了是否使用全0填充。
pool = tf.nn.max_pool(input_max, ksize=[1, 3, 3, 1],strides=[1, 2, 2, 1], padding='SAME')

首先需要传入当前层的节点矩阵，这个矩阵是一个四维矩 阵，格式和tf.nn.conv2d函数中的第一个参数一致。第二个参数为过滤器的尺寸。虽然给出的是一个长度为4的一维数组，但是这个数组的第一个和最后一个数必须为1。这意味着池化层的过滤器是不可以跨不同输入样例或者节点矩阵深度的。在实际应用中使用得最多的池化层过滤器尺寸为[1,2,2,1]或者[1,3,3,1]。

tf.nn.max_pool函数的第三个参数为步长，它和tf.nn.conv2d函数中步长的意义是一样的，而且第一维和最后一维也只能为1。这意味着在TensorFlow中，池化层不能减少节点矩阵的深度或者输入样例的个数。tf.nn.max_pool函数的最后一个参数指定了是否使用全0填充。这个参数也只有两种取值——VALID或者SAME，其中VALID表示不使用全0填充，SAME表示使用全0填充。TensorFlow还提供了 tf.nn.avg_pool来实现平均池化层。tf.nn.avg_pool函数的调用格式和tf.nn.max_pool函数是一致的。

三、LeNet-5模型    

       LeNet-5模型是 Yann LeCun 教授于 1998年在论文 Gradient-based learning applied to document中提出的，它是第一个成功应用于数字识别问题的卷积神经网络。在MNIST数据集上，LeNet-5模型可以达到大约99.2%的正确率。LeNet-5模型总共有7层，下图展示了LeNet-5模型的架构：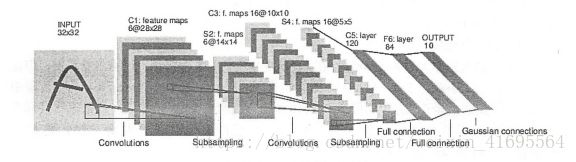

     接下来将介绍LeNet-5模型每一层的结构：

    （1）第一层：卷积层

      这一层的输入就是原始的图像像素，LeNet-5模型接受的输入层大小为32*32*1。第一个卷积层过滤器的尺寸为5*5，深度为6，不使用全0填充，步长为1。因为没有使用全0填充，所以这一层的输出的尺寸为32-5+1=28，深度为6。这一个卷积层总共有 5*5*1*6+6=156个参数，其中6个为偏置项参数。因为下一层的节点矩阵有28*28*6=4704个节点，每个节点和5*5=25个当前层节点相连，所以本层卷积层总共有4704 * (25+1)=122304连接。

    （2）第二层：池化层
      这一层的输入为第一层的输出，是一个28x28x6的节点矩阵。本层采用的过滤器大小为2x2，长和宽的步长均为2，所以本层的输出矩阵的大小为14*14*6。
    （3）第三层：卷积层
      本层的输入矩阵大小为14*14*6，使用的过滤器大小为5x5，深度为16。本层不使用全0填充，步长为1。本层的输出矩阵大小为10*10*16。按照标准的卷积层，本层应该有 5*5*6*16+16=2416个参数，10*10*16* (25+1) =41600个连接。

    （4）第四层：池化层
      本层的输入矩阵大小为 10 * 10 *1 6， 采用的过滤器大小为 2 x 2， 步长为2。本层的输出矩阵大小为5 * 5 * 16。
    （5）第五层：全连接层
     本层的输入矩阵大小为5 x 5 x 16，在 LeNet -5 模型的论文中将这一层称为卷积层，但是 因为过滤器的大小就是5 x 5，所以和全连接层没有区别，在之后的 TensorFlow 程序实现中 也会将这一层看成全连接层。 本层的输出节点个数为120，总共有  5 * 5 * 16 * 120+120=48120 个参数。
    （6）第六层：全连接层
      本层的输入节点个数为120个，输出节点个数为84个，总共参数为 120 * 84+84=10164  个。
    （7）第七层：全连接层

     本层的输入节点个数为84个，输出节点个数为10个，总共参数为84*10+10=850个。

四、代码演示 

上面介绍了LeNet-5模型每一层结构和设置，下面给出一个TensorFlow的程序来实现 一个类似LeNet-5模型的卷积神经网络来解决MNIST数字识别问题。通过TensorFlow训 练卷积神经网络的过程和训练全连接神经网络是完全一样的。唯一的区别在于因为卷积神经网络的输入层为一个三维矩阵，所以需要调整一下输入数据的格式。

mnist_inference.py文件中编写如下程序：

# -*- coding: utf-8 -*-

###################################
#########  作者：行歌   ############
#########  时间：2018.5.8  ########
######  email:[email protected]  ##
###################################

import tensorflow as tf

####定义神经网络结构相关的参数########
INPUT_NODE = 784         #输入层的节点数。对于MNIST数据集，这个就等于图片的像素
OUTPUT_NODE =10          #输出层的节点数。这个等于类别的数目。因为在MNIST数据集中
                         #需要区分的是0~9这10个数字，所以这里输出层的节点数为10

####定义与样本数据相关的参数########
IMAGE_SIZE =28            #像素尺寸
NUM_CHANNELS = 1          #通道数
NUM_LABELS = 10           #手写数字类别数目

#########第一层卷积层的尺寸和深度############
C0NV1_DEEP = 32
C0NV1_SIZE = 5
#########第二层卷积层的尺寸和深度############
CONV2_DEEP = 64
CONV2_SIZE = 5
##########全连接层的节点个数####################
FC_SIZE = 512


def inference(input_tensor, train, regularizer):
    """
    定义卷积神经网络的前向传播过程。这里添加了一个新的参数train，用于区分训练过程和测试过程。
    在这个程序中将用到dropout方法，dropout可以进一步提升模型可靠性并防止过拟合，dropout过程只在训练时使用。
    """

    # 声明第一层卷积层的变量并实现前向传播过程。
    # 通过使用不同的命名空间来隔离不同层的变量，这可以让每一层中的变量命名只需要考虑在当前层的作用，而不需要担心重名的问题。
    # 和标准LeNet-5模型不大一样，这里定义的卷积层输入为28x28x1的原始MNIST图片像素。
    # 因为卷积层中使用了全0填充，所以输出为28x28x32的矩阵。
    with tf.variable_scope('layer1-conv1'):
        conv1_weights = tf.get_variable("weight",
                                        [C0NV1_SIZE, C0NV1_SIZE, NUM_CHANNELS, C0NV1_DEEP],
                                        initializer=tf.truncated_normal_initializer(stddev=0.1))
        conv1_biases = tf.get_variable("bias", [C0NV1_DEEP], initializer=tf.constant_initializer(0.0))
        # 使用边长为5，深度为32的过滤器，过滤器移动的步长为1，且使用全0填充。
        conv1 = tf.nn.conv2d(input_tensor, conv1_weights, strides=[1, 1, 1, 1], padding='SAME')
        relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))

    # 实现第二层池化层的前向传播过程。这里选用最大池化层，池化层过滤器的边长为2，
    # 使用全0填充且移动的步长为2。这一层的输入是上一层的输出，也就是28x28x32 #的矩阵。输出为14x14x32的矩阵。
    with tf.name_scope("layer2-pool1"):
        pool1 = tf.nn.max_pool(relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

    # 声明第三层卷积层的变量并实现前向传播过程。这一层的输入为14x14x32的矩阵。输出为14x14x64的矩阵。
    # 通过tf.get_variable的方式创建过滤器的权重变量和偏置项变量。
    with tf.variable_scope("layer3-conv2"):
        conv2_weights = tf.get_variable("weight", [CONV2_SIZE,
                                                   CONV2_SIZE,
                                                   C0NV1_DEEP,
                                                   CONV2_DEEP],
                                                   initializer=tf.truncated_normal_initializer(stddev=0.1))
        # 卷积层的参数个数只与过滤器的尺寸、深度以及当前层节点矩阵的深度有关，所以这里声明的参数变
        # 量是一个四维矩阵，前面两个维度代表了过滤器的尺寸，第三个维度表示当前层的深度，第四个维度表示过滤器的深度。
        conv2_biases = tf.get_variable("bias", [CONV2_DEEP], initializer=tf.constant_initializer(0.0))

        conv2 = tf.nn.conv2d(pool1, conv2_weights, strides=[1, 1, 1, 1], padding='SAME')
        # 使用边长为5,深度为64的过滤器，过滤器移动的步长为1，且使用全0填充。
        # tf.nn.Conv2d提供了一个非常方便的函数来实现卷积层前向传播的算法。这个函数的第一个输入为当前层的节点矩阵。
        # 注意这个矩阵是一个四维矩阵，后面三个维度对应一个节点矩阵，第一维对应一个输入batch。
        # 比如在输入层，input [0,:，:,:]表示第一张图片，input [1,:，:,:]表示第二张图片，以此类推。
        # tf.rm.Conv2d第二个参数提供了卷积层的权重，第三个参数为不同维度上的步长。
        # 虽然第三个参数提供的是一个长度为4的数组，但是第一维和最后一维的数字要求一定是1。
        # 这是因为卷积层的步长只对矩阵的长和宽有效。最后一个参数是填充(padding)的方法，
        # TensorFlow中提供SAME或是VALID两种选择。其中SAME表示添加全0填充

        relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))
        # tf.nn.bias_add提供了一个方便的函数给每一个节点加上偏置项。注意这里不能直接使用加法，
        # 因为矩阵上不同位置上的节点都需要加上同样的偏置项。虽然下一层神经网络的大小为2*2,但是偏置项只有一个数(因为深度为1),
        # 而2*2矩阵中的每一个值都需要加上这个偏置项。


        # 实现第四层池化层的前向传播过程。这一层和第二层的结构是一样的。
        # 这一层的输入为14x14x64的矩阵，输出为7x7x64的矩阵。
        with tf.name_scope("layer4-pool2"):
            pool2 = tf.nn.max_pool(relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

            # 将第四层池化层的输出转化为第五层全连接层的输入格式。第四层的输出为7x7x64的矩阵，
            # 然而第五层全连接层需要的输入格式为向量，所以在这里需要将这个7x7x64的矩阵拉直成一
            # 个向量。 pool2.get_Shape函数可以得到第四层输出矩阵的维度而不需要手工计算。
            # 注意,因为每一层神经网络碎输入输出都为一个batch的矩阵，所以这里得到的维度也包含了一个batch中数据的个数。
            pool_shape = pool2.get_shape().as_list()

            # 计算将矩阵拉直成向量之后的长度，这个长度就是矩阵长宽及深度的乘积。
            # 注意这里pool_shape[0]为一个batch中数据的个数。
            nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]

            # 通过tf.reshape函数将第四层的输出变成一个batch的向量。
            reshaped = tf.reshape(pool2, [pool_shape[0], nodes])

            # 声明第五层全连接层的变量并实现前向传播过程。这一层的输入是拉直之后的一组向量，
            # 向量长度为3136，输出是一组长度为512的向量。此处引入了 dropout的概念。
            # dropout在训练时会随机将部分节点的输出改为0。dropout可以避免过拟合问题，从而使得模型在测试数据上的效果更好。
            # dropout一般只在全连接层而不是卷积层或者池化层使用。

        with tf.variable_scope("layer5-fc1"):
            fc1_weights = tf.get_variable("weight", [nodes, FC_SIZE],
                                          initializer=tf.truncated_normal_initializer(stddev=0.1))

            # 只有全连接层的权重需要加入正则
            # 当给出了正则化生成函数时，将当前变量的正则化损失加入名字为losses的集合。在这里
            # 使用了add_to_collection函数将一个张量加入一个集合，而这个集合的名称为losses。
            # 注意这是自定义的集合，不在TensorFlow自动管理的集合列表中。
            if regularizer != None:
                tf.add_to_collection('losses', regularizer(fc1_weights))
            fc1_biases = tf.get_variable('bias', [FC_SIZE], initializer=tf.constant_initializer(0.1))
            fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_biases)
            if train:
                fc1 = tf.nn.dropout(fc1, 0.5)

        # 声明第六层全连接层的变量并实现前向传播过程。这一层的输入为一组长度为512的向量，
        # 输出为一组长度为10的向量。这一层的输出通过Softmax之后就得到了最后的分类结果。
        with tf.variable_scope('layer6-fc2'):
            fc2_weights = tf.get_variable("weight", [FC_SIZE, NUM_LABELS],
                                          initializer=tf.truncated_normal_initializer(stddev=0.1))
            if regularizer != None:
                tf.add_to_collection('losses', regularizer(fc2_weights))
            fc2_biases = tf.get_variable("bias", [NUM_LABELS], initializer=tf.constant_initializer(0.1))
            logit = tf.matmul(fc1, fc2_weights) + fc2_biases

        # 返回第六层的输出。
        return logit

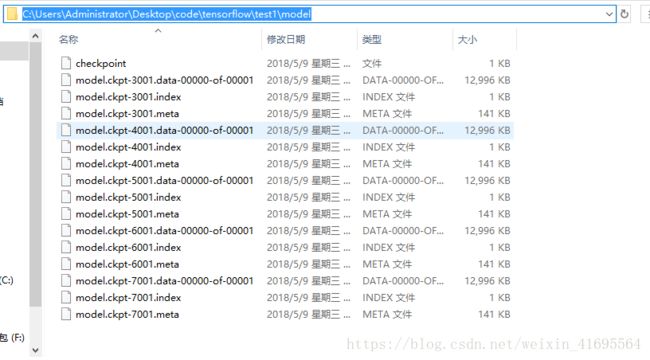
运行程序，最后得到LeNet-5模型，进入所在的文件夹，如下：

     接下来执行训练操作，在mnist_train.py文件中编写如下程序：

# -*- coding: utf-8 -*-

###################################
#########  作者：行歌   ############
#########  时间：2018.5.8  ########
######  email:[email protected]  ##
###################################

import tensorflow as tf
import numpy as np

from tensorflow.examples.tutorials.mnist import input_data

###加载mnist_inference.py中定义的常量和前向传播的函数########
import  mnist_inference

####配置实现指数衰减学习率的相关参数######
BATCH_SIZE = 100              #一个训练batch中的训练数据个数。数字越小时，训练过程越接近随机梯度下降；
                              #数字越大时，训练越接近梯度下降
LEARNING_RATE_BASE = 0.01      #基础的学习率
LEARNING_RATE_DECAY =0.99     #学习率的衰减系数

####配置实现正则化的相关参数######
REGULARAZTION_RATE = 0.0001      #正则化项的权重

####配置实现滑动平均模型的相关参数######
MOVING_AVERAGE_DECAY = 0.99     #滑动平均模型的衰减率

#############训练迭代轮数#########
TRAINING_STEPS = 8000

def train( mnist ):
    """
    定义输入输出placeholder，其中mnist_inference.INPUT_NODE为784，mnist_inference.OUTPUT_NODE为10。
    TensorFlow提供了tf.contrib.layers.l2_regularizer函数，它可以返回一个函数，
    这个函数可以计算一个给定参数的l2正则化项的值。类似的，
    tf.contrib.layers.l1_regularizer可以计算L1正则化项的值
    """
    # 调整输入数据placeholder的格式，输入为一个四维矩阵。第一维表示一个batch中样例的个数；
    # 第二维和第三维表示图片的尺寸；第四维表示图片的深度，对于RBG格式的图片，深度为5。
    x = tf.placeholder(tf.float32, [BATCH_SIZE,
                                    mnist_inference.IMAGE_SIZE,
                                    mnist_inference.IMAGE_SIZE,
                                    mnist_inference.NUM_CHANNELS], name = 'x-input1')

    y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE] , name='y-input')

    regularizer = tf.contrib.layers.l2_regularizer( REGULARAZTION_RATE )     #返回一个可以计算l2正则化项的函数

    y = mnist_inference.inference(x,True,regularizer)
    # 直接使用mnist_inference.py中定义的前向传播过程

    global_step = tf.Variable(0, trainable=False)
    # 定义存储训练轮数的变量，这个变量不需要计算滑动平均值，所以这里指定这个变量为不可训练的变量(trainable=False)。
    # 在使用tensorflow训练神经网络时，一般会将代表训练轮数的变量指定为不可训练的参数

    variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
    # 给定滑动平均衰减率和训练轮数的变量，初始化滑动平均类，ExponentialMovingAverage还提供了num_updates参数
    # 来动态设置decay的大小，因此，通过给定训练轮数的变量可以加快训练早期变量的更新速度

    variables_averages_op = variable_averages.apply( tf.trainable_variables())
    # 在所有代表神经网络参数的变量上使用滑动平均。其他辅助变量（比如global_step ）就不需要了。
    # tf.trainable_variables()返回的就是图上集合GraphKeys.TRAINABLE_VARIABLES中的元素。
    # 这个集合的元素就是所有没有指定trainable=False的参数

    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_,1))
    # 因为交叉熵一般会与softmax回归一起使用，所以TensorFlow对这两个功能进行了统一封装，
    # 并提供了tf.nn.softmax_cross_entropy_with_logits函数。比如：
    # cross_entropy = tf.nn.softmax_cross_entropy_with_logits（y,y_），其中y代表了原始神经网络的输出结果，而y_代表标准答案。
    # 这样通过一个命令就可以得到使用了softmax回归之后的交叉熵。在只有一个正确答案的分类问题中，TensorFlow还提供了
    # tf.nn.sparse_softmax_cross_entropy_with_logits函数来进一步加速计算过程。
    # 注意，tf.argmax(vector, axis=1)，其中axis：0表示按列，1表示按行。返回的是vector中的最大值的索引号，
    # 如果vector是一个向量，那就返回一个值，如果是一个矩阵，那就返回一个向量，
    # 这个向量的每一个元素都是相对应矩阵行的最大值元素的索引号。

    cross_entropy_mean = tf.reduce_mean(cross_entropy)
    loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
    # get_collection返回一个列表，这个列表包含所有这个losses集合中的元素，这些元素就是损失函数的不同部分，
    # 将它们加起来就可以得到最终的损失函数。
    # 其中tf.add_n([p1, p2, p3....])函数是实现一个列表的元素的相加。输入的对象是一个列表，列表里的元素可以是向量、矩阵等

    learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE,
                                               global_step,
                                               mnist.train.num_examples/BATCH_SIZE,
                                               LEARNING_RATE_DECAY,
                                               staircase=True)
    train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
    # 通过exponential_decay函数生成学习率，使用呈指数衰减的学习率，
    # 在minimize函数中传入global_step将自动更新global_step参数，从而使得学习率learning_rate也得到相应更新。

    with tf.control_dependencies([train_step, variables_averages_op]):
        train_op = tf.no_op(name='train')
    # 在训练神经网络模型时，每过一遍数据既需要通过反向传播来更新神经网络中的参数，
    # 又要更新每一个参数的滑动平均值。为了一次完成多个操作，TensorFlow提供了tf.control_dependencies机制

    saver = tf.train.Saver()
    # 初始化TensorFlow持久化类

    with tf.Session() as sess:
        # 初始化所有变量
        init_op = tf.global_variables_initializer()
        sess.run(init_op)

        #在训练过程中不再测试模型在验证数据上的表现，验证和测试的过程将会有一个独立的程序来完成。
        print("****************开始训练************************")
        for i in range(TRAINING_STEPS):
            xs, ys = mnist.train.next_batch( BATCH_SIZE )

            # 类似地将输入的训练数据格式调整为一个四维矩阵,并将这个调整后的数据传入sess.run过程
            reshaped_xs = np.reshape(xs, (BATCH_SIZE,
                                          mnist_inference.IMAGE_SIZE,
                                          mnist_inference.IMAGE_SIZE,
                                          mnist_inference.NUM_CHANNELS))
            train_op_renew,loss_value, step = sess.run([train_op, loss, global_step],feed_dict={x: reshaped_xs, y_: ys})
            # print("After %d training step (s) , loss on training batch is %g." % (step, loss_value))
            if i % 1000 == 0:
                # 每1000轮保存一次模型。
                # 输出当前的训练情况。这里只输出了模型在当前训练batch上的损失函数大小。
                # 通过损失函数的大小可以大概了解训练的情况。
                # 在验证数据集上的正确率信息会有一个单独的程序来生成。
                print ( "After %d training step (s) , loss on training batch is %g." % (step, loss_value))

                saver.save(sess,
                           r"C:\Users\Administrator\Desktop\code\tensorflow\test1\model\model.ckpt",
                           global_step = global_step)
                # 持久化一个简单的tensorflow模型。注意这里给出了global_step参数，这样可以让每个被
                # 保存模型的文件名末尾加上训练的轮数，比如“model.ckpt-1000” 表示训练1000轮之后得到的模型。
                # 通过 saver.save函数将tensorflow模型保存到了C:\Users\Administrator\Desktop\code\tensorflow\model\
                # model.ckpt文件中。每次保存操作会生成三个文件，这是因为tensorflow会将计算图的结构和图上参数取值分开保存。
                # 第一个文件为model.ckpt.meta，它保存了tensorflow计算图的结构；第二个文件为model.ckpt，这个文件中保存了
                # tensorflow程序中每一个变量的取值；最后一个文件为checkpoint文件，这个文件中保存了一个目录下所有的模型文件列表。

        print("*******************训练结束****************************")

# 主程序入口
def main(argv=None):
    """
    主程序入口
    声明处理MNIST数据集的类，这个类在初始化时会自动下载数据
    """
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
    if mnist != None:
        print("*************数据加载完毕*****************")
    train(mnist)

# TensorFlow提供的一个主程序入口，tf.app.run会调用上面定义的main函数
if __name__	 == '__main__':
    tf.app.run ()

      最后在mnist_eval.py文件中编写如下程序，选择迭代8000次后模型，在测试数据集上进行测试：

# -*- coding: utf-8 -*-

###################################
#########  作者：行歌   ############
#########  时间：2018.5.8  ########
######  email:[email protected]  ##
###################################

import time
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

###加载mnist_inference.py和mnist_train.py中定义的常量和前向传播的函数########
import mnist_inference
import mnist_train

#每10秒加载一次最新的模型，并在测试数据上测试最新模型的正确率
EVAL_INTERVAL_SECS = 10

def evaluate( mnist ):
    with tf.Graph().as_default() as g:   #将默认图设为g
        #定义输入输出的格式
        x = tf.placeholder(tf.float32, [mnist.validation.images.shape[0],
                                        mnist_inference.IMAGE_SIZE,
                                        mnist_inference.IMAGE_SIZE,
                                        mnist_inference.NUM_CHANNELS], name='x-input1')
        y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input')

        xs = mnist.validation.images
        # 类似地将输入的测试数据格式调整为一个四维矩阵
        reshaped_xs = np.reshape(xs, (mnist.validation.images.shape[0],
                                      mnist_inference.IMAGE_SIZE,
                                      mnist_inference.IMAGE_SIZE,
                                      mnist_inference.NUM_CHANNELS))
        validate_feed = {x: reshaped_xs, y_: mnist.validation.labels}

        #直接通过调用封装好的函数来计算前向传播的结果
        #测试时不关注过拟合问题，所以正则化输入为None
        y = mnist_inference.inference(x,None, None)

        #使用前向传播的结果计算正确率，如果需要对未知的样例进行分类
        #使用tf.argmax(y, 1)就可以得到输入样例的预测类别
        correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
        # 首先将一个布尔型的数组转换为实数，然后计算平均值
        # 平均值就是网络在这一组数据上的正确率
        #True为1，False为0
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

        #通过变量重命名的方式来加载模型
        variable_averages = tf.train.ExponentialMovingAverage(mnist_train.MOVING_AVERAGE_DECAY)
        variable_to_restore = variable_averages.variables_to_restore()
        # 所有滑动平均的值组成的字典，处在/ExponentialMovingAverage下的值
        # 为了方便加载时重命名滑动平均量，tf.train.ExponentialMovingAverage类
        # 提供了variables_to_store函数来生成tf.train.Saver类所需要的变量
        saver = tf.train.Saver(variable_to_restore) #这些值要从模型中提取

        #每隔EVAL_INTERVAL_SECS秒调用一次计算正确率的过程以检测训练过程中正确率的变化
        #while True:
        for i in range(2):    # 为了降低个人电脑的压力，此处只利用最后生成的模型对测试数据集做测试
            with tf.Session() as sess:
                #tf.train.get_checkpoint_state函数
                # 会通过checkpoint文件自动找到目录中最新模型的文件名
                ckpt = tf.train.get_checkpoint_state( r"C:\Users\Administrator\Desktop\code\tensorflow\test1\model")
                if ckpt and ckpt.model_checkpoint_path:
                    #加载模型
                    saver.restore(sess, ckpt.model_checkpoint_path)
                    #得到所有的滑动平均值
                    #通过文件名得到模型保存时迭代的轮数
                    global_step = ckpt.model_checkpoint_path.split('-')[-1]
                    accuracy_score = sess.run(accuracy, feed_dict = validate_feed)           #使用此模型检验
                    #没有初始化滑动平均值，只是调用模型的值，inference只是提供了一个变量的接口，完全没有赋值
                    print("After %s training steps, validation accuracy = %g" %(global_step, accuracy_score))
                else:
                    print("No checkpoint file found")
                    return
                time.sleep(EVAL_INTERVAL_SECS)
                # time sleep()函数推迟调用线程的运行，可通过参数secs指秒数，表示进程挂起的时间。

def main( argv=None ):
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
    evaluate(mnist)

if __name__=='__main__':
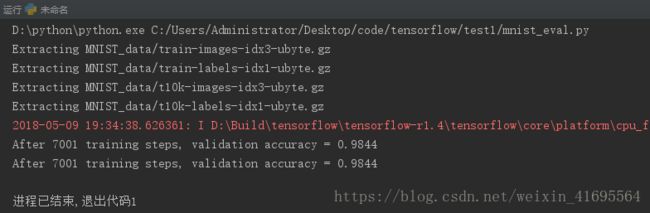
    tf.app.run()

运行测试文件，输出结果如下：

      准确率只有98.44%，我在这里只有训练了8000轮，如果训练30000轮，准确率会不会提升呢？

参考文献：

    [1]  郑泽宇著  《TensorFlow实战Google深度学习框架》

     [2] 黄文坚著  《TensorFlow实战》