图解二叉排序树的实现 (超详细)
从零开始一步步写出自己的二叉排序树,
即使没有数据结构的基础也能轻松理解
最近大半个月一直在看《C primer plus》,回顾一下几乎都快忘干净了的c语言。前面基础部分复习起来还是蛮快的,就是最后一章讲抽象数据类型有点难理解
这其中最难的应该就是二叉排序树(也叫二叉搜索树)了,我照着书中的源码敲了一遍,反复看了很多遍,虽然大致的过程是知道的,但是有些细节真的是有点难理解。于是自己以《C primer plus》中的代码为基准画图,以代码+图形+理解的方式解释二叉树的实现,最后确实效果很好,于是想把这个写下来,看能不能也帮到大家
如果能将二叉树搞清楚,那么链表、队列的实现应该也不在话下了
因为二叉树的实现确实有很多细节
.
.
这里先说明一下下面的导航栏 函数实现 部分括号里标记的接口函数和辅助函数是什么意思
- 接口函数
因为我们现在是在构建一个抽象数据类型,这些函数都是跟我们写的任务程序代码分开的,它的声明都在一个.h后缀文件中,实现过程都在另一个.c后缀文件中。所以接口函数是暴露给用户的,用户可以拿来使用的 - 辅助函数
辅助函数是帮助接口函数更好的完成任务(用 static 修饰,没有外部链接),使代码看起来更有条理,用户在使用过程中无法调用
有些太简单了可以跳过,希望能对你们有所帮助,如果我的表达有错误,欢迎来讨论、指正!!
导航
- 预备工作(图解)
- 函数实现
- 一、初始化
- InitializeTree函数 (接口函数)
- 二、 判断树是否为空
- TreeIsEmpty函数 (接口函数)
- 三、返回树的节点数
- TreeItemCount函数 (接口函数)
- 四、判断一个项是否在树中
- InTree函数(接口函数)
- SeekItem函数 (辅助函数)
- Compare函数 (辅助函数)
- 五、遍历树
- Traverse函数 (接口函数)
- InOrder函数 (辅助函数)
- 六、添加一个项
- AddItem函数 (接口函数)
- makeNode函数 (辅助函数)
- AddNode函数 (辅助函数)
- 七、删除一个项
- DeleteItem函数 (接口函数)
- DeleteNode函数 (辅助函数)
- 八、删除整个树
- DeleteTree函数 (接口函数)
- DeleteAllNodes函数 (辅助函数)
预备工作(图解)
在这里我以这样的方式来表示一个变量 地址、名称、值 之间的关系,以及取址、解引用、取值之间的关系。这样理解起来个人感觉比较直观
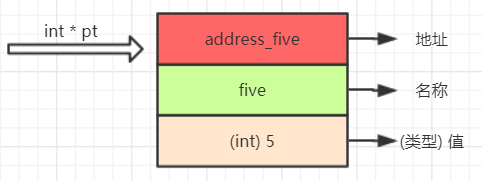

那么二级指针就应该这样表示
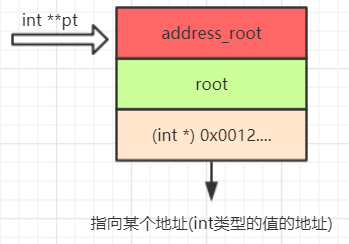
那么表示一个二叉树结构类型就是下面这样(该二叉树有一个指向根节点的root跟一个记录节点数的size),当然并不是所有的树都有一个记录节点数的变量。

那个root是指向Node类型(树中的节点)的变量的指针类型,而Node的结构定义如下,它包含一个自定义的数据,以及左子节点跟右子节点,分别指向两个节点,没有时为NULL

这其中的Item类型也是自己定义的,也就是我们的二叉树每一个节点所要保存的数据的类型
它有可能是一个整数,int类型的,也有可能是包含两个字符型的结构, 这取决于你想要存储什么样的数据

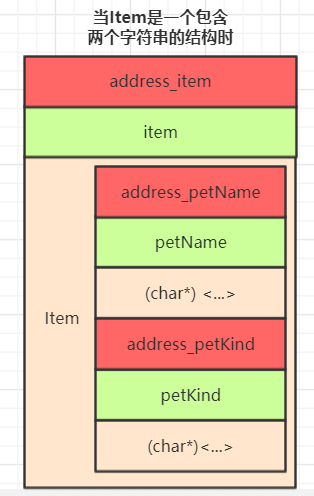
在《C primer plus》中作者的例子中,Item就是一个包含两个字符串的类型,分别储存一个宠物的名字跟品种
那么以上我们就用图形的方式解释了下面这些代码
#define SLEN 20
typedef struct item{
char petName[SLEN];
char petKind[SLEN];
} Item;
typedef struct node{
Item item;
struct Node * left;
struct Node * right;
} Node;
typedef struct tree{
Node * root; //根节点
int size; //树的节点数
} Tree;
像下面这样,四个节点被连接起来组成了一个这样的二叉树

二叉排序树的定义:
- 若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的节点。
以上,我们的预备工作就做好了,下面进入函数的实现部分
函数实现
我将实现比较简单的几个函数放在前面,它们不需要图解就能很好的理解
这里的函数都是根据《C primer plus》里的代码而来的,有些并不是二叉树必需的,有些没有被包含,但是你如果把这些函数理解了,其他的应该也没有太大的问题
.
一、初始化
.
InitializeTree函数 (接口函数)
实现代码
void InitializeTree(Tree * ptree){
ptree->root = NULL;
ptree->size = 0;
}
我们只要传入树的地址,将树的两个变量初始化就OK了
.
.
.
二、 判断树是否为空
.
TreeIsEmpty函数 (接口函数)
实现代码
bool TreeIsEmpty(const Tree *ptree){
return ptree->root == NULL;
}
只要树的root变量指向的是NULL,证明树的根节点都没有,也就是空树
.
.
.
三、返回树的节点数
.
TreeItemCount函数 (接口函数)
实现代码
int TreeItemCount(const Tree *ptree){
return ptree->size;
}
.
.
下面的几个函数实现起来相对就没有那么简单了
分别是: 判断项是否在树中、遍历树、添加项、删除项、删除树
.
四、判断一个项是否在树中
.
InTree函数(接口函数)
其实它的功能是由一个辅助函数SeekItem来实现的
实现代码
bool InTree(const Item *pi, const Tree *ptree){
return (SeekItem(pi, ptree).child == NULL) ? false : true;
}
流程图如下(这里item = *pi, tree = *ptree)
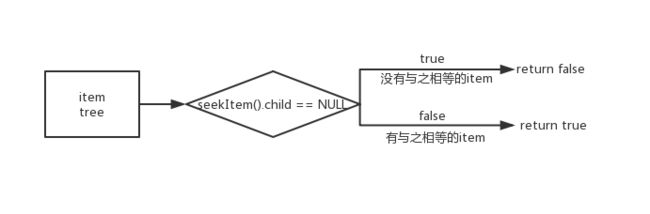
下面我们就来剖析一下辅助函数SeekItem的实现
.
.
SeekItem函数 (辅助函数)
我们应该要牢记二叉排序树的定义
- 其左子节点的item < 它的item < 右子节点的item*。这样才能保证二叉树的有序型
.
这里的大于号、小于号并不是仅仅指数字之间的比较大小符号,不然像我们本例中item是一个含有两个字符串的数据,岂不是比较不了。当然我们另有办法,构造一个比较函数来充当我们的比较符, 就是下面要说的Compare函数
.
.
Compare函数 (辅助函数)
书中的实现是用两个函数ToLeft, ToRight来实现的,我对其进行了一些修改,用一个函数即可完成,下面是Compare函数的实现
static int Compare(const Item *pi1, const Item *pi2){
int comp;
if ((comp = strcmp(pi1->petName, pi2->petName)) != 0)
return comp;
else
return strcmp(pi1->petKind, pi2->petKind);
}
不了解strcmp函数及其返回值的小伙伴可以自行去了解下,这里我就不作解释了,这样,如果第一个item“小于”第二个item,就会返回一个负值,如果“大于”,就会返回一个正值,如果“等于”,就会返回0;
这样实现的好处是,如果Item结构类型中有更多个成员时,我们只要在该函数中添加 else if ,变换顺序等,就能轻松改变比较的方式
.
.
好了,我们接下来就可以看看SeekItem函数的原型了
static Pair SeekItem(const Item *pi, const Tree *ptree);
这里解释下这个Pair类型的返回值是什么?
SeekItem函数不仅要找到目标节点(item与我们要找的item相等的节点),而且要将它的父节点一并返回,为什么要这样呢?因为后面要讲的删除节点函数中我们要用到它的父节点,这里就不过多介绍了
Pair结构中包含两个节点的地址,分别是目标节点的父节点以及目标节点的地址
typedef struct pair{
Node * parent;
Node * child;
} Pair;
.
.
看了以上的内容,我们就能来看看SeekItem函数的具体实现了
static Pair SeekItem(const Item *pi, const Tree *ptree){
Pair look;
look.parent = NULL; //初始时让父节点地址为NULL
look.child = ptree->root; //让"目标节点"地址为根节点(root为根节点地址)
if (look.child == NULL)
return look; //是空树,提前返回
while (look.child != NULL){ //也可以使用递归
int cmp_result = Compare(pi, &(look.child->item)); //比较
if (cmp_result < 0){ //如果要找的item比当前的"目标节点"item小
look.parent = look.child;
look.child = look.child->left;
}
else if (cmp_result > 0){
look.parent = look.child;
look.child = look.child->right;
}
else //如果前两种情况都不满足,则必定相等
break; //look.child 目标项的节点
}
return look; //成功返回
}
下面我们以实际的树来模拟这个过程, 为了简易,我们此时将Item类型设置为int类型
假设我们在下面这个树中查找5(Item类型)

过程:
- 首先创建Pair类型变量look,并且使look.parent = NULL, look.child 指向根节点(即7所在的节点)
- 比较5跟look.child(即根节点)的item(即7)
- 得到负值,说明5比7小,则调整look.parent指向根节点,look.child指向4所在节点
- 比较5跟look.child(即4所在节点)的item(即4)
- 得到正值,说明5比4大,则调整look.parent指向4所在节点,look.child指向5所在节点
- 比较5跟look.child(即5所在节点)的item(即5)
- 得到0,说明相等,匹配成功,跳出循环,返回look(此时parent指向4所在节点,child指向5所在节点)
大家也可以自己试试去找一个树中不存在的item,最后child指向的一定是NULL
那么SeekItem函数我们就解读完毕了,InTree函数也就明了了,child返回NULL就是没有,不是NULL就证明有
.
.
.
五、遍历树
.
Traverse函数 (接口函数)
实现代码
void Traverse(const Tree *ptree, void (*pfun)(Item item)){
if (ptree != NULL)
InOrder(ptree->root, pfun);
}
这里pfun指向的是一个接受Item类型的数据的函数
遍历函数也是通过一个辅助函数InOrder来实现的(当然你也可以把InOrder函数内的代码搬到Traverse函数中)
.
.
InOrder函数 (辅助函数)
那么我们来看看InOrder函数的实现
static void InOrder(const Node *root, void(*pfun)(Item item)){
if (root != NULL){
InOrder(root->left, pfun);
(*pfun)(root->item);
InOrder(root->right, pfun);
}
}
是不是感觉好像很简单,就这么几行代码,说实话我第一次看到的时候确实感觉确实很神奇,递归真的是非常强大
书中的实现是用中序遍历,也就是上面的代码,那么前序遍历、后序遍历怎么实现呢,我们只需要把(*pfun)(root->item);这行代码换位置即可,放到这三行代码的最前面就是前序遍历,放到最后面就是后序遍历
如果大家感觉还是很迷糊,这个过程,我画了个图(按中序遍历来画的),方便大家能够直观地看到递归过程(根据箭头的走向)
我们还是以这个item为数字的树为例,三个连续的圆圈表示那三行代码
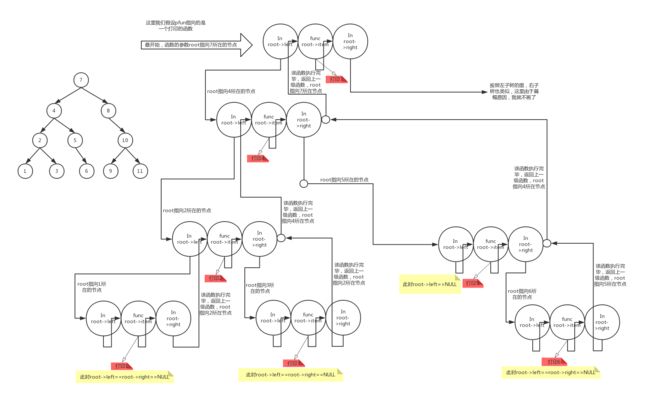
最后打印顺序就是1,2,3,4, 5,6, 7,8, 9,10, 11
大家也可以自己动手画画前序遍历,后序遍历
其实感觉在二叉排序中递归就是一种大化小,化到不能再小为止的思想, 每一次递归所做的事情也是一致的
递归进入第一层的时候确定了下面这三个部分的顺序(从左至右)

进入第二层时确定了下面这三个部分的顺序

进入第三层的时候确定下面这两个子树的各部分的顺序
这样,树的根节点的左子树的顺序就彻底排好了(按这些图片从下往上写:12345678…)
其实当我们这样去想的时候,我们的思维就是递归思维了 (这词是我自己瞎编的哈哈哈)
然后同理,右子树排好之后,整个树的顺序也就确定了
所以今后我们看到一个树,可以根据这样的思路迅速写出它的遍历顺序
到这儿,我们的遍历函数也就结束了
.
.
.
六、添加一个项
.
AddItem函数 (接口函数)
它的功能是由另外两个辅助函数makeNode, 以及AddNode辅助完成的
实现代码
bool AddItem(const Item *pi, Tree * ptree){
Node * new_node;
if (InTree(pi, ptree)){
fprintf(stderr, "Attempted to add duplicate item\n");
return false; //重复项,提前返回
}
new_node = MakeNode(pi); //指向新节点
if (new_node == NULL){
fprintf(stderr, "Couldn`t create node\n");
return false; //创建新节点失败,提前返回
}
/* 成功创建一个新节点 */
ptree->size++;
if (ptree->root == NULL) //情况1:树为空
ptree->root = new_node; //新节点为树的根节点
else //情况2:树不为空
AddNode(new_node, ptree->root); //在树中添加新节点
return true; //成功返回
}
流程图如下,其中item = *pi, tree = *ptree

那么我们就来看看这两个辅助函数是如何实现的
.
.
makeNode函数 (辅助函数)
它将一个数据项item包装成一个节点并返回,节点的内存是用malloc申请的
如果申请失败了,那么返回的new_node就是NULL
实现代码:
static Node * MakeNode(const Item *pi){
Node * new_node;
new_node = (Node *) malloc(sizeof(Node));
if (new_node != NULL){
new_node->item = *pi;
new_node->left = new_node->right = NULL;
}
return new_node;
}
可以用下面这个图来更直观地看到该函数是在干什么,其中item = *pi
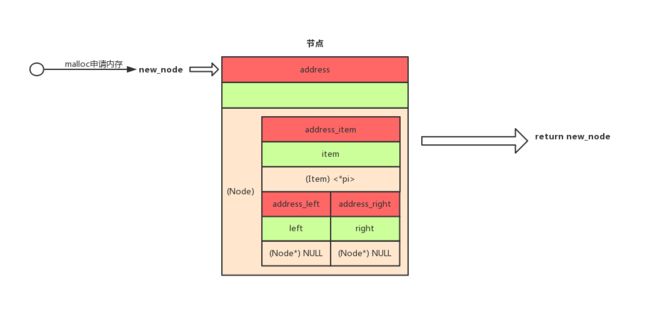
.
.
AddNode函数 (辅助函数)
该函数的作用是把已经包装好的节点连接到我们的二叉排序树中去
这里我们依然要记得二叉排序树的定义,那么我们在添加节点之后依然要遵守这个定义,否则不就乱套了吗
我们在前面已经排除了树是空树,排除了是重复项
这里我们给出两种实现,循环版跟递归版
实现代码(循环版):
static void AddNode(Node * new_node, Node * root){
Node * root_ = root;
while (true){
int cmp_result = Compare(&new_node->item, &root_->item);
if (cmp_result < 0){
if (root_->left == NULL){ //有空子节点可以连接
root_->left = new_node; //把节点添加到此处
break;
}
else
root_ = root_->left;
}
else if (cmp_result > 0){
if (root_->right == NULL){
root_->right = new_node;
break;
}
else
root_ = root_->right;
}
}
}
实现代码(递归版):
static void AddNode(Node * new_node, Node * root){
if (Toleft(&new_node->item, &root->item)){
if (root->left == NULL) //有空子节点(停止条件)
root->left = new_node; //把节点添加到此处
else
AddNode(new_node, root->left); //否则处理该子树
}
else if (ToRight(&new_node->item, &root->item)){
if (root->right == NULL) //停止条件
root->right = new_node;
else
AddNode(new_node, root->right);
}
}
可以看到,无论是怎么实现,这个函数就是要在不破坏二叉排序树定义的情况下,一步步向下去寻找可以被连接的位置
我们依旧用一个Item类型为int类型的二叉排序树来模拟这个过程,让理解更加深刻
以下面这个二叉排序树为例,我们假设要将一个item为5.5的节点new_node加入到这个树

过程:
- 开始时, root_开始指向7所在的节点
- 首先我们将new_node->item(即5.5)与root_->item(即7)比较
- 比它小,但是它的左节点已经被占据了,于是我们此时将4所在的节点当做根节点(root_),再让5.5与其比较
- 比它大,但是它的右节点已经被占据了,于是我们此时将5所在的节点当做根节点,再让5.5与其比较
- 比它大,但是它的右节点已经被占据了,于是我们此时将6所在的节点当做根节点,再让5.5与其比较
- 比它小,而且它的左节点指向NULL,于是我们此时就可以将它的左节点指向new_node,大功告成
- 最终,我们将这个new_node连接到了6所在的节点的左子节点上,我们可以看到,这个定义我们并没有被打破
.
.
.
七、删除一个项
.
DeleteItem函数 (接口函数)
它的功能是由另外两个辅助函数SeekItem, 以及DeleteNode辅助完成的
SeekItem我们在前面已经介绍过了,它返回的目标节点的父节点的地址parent在这里派上了大用场
我们始终要记住二叉排序树的排序规则,删除以后依旧不能破坏定义
实现代码:
bool DeleteItem(const Item *pi, Tree * ptree){
Pair look;
look = SeekItem(pi, ptree);
if (look.child == NULL)
return false; //没有匹配到节点
if (look.parent == NULL) //证明要删的项在根节点中,删除根节点项
DeleteNode(&(ptree->root));
else if (look.parent->left == look.child)
DeleteNode(&(look.parent->left));
else
DeleteNode(&(look.parent->right));
ptree->size--;
return true;
}
流程图如下:(其中item = *pi, tree = *ptree)

这里我们可以对照前面的一张图来理解,就可以更清晰地看到过程
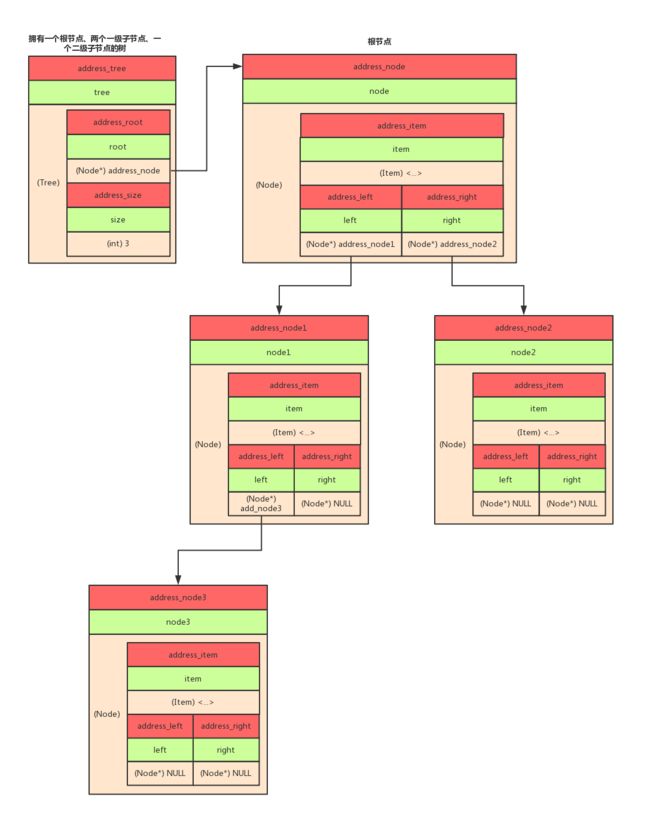
假设我们要删除的item等于节点node1中的item,那么意味着我们要把node1删除(即释放掉当初建立它所申请的内存)
模拟过程:(请对照上面的图)
- 我们已经匹配到了这个节点,此时SeekItem函数返回的两个节点的地址,parent等于根节点node的地址,child等于node1的地址
- 我们首先使parent->left = address_node3(即parent->left->left), 让根节点的左节点指向被删节点的左子节点,然后释放掉node1的内存,就大功告成了
- 由于上一步的操作是交给辅助函数DeleteNode来完成的,所以我们要把parent->left的地址(在这里就是根节点中的address_left)传给DeleteNode函数,由于parent->left是Node*类型的变量,所以DeleteNode接收的参数就是Node**类型的
很显然,遇到上面的这个情况是我们走运,因为我们要删除的这个节点它只有一个子节点,这样我们相当于只要通过改变的父节点的left指针或者right指针跳过这个被删除的节点就可以了,但是要是被删除的这个节点有两个子节点我们该怎么办呢?
这就要看我们的DeleteNode函数的设计了!!!
.
.
DeleteNode函数 (辅助函数)
释放一个节点内存,我们要根据这个节点的情况来来决定是如何处理,分为四种情况
- 这个节点没有任何子节点,是个叶子节点,那么我们直接释放就可以了
- 这个节点拥有一个子节点,且有一个左子节点,就像我们在前面举的例子那样,像那样处理就可以
- 这个节点拥有一个子节点,且有一个右子节点,操作过程同上,代码中只要把left改成right即可
- 这个节点拥有两个子节点,显然这种情况是最难处理的
下面我们看看代码的实现,后面再仔细介绍:
PS:ptr是指向目标节点的父节点指针成员(letf/right)的地址,*ptr是它的成员left/right的值,这个值同时又是目标节点的地址
(这里大家想不清楚可以把上面那张图以及我举的例子拿来看看)
static void DeleteNode(Node **ptr){
/* ptr 是指向目标节点的父节点指针成员(letf/right)的地址 */
Node * temp;
if ((*ptr)->left == NULL && (*ptr)->right == NULL){ //要释放的节点是叶子节点
free(*ptr);
}
else if ((*ptr)->left == NULL){
temp = *ptr;
*ptr = (*ptr)->right;
free(temp);
}
else if ((*ptr)->right == NULL){
temp = *ptr;
*ptr = (*ptr)->left;
free(temp);
}
else{ //被删除的节点有两个子节点
/* 找到重新连接右子树的位置 */
for (temp = (*ptr)->left; temp->right != NULL; temp = temp->right)
continue;
temp->right = (*ptr)->right;
temp = *ptr;
*ptr = (*ptr)->left;
free(temp);
}
}
有了前面的铺垫,前面三种情况应该是好理解的。不好理解的就是这最后一种情况,有两个子节点的情况
下面我依然用举例子的方式来向大家解释为什么是这样处理
我仍旧用下面这个二叉排序树来说明
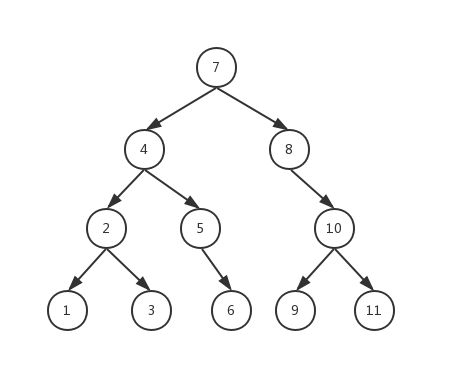
假如我们要删除4所在的节点,我们应该怎么做呢?
- 此时SeekItem函数一定给我们返回了7所在的节点的地址、以及4所在的节点的地址
- 首先,我们要把7所在的节点的左子节点重定向为2所在的节点
- 然后,我们要把3所在的节点的右子节点指向5所在的节点(为什么是连在3所在的节点,原因我们后面解释),这在代码中,就体现为不停的寻找2所在的节点右子节点的右子节点的右…, 在这里就是从2节点出发,一直找,最后就找到3所在的节点,该节点的右子节点指向NULL,满足我们的需要,此时就形成了下面这样的局面
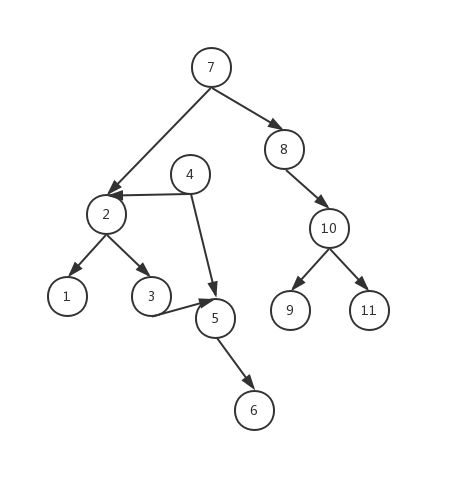
- 然后我们就可以放心的释放掉4所在的节点所申请的内存(在形成上面的局面之前你应该先把4所在的节点的地址记录下来,不然这时候你就没办法再得到它的地址了,也就没办法释放内存了,因为已经没有任何指针指向它了)
最后我们来解决这其中你们可能想问的两个问题
问题一、为什么是让5所在的节点连接到3所在的节点的右子节点上(即下面所标记的子树的最右下角)
我们暂且把下面这个被标记的子树命名为A子树
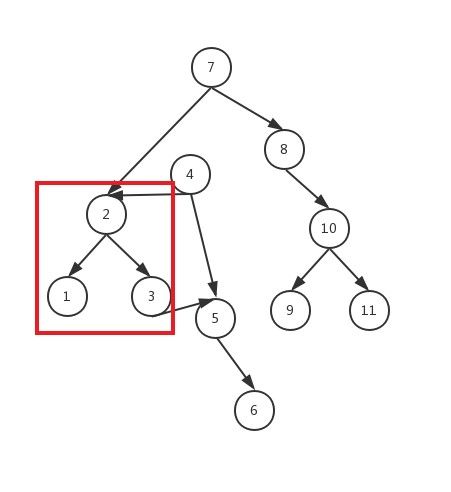
不知道大家有没有发现,对于二叉排序树来说,最左下角的值是最小的,最右下角的值是最大的(二叉排序树的定义所导致的,小的到左边,大的到右边),而且,5所在的节点以及它所有的子代节点的项肯定都是比4大的,A子树中的所有节点的项肯定都是比4小的,所以5跟A子树中的节点的项比,肯定是最大的。而且我们连接的时候只要关注5所在的节点就好了,因为5这个节点及其它的子孙节点的顺序已经是排好了的。所以我们应该把5所在的节点连接到A子树的最右下角
问题二、为什么我们要让7所在的节点的左子节点重定向为2所在的节点,而不是5所在的节点?
其实这样做同样可以,只要后面的操作也换一下就行,当我们选取2所在的节点时,我们要把5所在节点连接到A子树的最右下角,那么当我们选取5所在的节点时,我们应该就应该把2所在的节点连接到B子树(5, 6所组成的子树)的最左下角
上面的种种操作,其实最终目的,就是删除节点之后,不打破二叉排序树的定义
.
.
.
八、删除整个树
.
DeleteTree函数 (接口函数)
它的实现是靠辅助函数DeleteNode函数来实现的
代码实现:
void DeleteTree(Tree * ptree){
if (ptree->root != NULL)
DeleteAllNodes(ptree->root);
ptree->root = NULL;
ptree->size = 0;
}
流程图如下
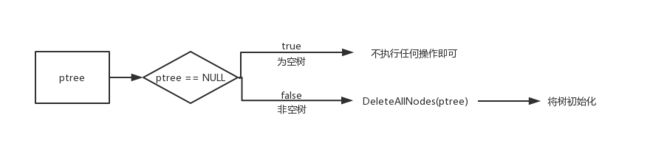
那么我们来介绍一下这个辅助函数DeleteAllNodes
.
.
DeleteAllNodes函数 (辅助函数)
我觉得应该先看看它是怎么实现的
static void DeleteAllNodes(Node * ptr){
Node * pright;
if (ptr != NULL){
pright = ptr->right;
DeleteAllNodes(ptr->left);
free(ptr);
DeleteAllNodes(pright);
}
}
我们可以看到也是一个递归,而且你有没有发现它非常像前面的那个遍历辅助函数InOrder(中序遍历),我们把它的代码放到这里对比一下
static void InOrder(const Node *root, void(*pfun)(Item item)){
if (root != NULL){
InOrder(root->left, pfun);
(*pfun)(root->item);
InOrder(root->right, pfun);
}
}
唯一有点不同,就是DeleteAllNodes函数它在释放内存之前将它的右子节点记录了下来
我们来看看它为什么要这样做
其实我觉得可以把前面解释递归的那张图拿来

这里我们把中间那个圆圈,也就是要执行的函数,换成free(), 那么你看我们在执行释放root操作后,我们还能通过root->right去释放别的节点内存吗,显然不能,因为root所指向的节点已经被销毁了,所以这个时候,我们要在其销毁之前把root->right这个地址记录下来
我们再从另外一个角度来看这个问题(也许书中的代码也许可以换换)
我们来看下面这个二叉树

我们这里的DeleteAllNodes函数,它的释放顺序类似于中序遍历: GDHBEIACJFK
过程:
- 先记录G所在节点的右子节点(由于是NULL,所以后面不触发函数), 释放G所在节点内存
- 先记录D所在节点的右子节点(即H所在节点),然后释放D所在节点内存
- 先记录H…
- …
也就是说这种释放顺序“根节点”先与右子节点删除,所以假如我们让两个子节点先与“根节点”删除,我们就不要另外一个变量来记录了
这就类似后序遍历了:GHDIEBJKFCA
我们是由子节点一步步向上删除的,也就无需记录了
新的代码如下
static void DeleteAllNodes(Node * ptr){
if (ptr != NULL){
DeleteAllNodes(ptr->left);
DeleteAllNodes(ptr->right);
free(ptr);
}
}
.
.
.
.
到这儿,就介绍完了所有的函数实现,不知道有没有解开大家的一些困惑,如果能帮到大家,那就太好了
其实大家如果搞明白了二叉排序树的实现过程,就可以自己去对二叉排序树的实现进行一些小改造(比如加个能返回树的深度的函数啥的),也不至于在报错的时候一头雾水
在二叉排序树的实现中,最重要的就是递归了
当然我也在其它的博客中看到过非递归版的实现,要涉及到入栈出栈的操作,比递归复杂一些
ps:这其中对树的size变量(节点数)的变更并没有在流程中画出,它其实就只在两个地方有变更,一个是成功添加了一个item时,另一个是成功删除了一个item时
完整源代码如下:
二叉排序树.h头文件与.c文件
如需转载,请注明出处
链接:https://blog.csdn.net/weixin_43585353/article/details/105903062

