题目总结--“字节跳动-文远知行杯”广东工业大学第十四届程序设计竞赛

    两个多月没练了，感觉ACM已经渐行渐远，考研的压力一吨吨袭来。  趁着周末打一场比赛热热手，省赛不要太难看。。。“字节跳动-文远知行杯”广东工业大学第十四届程序设计竞赛 这套题难度挺大的，一开场就有些惊慌失措（第1题签到题不会）。结束时只做了7个，抽时间再补一下吧。

给出竞赛链接，下面就不贴题面了。http://acm.hdu.edu.cn/contests/contest_show.php?cid=843

上面如果进不去的话，进题库第55页，对应题号6461~6470 http://acm.hdu.edu.cn/listproblem.php?vol=55

 

【problem 1001】

概率问题？？？？不会，真的不会。代码都不想写！答案：输出4个1.00\n

【problem 1002】

题意：一个螺旋线，从内向外螺旋，依次穿过越来越大的正方形（图形很优美啊，大矩形边长满足斐波那契数列）。最里面开始的两个小正方形边长都是1，再往外的正方形边长是 2  3  5  8  13，（这不是斐波那契数列吗！？）。然后，给出一个类似带分数的形式x+y，其实就是第x*4+y个正方形（读了半天才读懂，出题人真会折磨人，应该是直接给出项数就不好玩了）。问从a+b个正方形到第c+d个正方形的面积之和=？

分析：由于数据量不大，直接打表，设斐波那契数列为f[i]，我们求得f[i]*f[i]的前缀和 即面积前缀和。

#include
using namespace std;
typedef long long ll;
const int MAX=1e6+5;
const int mod=192600817;
ll f[201010];
ll f2[201010];
ll sf2[201010];

int main()
{
    f[0]=f[1]=1;
    for(int i=2;i<101000;i++)f[i]=(f[i-2]+f[i-1])%mod;
    for(int i=0;i<101000;i++)
    {
        f2[i]=f[i]*f[i]%mod;
        if(i==0)sf2[i]=1;
        else sf2[i]=(sf2[i-1]+f2[i])%mod;
    }

    int Q,a,b,c,d;
    while(cin>>Q)
    {
        while(Q--)
        {
            scanf("%d%d%d%d",&a,&b,&c,&d);
            ll L=a*4+b;
            ll R=c*4+d;
            if(L>R)swap(L,R);
      //      cout<<" **************  "<

【problem 1003】超级无敌简单题

分析：如题所述的鸽子数。数据量也不大，直接暴力标记每一个数是不是鸽子数，然后把鸽子数收集到一个数组里再接收询问即可。   其实刚开始以为这样会超时，想的方法是：建图，设数字x的下一步是y，则由建有向边y->x，建图后，从1出发进行搜索，凡是能到达的点，均为鸽子数，然后把鸽子数收集到数组里接受询问即可。比较懒没去实现，建议实现一下，如思路有错，恳请评论区指出。

这是暴力代码：

#include
using namespace std;
typedef long long ll;
const int MAX=1e6+1e5;
bool isg[MAX]={0,1};
int vis[MAX];
int sta[MAX];

bool dfs(ll num,int beg)
{
    if(vis[num]==beg)return false;
    vis[num]=beg;
    if(isg[num])return true;

    ll res=0;
    for(ll x=num;x;x/=10)res+=(x%10)*(x%10);
    return isg[num]|=dfs(res,beg);
}

int main()
{
    for(int i=1;i>T;T--;)
    {
       scanf("%d",&n);
       printf("%d\n",sta[n-1]);
    }
}

【problem 1004】免费送气球

分析：这个挺有难度的。题目虽然说每次插入的first个second是插到尾部，我们默认插入后让它有序，就可以。但是有数数字太大了，太多了，想存下来不可能。庆幸的是数字种数不会超过操作次数1e5。数字太多了？我们只保存每个数字有多少个就好了。数字太大了？离散化之后就可以作下标了。

因此，我只需要保存①每个数字的个数②数字的前缀和，这个前缀和把每种数字看做一个点。

树状数组在合适不过了，搞两个树状数组分别存①和②

当插入first个second的时候，相当于树状数组点更新

询问区间和时，分三段，左段是first所在数字（二分查找找出来），右段second所在数字（二分查找），中段是内包的那些数字，用树状数组②来查询。

#include
using namespace std;
typedef long long ll;
const int MAX=1e6+5;
const int mod=1000000007;

struct query{
    ll t,f,s;
}q[MAX];
int T;
ll ha[MAX],top;
int pos(ll num)
{
    return lower_bound(ha+1,ha+1+top,num)-ha;
}


ll c1[MAX]; //个数
ll c2[MAX]; //和
void add1(int k,ll num)
{
    for(;k<=top;k+=k&-k)
    {
        c1[k]+=num;
    }
}
ll Qsum1(int k)
{
    ll ans=0;
    for(;k;k-=k&-k)ans+=c1[k];
    return ans;
}

void add2(int k,ll num)
{
    for(;k<=top;k+=k&-k)
    {
        c2[k]+=num;
        c2[k]%=mod;
    }
}
ll Qsum2(int k)
{
    ll ans=0;
    for(;k;k-=k&-k)ans=(ans+c2[k])%mod;
    return ans;
}



int getBlock(ll pos)
{
    int l=1,r=top,mid;
    while(l>1;
        if(Qsum1(mid)>=pos)r=mid;
        else l=mid+1;
    }
    return r;
}

int main()
{
    cin>>T;
    top=0;
    for(int i=0;i

【problem 1005】

还没做出来。。。反正不会，瞎扯两句。感觉：第一个三角形以一点为中心，得出另外三点的向量值，第二个三角形得出对应的两个点的向量值，剩下的一个向量值就可以通过某种*****（我不知道的）的线代公式算出来。

【problem 1006】

I cat't solve it

【problem 1007】简单数学题

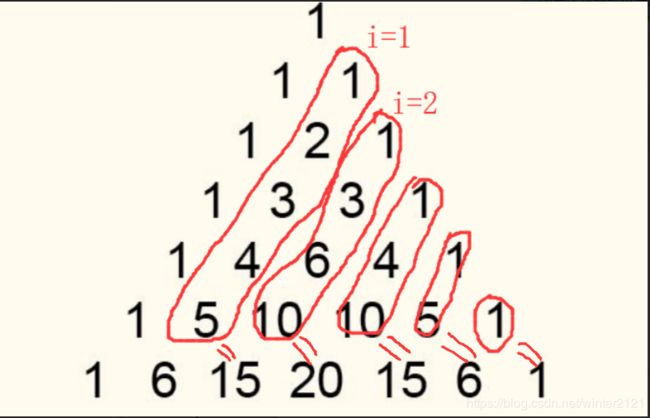
分析：题目给的式子很复杂，但其实好好分析一下，配合杨辉三角，就能化简成一个通项公式。画一个杨辉三角！！

第一步》看最内层，以n=5为例，你能把i=1的那些数圈起来吗？i=2，3...同理分别圈起来，也就是如下：

然后你会发现一个惊人的秘密：圈起来的每一组的和=第n+1行的第i+1个数！

这最内层就化简成了，到此时，原式=

第二步》问题变成了第n+1行每个数乘上 i  减掉左端那个1。不难发现，杨辉三角每一行都是对称的，上式中，每个数要乘以i，然后我们把乘上i的这行数，复制一行逆序的，这个逆序处理对于对称的组合数不起作用，但是对于i有用。把这两行数相加为sum，那么我们的答案就等于sum/2再减掉多加的开头两个数。（这两行数相加后，i和n-i-1对应位置正好得n-1）

第三步》不难发现，杨辉三角第n行的和=2的n次方。因此

然后和样例对比发现，答案

#include
using namespace std;
typedef long long ll;
const int mod=1000000007;

ll qpow(ll n,ll m)
{
    n%=mod;
    ll ans=1;
    for(;m;m>>=1)
    {
        if(m&1)ans=ans*n%mod;
        n=n*n%mod;
    }
    return ans;
}

int main()
{
    ll n;
    while(scanf("%lld",&n)!=EOF)
    {
        ll ans=qpow(2,n)*((n-1)%mod)%mod+1;
        printf("%lld\n",ans%mod);
    }
}

【problem 1008】

分析：这个没什么简单好办法，我用的dfs剪枝一下。以n=28为例的搜索树如下，按bfs搜可得自然序列，按dfs搜，可得字典序序列。

#include
using namespace std;
typedef long long ll;
const int MAX=1e6+5;

int f[20]={0,1,11,111,1111,11111,111111,1111111};

int a[20],top;
int mark;
int dfs(int n,int dep,ll num,int in)
{
    if(--mark==0)return num;
    for(int i=(dep==1);i<=9;i++)
    {
        if(num*10+i>n)continue;
        int nin=in;
        if(nin==0&&a[dep]!=i) nin=i

【problem 1009】

不会

【problem 1010】

分析：题意很简单。，直接矩阵快速幂得fn即可

#include
using namespace std;
typedef long long ll;
const int mod=123456789;

struct matrix{
    ll a[11][11]; //begin with 1
    int r,c;
    matrix(int n,int m):r(n),c(m){memset(a,0,sizeof(a));}
    ll* operator[](int x){return a[x];}
    friend matrix operator*(matrix A,matrix B)
    {
        matrix C(A.r,B.c);
        for(int i=1;i<=A.r;i++)
            for(int j=1;j<=B.c;j++)
                for(int k=1;k<=A.c;k++){
                    C[i][j]+=(A[i][k]*B[k][j])%mod;
                    C[i][j]+=mod;
                    C[i][j]%=mod;
                }
        return C;
    }
};
matrix qpow(matrix A,ll m)//方阵A的m次幂
{
    matrix ans(A.r,A.c);
    for(int i=1;i<=A.r;i++) ans.a[i][i]=1; //单位矩阵
    while(m)
    {
        if(m&1)ans=ans*A;
        A=A*A;
        m>>=1;
    }
    return ans;
}

int main()
{
    ll T,n;
    for(cin>>T;T--;)
    {
        scanf("%lld",&n);
        matrix A(6,6);
        A[1][1]=1;
        A[1][2]=2;
        A[1][3]=1;
        A[1][4]=3;
        A[1][5]=3;
        A[1][6]=1;
        A[2][1]=1;
        A[3][3]=1;
        A[4][3]=1;
        A[4][4]=1;
        A[5][3]=1;
        A[5][4]=2;
        A[5][5]=1;
        A[6][3]=1;
        A[6][4]=3;
        A[6][5]=3;
        A[6][6]=1;
        matrix X2(6,1);
        X2[1][1]=2;
        X2[2][1]=1;
        X2[3][1]=1;
        X2[4][1]=2;
        X2[5][1]=4;
        X2[6][1]=8;

        matrix Xn=qpow(A,n-2)*X2;
        printf("%lld\n",Xn[1][1]);
    }
}