多项式的表示方法
系数表示法:
$$f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n$$
点值表示法:
$$f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),\cdots,(x_n,f(x_n))\}$$
多项式乘法与DFT
设我们已知两个点值表示法的多项式$f(x),g(x)$:
$$f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),\cdots,(x_n,f(x_n))\}$$
$$g(x)=\{(x_0,g(x_0)),(x_1,g(x_1)),(x_2,g(x_2)),\cdots,(x_n,g(x_n))\}$$
设两个多项式相乘和结果是$h(x)$:
$$h(x)=\{(x_0,f(x_0)g(x_0)),(x_1,f(x_1)g(x_1)),(x_2,f(x_2)g(x_2)),\cdots,(x_n,f(x_n)g(x_n))\}$$
是不是感觉多项式乘法能$O(n)$过。
你想多了。。。
如何将系数转点值?
朴素的系数转点值叫做DFT(离散傅里叶变换),点值转系数叫做IDFT(离散傅里叶逆变换),计算式DFT,IDFT仍然需要$O(n^2)$。
难道就没有其他办法了吗?
当然有。FFT和IFFT闪亮登场,我们只要$O(n\log(n))$,就可以完成双方的转换。
单位复根
事实上,对于多项式系数转点值,我们可以随意取n个不同的x,但这种暴力法太慢。但我们可以取一些神奇的点,将满足$\omega ^n=1$的值作为带入的点。这就是离散傅里叶变换的神奇之处了,取的点不是实数,而是复数。
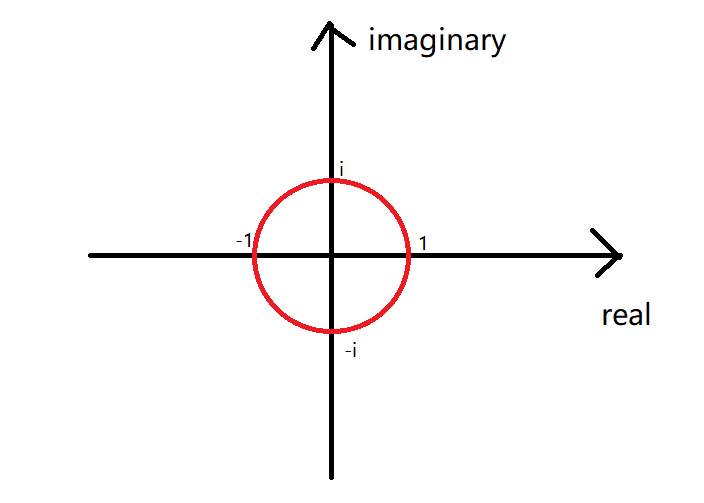
求解$\omega ^n=1$
对于所有的解都可以在下图的圆上得到:
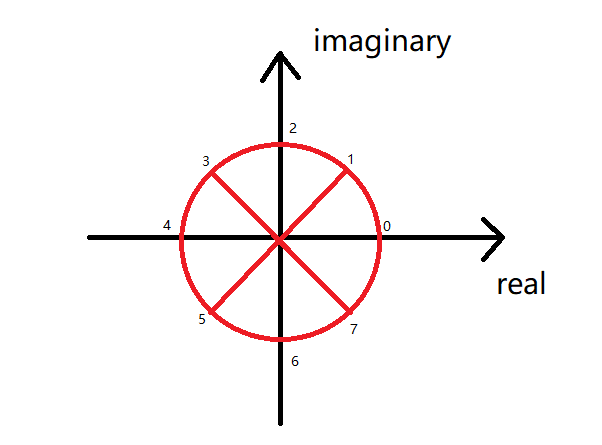
以$n=8$为例,即$\omega ^8=1$
将一个圆分成8份,我们可以得到8个解:$\omega _8^0,\omega _8^1,\omega _8^2,\omega _8^3,\omega _8^4,\omega _8^5,\omega _8^6,\omega _8^7$
即:$$\omega _n^k=\cos{\frac{2\pi }{n}k}+i\sin{\frac{2\pi }{n}k}$$
性质:
$(1)~~\omega _{an}^{ak}=\omega _n^k$
$(2)~~\omega _n^{k-\frac n2}=-\omega _n^k$
$(3)~~\omega _n^k=\omega _n^{k\%n}$
$(4)~~(\omega _n^k)^p=\omega _n^{kp}$
FFT(快速傅里叶变换)
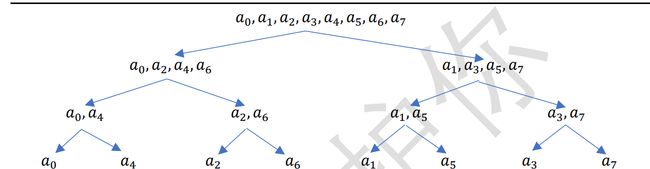
我们以多项式$f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7$为例:
$\begin{align*} f(x)&=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7 \\ &=a_0+a_2x^2+a_4x^4+a_6x^6+x(a_1+a_3x^2+a_5x^4+a_7x^6) \end{align*}$
$令A^{[0]}(x)=a_0+a_2x+a_4x^2+a_6x^3,A^{[1]}(x)=a_1+a_3x+a_5x^2+a_7x^3$
$则f(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)$
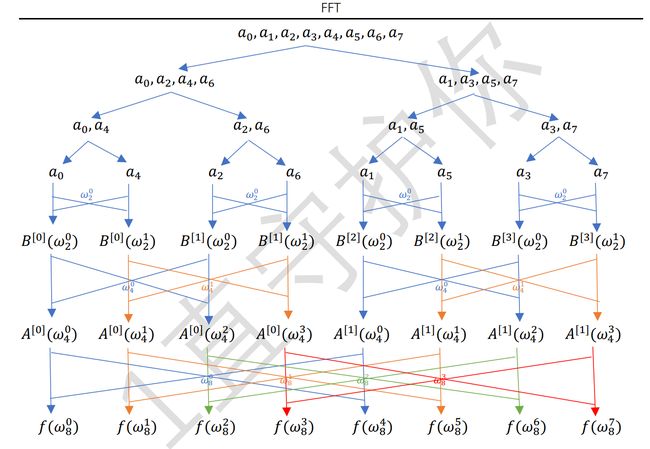
$\begin{align*} &f(\omega _8^0)=A^{[0]}(\omega _8^0)+\omega _8^0A^{[1]}(\omega _8^0) =A^{[0]}(\omega _4^0)+\omega _8^0A^{[1]}(\omega _4^0) \\ &f(\omega _8^1)=A^{[0]}(\omega _8^2)+\omega _8^1A^{[1]}(\omega _8^2) =A^{[0]}(\omega _4^1)+\omega _8^1A^{[1]}(\omega _4^1) \\ &f(\omega _8^2)=A^{[0]}(\omega _8^4)+\omega _8^2A^{[1]}(\omega _8^4) =A^{[0]}(\omega _4^2)+\omega _8^2A^{[1]}(\omega _4^2) \\ &f(\omega _8^3)=A^{[0]}(\omega _8^6)+\omega _8^3A^{[1]}(\omega _8^6) =A^{[0]}(\omega _4^3)+\omega _8^3A^{[1]}(\omega _4^3) \\ &f(\omega _8^4)=A^{[0]}(\omega _8^8)+\omega _8^4A^{[1]}(\omega _8^8) =A^{[0]}(\omega _4^0)-\omega _8^0A^{[1]}(\omega _4^0) \\ &f(\omega _8^5)=A^{[0]}(\omega _8^{10})+\omega _8^5A^{[1]}(\omega _8^{10})=A^{[0]}(\omega _4^1)-\omega _8^1A^{[1]}(\omega _4^1) \\ &f(\omega _8^6)=A^{[0]}(\omega _8^{12})+\omega _8^6A^{[1]}(\omega _8^{12})=A^{[0]}(\omega _4^2)-\omega _8^2A^{[1]}(\omega _4^2) \\ &f(\omega _8^7)=A^{[0]}(\omega _8^{14})+\omega _8^7A^{[1]}(\omega _8^{14})=A^{[0]}(\omega _4^3)-\omega _8^3A^{[1]}(\omega _4^3) \end{align*}$
$\begin{align*} A^{[0]}(x)&=a_0+a_2x+a_4x^2+a_6x^3 \\ &=a_0+a_4x^2+x(a_2+a_6x^2) \end{align*}$
令$B^{[0]}(x)=a_0+a_4x,B^{[1]}(x)=a_2+a_6x$
则$A^{[0]}(x)=B^{[0]}(x^2)+xB^{[1]}(x^2)$
$\begin{align*} &A^{[0]}(\omega _4^0)=B^{[0]}(\omega _4^0)+\omega _4^0B^{[1]}(\omega _4^0)=B^{[0]}(\omega _2^0)+\omega _4^0B^{[1]}(\omega _2^0) \\ &A^{[0]}(\omega _4^1)=B^{[0]}(\omega _4^2)+\omega _4^1B^{[1]}(\omega _4^2)=B^{[0]}(\omega _2^1)+\omega _4^1B^{[1]}(\omega _2^1) \\ &A^{[0]}(\omega _4^2)=B^{[0]}(\omega _4^4)+\omega _4^2B^{[1]}(\omega _4^4)=B^{[0]}(\omega _2^0)-\omega _4^0B^{[1]}(\omega _2^0) \\ &A^{[0]}(\omega _4^3)=B^{[0]}(\omega _4^6)+\omega _4^3B^{[1]}(\omega _4^6)=B^{[0]}(\omega _2^1)-\omega _4^1B^{[1]}(\omega _2^1) \\ \end{align*}$
$\begin{align*} B^{[0]}(x)&=a_0+a_4x \\ &=a_0+xa_4 \end{align*}$
$\begin{align*} &B^{[0]}(\omega _2^0)=a_0+\omega _2^0 a_4 \\ &B^{[0]}(\omega _2^1)=a_0+\omega _2^1 a_4=a_0-\omega _2^0 a_4 \\ \end{align*}$
IFFT(快速傅里叶逆变换)
对于上面的方程组我们可以用矩阵来表示:
$$\begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \omega_8^1 & \omega_8^2 & \omega_8^3 & \omega_8^4 & \omega_8^8 & \omega_8^6 & \omega_8^7 \\ 1 & \omega_8^2 & \omega_8^4 & \omega_8^6 & \omega_8^8 & \omega_8^{10} & \omega_8^{12} & \omega_8^{14} \\ 1 & \omega_8^3 & \omega_8^6 & \omega_8^9 & \omega_8^{12} & \omega_8^{15} & \omega_8^{18} & \omega_8^{21} \\ 1 & \omega_8^4 & \omega_8^8 & \omega_8^12 & \omega_8^{16} & \omega_8^{20} & \omega_8^{24} & \omega_8^{28} \\ 1 & \omega_8^5 & \omega_8^{10} & \omega_8^{15} & \omega_8^{20} & \omega_8^{25} & \omega_8^{30} & \omega_8^{35} \\ 1 & \omega_8^6 & \omega_8^{12} & \omega_8^{18} & \omega_8^{24} & \omega_8^{30} & \omega_8^{36} & \omega_8^{42} \\ 1 & \omega_8^7 & \omega_8^{14} & \omega_8^{21} & \omega_8^{28} & \omega_8^{35} & \omega_8^{42} & \omega_8^{49} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \\ a_7 \end{bmatrix} = \begin{bmatrix} f(\omega _8^0) \\ f(\omega _8^1) \\ f(\omega _8^2) \\ f(\omega _8^3) \\ f(\omega _8^4) \\ f(\omega _8^5) \\ f(\omega _8^7) \\ f(\omega _8^7) \end{bmatrix}$$
$$\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \\ a_7 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \omega_8^1 & \omega_8^2 & \omega_8^3 & \omega_8^4 & \omega_8^8 & \omega_8^6 & \omega_8^7 \\ 1 & \omega_8^2 & \omega_8^4 & \omega_8^6 & \omega_8^8 & \omega_8^{10} & \omega_8^{12} & \omega_8^{14} \\ 1 & \omega_8^3 & \omega_8^6 & \omega_8^9 & \omega_8^{12} & \omega_8^{15} & \omega_8^{18} & \omega_8^{21} \\ 1 & \omega_8^4 & \omega_8^8 & \omega_8^12 & \omega_8^{16} & \omega_8^{20} & \omega_8^{24} & \omega_8^{28} \\ 1 & \omega_8^5 & \omega_8^{10} & \omega_8^{15} & \omega_8^{20} & \omega_8^{25} & \omega_8^{30} & \omega_8^{35} \\ 1 & \omega_8^6 & \omega_8^{12} & \omega_8^{18} & \omega_8^{24} & \omega_8^{30} & \omega_8^{36} & \omega_8^{42} \\ 1 & \omega_8^7 & \omega_8^{14} & \omega_8^{21} & \omega_8^{28} & \omega_8^{35} & \omega_8^{42} & \omega_8^{49} \end{bmatrix}^{-1} \begin{bmatrix} f(\omega _8^0) \\ f(\omega _8^1) \\ f(\omega _8^2) \\ f(\omega _8^3) \\ f(\omega _8^4) \\ f(\omega _8^5) \\ f(\omega _8^6) \\ f(\omega _8^7) \end{bmatrix} $$
看起来是不是像范德蒙德行列式。
我们只要能够得到范德蒙德矩阵的逆,一切就解决了。
事实是,普通的范德蒙德矩阵求逆很麻烦。
但,在复数领域一切都变得简单了呢。
矩阵求逆:
$$\begin{bmatrix} 1 & 1 & \cdots & 1 \\ 1 & \omega _n^1 & \cdots &\omega _n^{n-1} \\ \vdots & \vdots & & \vdots \\ 1 & \omega _n^{n-1} & \cdots & \omega _n^{(n-1)(n-1)} \end{bmatrix}^{-1} = \frac 1n \begin{bmatrix} 1 & 1 & \cdots & 1 \\ 1 & \omega _n^{-1} & \cdots &\omega _n^{-(n-1)} \\ \vdots & \vdots & & \vdots \\ 1 & \omega _n^{-(n-1)} & \cdots & \omega _n^{-(n-1)(n-1)} \end{bmatrix} $$
所以最后得到公式:
$$a(x)=f(\omega _8^0)+f(\omega _8^1)x^{1}+f(\omega _8^2)x^{2}+f(\omega _8^3)x^{3}+f(\omega _8^4)x^{4}+f(\omega _8^5)x^{5}+f(\omega _8^6)x^{6}+f(\omega _8^7)x^{7}$$
怎么感觉和最上面的$f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7$有几分相似。
只是将点,相应的变成原来的共轭复数
$\begin{align*} a(x)&=f(\omega _8^0)+f(\omega _8^1)x^{1}+f(\omega _8^2)x^{2}+f(\omega _8^3)x^{3}+f(\omega _8^4)x^{4}+f(\omega _8^5)x^{5}+f(\omega _8^6)x^{6}+f(\omega _8^7)x^{7} \\ &=f(\omega _8^0)+f(\omega _8^2)x^2+f(\omega _8^4)x^4+f(\omega _8^6)x^6+x(f(\omega _8^1)+f(\omega _8^3)x^4+f(\omega _8^5)x^4+f(\omega _8^7)x^6) \end{align*}$
$令A^{[0]}(x)=f(\omega _8^0)+f(\omega _8^2)x+f(\omega _8^4)x^2+f(\omega _8^6)x^3,A^{[1]}(x)=f(\omega _8^1)+f(\omega _8^3)x+f(\omega _8^5)x^2+f(\omega _8^7)x^3$
$则a(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)$
$\begin{align*} & a(\omega _8^0) =A^{[0]}(\omega _8^0) +\omega _8^0 A^{[1]}(\omega _8^0) =A^{[0]}(\omega _4^0)+\omega _8^0A^{[1]}(\omega _4^0) \\ & a(\omega _8^{-1})=A^{[0]}(\omega _8^{-2})+\omega _8^{-1}A^{[1]}(\omega _8^{-2})=A^{[0]}(\omega _4^{-1})+\omega _8^{-1}A^{[1]}(\omega _4^{-1}) \\ & a(\omega _8^{-2})=A^{[0]}(\omega _8^{-4})+\omega _8^{-2}A^{[1]}(\omega _8^{-4})=A^{[0]}(\omega _4^{-2})+\omega _8^{-2}A^{[1]}(\omega _4^{-2}) \\ & a(\omega _8^{-3})=A^{[0]}(\omega _8^{-6})+\omega _8^{-3}A^{[1]}(\omega _8^{-6})=A^{[0]}(\omega _4^{-3})+\omega _8^{-3}A^{[1]}(\omega _4^{-3}) \\ & a(\omega _8^{-4})=A^{[0]}(\omega _8^{-8})+\omega _8^{-4}A^{[1]}(\omega _8^{-8})=A^{[0]}(\omega _4^0)-\omega _8^0A^{[1]}(\omega _4^0) \\ & a(\omega _8^{-5})=A^{[0]}(\omega _8^{-10})+\omega _8^{-5}A^{[1]}(\omega _8^{-10})=A^{[0]}(\omega _4^{-1})-\omega _8^{-1}A^{[1]}(\omega _4^{-1}) \\ & a(\omega _8^{-6})=A^{[0]}(\omega _8^{-12})+\omega _8^{-6}A^{[1]}(\omega _8^{-12})=A^{[0]}(\omega _4^{-2})-\omega _8^{-2}A^{[1]}(\omega _4^{-2}) \\ & a(\omega _8^{-7})=A^{[0]}(\omega _8^{-14})+\omega _8^{-7}A^{[1]}(\omega _8^{-14})=A^{[0]}(\omega _4^{-3})-\omega _8^{-3}A^{[1]}(\omega _4^{-3}) \end{align*}$
$\begin{align*} A^{[0]}(x)&=f(\omega _8^0)+f(\omega _8^2)x+f(\omega _8^4)x^2+f(\omega _8^6)x^3 \\ &=f(\omega _8^0)+f(\omega _8^4)x^2+x(f(\omega _8^2)+f(\omega _8^6)x^2) \end{align*}$
令$B^{[0]}(x)=f(\omega _8^0)+f(\omega _8^4)x,B^{[1]}(x)=f(\omega _8^2)+f(\omega _8^6)x$
则$A^{[0]}(x)=B^{[0]}(x^2)+xB^{[1]}(x^2)$
$\begin{align*} &A^{[0]}(\omega _4^0) =B^{[0]}(\omega _4^0)+\omega _4^0B^{[1]}(\omega _4^0) =B^{[0]}(\omega _2^0)+\omega _4^0B^{[1]}(\omega _2^0) \\ &A^{[0]}(\omega _4^{-1})=B^{[0]}(\omega _4^{-2})+\omega _4^{-1}B^{[1]}(\omega _4^{-2})=B^{[0]}(\omega _2^{-1})+\omega _4^{-1}B^{[1]}(\omega _2^{-1}) \\ &A^{[0]}(\omega _4^{-2})=B^{[0]}(\omega _4^{-4})+\omega _4^{-2}B^{[1]}(\omega _4^{-4})=B^{[0]}(\omega _2^0)-\omega _4^0B^{[1]}(\omega _2^0) \\ &A^{[0]}(\omega _4^{-3})=B^{[0]}(\omega _4^{-6})+\omega _4^{-3}B^{[1]}(\omega _4^{-6})=B^{[0]}(\omega _2^{-1})-\omega _4^{-1}B^{[1]}(\omega _2^{-1}) \\ \end{align*}$
$\begin{align*} B^{[0]}(x)&=f(\omega _8^0)+f(\omega _8^4)x \\ &=f(\omega _8^0)+xf(\omega _8^4) \end{align*}$
$\begin{align*} &B^{[0]}(\omega _2^0)=a_0+\omega _2^0 a_4 \\ &B^{[0]}(\omega _2^{-1})=a_0+\omega _2^{-1} a_4=a_0-\omega _2^0 a_4 \\ \end{align*}$
相信给出一张图片,你就能明白啦!!!
注意:处理的长度只能是2的次幂,所以对于多项式相乘,应该将长度n变成:大于等于n的最小的2的次幂,再乘以2。以保证不会溢出。
记得除以n。
代码如下:
void FFT(complex *a, int n, int inv) //inv=1 FFT inv=-1 IFFT
{
if (n == 1)
return;
int mid = n / 2;
for (int i = 0; i < mid; i++)
{
rev[i] = a[i*2];
rev[i + mid] = a[i * 2 + 1];
}
for (int i = 0; i < n; i++)
{
a[i] = rev[i];
}
FFT(a, mid, inv);
FFT(a + mid, mid, inv);
for (int i = 0; i < mid; i++)
{
complex w(cos(2 * pi * i / n), inv * sin(2 * pi * i / n));
complex l = a[i];
complex r = w * a[i+mid];
a[i] = l+r;
a[i + mid] = l-r;
}
} 优化
上面的代码层层递归,还是很耗时的,如果我们一开始就将各位数放到他们应该去的位置,就可以快很多了。
$$\begin{matrix} a_0 & a_1 & a_2 & a_3 & a_4 & a_5 & a_6 & a_7 \\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow &\downarrow \\ 000 & 001 & 010 & 011 & 100 & 101 & 110 & 111\\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow &\downarrow \\ 位反转 & 位反转 & 位反转 & 位反转 & 位反转 & 位反转 & 位反转 & 位反转 & \\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow &\downarrow \\ 000 & 100 & 010 & 110 & 001 & 101 & 011 & 111 \\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow &\downarrow \\ a_0 & a_4 & a_2 & a_6 & a_1 & a_5 & a_3 & a_7 \end{matrix}$$
代码如下:
void FFT(complex* a, int n, int inv)
{
int bit = 0;
while ((1 << bit) < n) bit++;
for (int i = 0; i < n; i++)
{
rev[i] = a[(rev32bit(i) >> (32 - (bit)))];
}
for (int i = 0; i < n; i++)
{
a[i] = rev[i];
}
for (int mid = 1; mid < n; mid *= 2)
{
complex w(cos(pi / mid), inv * sin(pi / mid));
for (int i = 0; i < n; i += mid * 2)
{
complex temp = 1;
for (int j = 0; j < mid; j++, temp *= w)
{
//complex w(cos(pi * j / mid), inv * sin(pi * j / mid));
complex l = a[i + j];
complex r = temp * a[i + j + mid];
a[i + j] = l + r;
a[i + j + mid] = l - r;
}
}
}
} 32位反转算法代码如下:
unsigned int rev32bit(unsigned int x)
{
x = ((x & 0x55555555) << 1) | ((x & 0xaaaaaaaa) >> 1);
x = ((x & 0x33333333) << 2) | ((x & 0xcccccccc) >> 2);
x = ((x & 0x0f0f0f0f) << 4) | ((x & 0xf0f0f0f0) >> 4);
x = ((x & 0x00ff00ff) << 8) | ((x & 0xff00ff00) >> 8);
x = ((x & 0x0000ffff) << 16) | ((x & 0xffff0000) >> 16);
return x;
}注意:上面的代码不能直接用,例如4的位反转为0x20000000。即00000000 00000000 00000000 00000100b反转后为00100000 00000000 00000000 00000000b,我们需要右位移29(32-$\log_2^{长度}$)位,得到0x0001,即为1。
扩展
求解第一个大于等于n的2的次幂
代码如下
int FGE2(int n)
{
int temp = n - 1;
temp |= temp >> 1;
temp |= temp >> 2;
temp |= temp >> 4;
temp |= temp >> 8;
temp |= temp >> 16;
//temp |= temp >> 32; //如果类型是long long
return temp + 1;
}大数FFT
我们以大数$abcdef$为例,$f(x)=f+ex+dx^2+cx^3+bx^4+ax^5+0x^6+0x^7$,则$f(10)=abcdef$
我们以$21\times 34$为例:
$$f(x)=1+2x+0x^2+0x^3$$
$$g(x)=4+3x+0x^2+0x^3$$
$$h(x)=f(x)g(x)=4+11x+6x^2+0x^3$$
$$(1+2x)(4+3x)=4+11x+6x^2$$
$$x=10,~21\times 34=4+110+600=714$$
实际中,将多项式系数进位就可以得到。例如将11进位,将1加到6,得到4,1,7。
例题
HDU 1402
#include
#include
#include
#include
using namespace std;
double pi = acos(-1);
complex A[131072], B[131072];
int answer[131072];
char sa[50000], sb[50000];
unsigned int rev32bit(unsigned int x)
{
x = ((x & 0x55555555) << 1) | ((x & 0xaaaaaaaa) >> 1);
x = ((x & 0x33333333) << 2) | ((x & 0xcccccccc) >> 2);
x = ((x & 0x0f0f0f0f) << 4) | ((x & 0xf0f0f0f0) >> 4);
x = ((x & 0x00ff00ff) << 8) | ((x & 0xff00ff00) >> 8);
x = ((x & 0x0000ffff) << 16) | ((x & 0xffff0000) >> 16);
return x;
}
void FFT(complex* a, int n, int inv)
{
int bit = 0;
while ((1 << bit) < n) bit++;
for (int i = 0; i < n; i++)
{
int temp = rev32bit(i) >> (32 - (bit));
if (i < temp)
swap(a[i], a[temp]);
}
for (int mid = 1; mid < n; mid *= 2)
{
complex w(cos(pi / mid), inv * sin(pi / mid));
for (int i = 0; i < n; i += mid * 2)
{
complex temp = 1;
for (int j = 0; j < mid; j++, temp *= w)
{
//complex w(cos(pi * j / mid), inv * sin(pi * j / mid));
complex l = a[i + j];
complex r = temp * a[i + j + mid];
a[i + j] = l + r;
a[i + j + mid] = l - r;
}
}
}
}
int FGE2(int n)
{
int temp = n - 1;
temp |= temp >> 1;
temp |= temp >> 2;
temp |= temp >> 4;
temp |= temp >> 8;
return temp + 1;
}
int main(int argc, char* argv[])
{
while (~scanf("%s%s", sa, sb))
{
int len1 = strlen(sa);
int len2 = strlen(sb);
int len = FGE2(max(len1, len2)) * 2;
for (int i = 0; i < len1; i++)
A[i] = sa[len1 - i - 1] - '0';
for (int i = len1; i < len; i++)
A[i] = 0;
for (int i = 0; i < len2; i++)
B[i] = sb[len2 - i - 1] - '0';
for (int i = len2; i < len; i++)
B[i] = 0;
FFT(A, len, 1);
FFT(B, len, 1);
for (int i = 0; i < len; i++)
{
A[i] = A[i] * B[i];
}
FFT(A, len, -1);
for (int i = 0; i < len; i++)
{
answer[i] = (int)(A[i].real() / len + 0.5);
}
for (int i = 0; i < len - 1; i++)
{
answer[i + 1] += answer[i] / 10;
answer[i] %= 10;
}
int index;
for (index = len - 1; index > 0; index--)
{
if (answer[index] != 0)
break;
}
for (int i = index; i >= 0; i--)
{
printf("%d", answer[i]);
}
printf("\n");
}
return 0;
} ![]()
洛谷 P1919
只需要将数组大小改成2097152和1000000即可。