对于有趋势的季节需求,我们这里介绍一个常用的方法,准确度不是最高,但相对简单易行。
我们先看一下季节性和周期性的区别。周期性是时间序列呈现出波浪形起伏,上下起伏,一般由商业和经济活动引起。它不同于趋势变 动,不是朝着单一方向的持续运动,而是涨落相间的交替波动;它也不同于季节变动,季节变动有比较固定的规律,而循环波动则无固定规律[1]。可以说,周期性和季节性都有波峰波谷,前者缺乏规律性,可预见性低;后者规律性强,容易预见。
提到季节性,人们想到的就是一年四季。这没错,不过季节性不一定非得要一年,一天、一周、一个月,甚至一个小时,一分钟,都可以有季节性。比如你开个餐馆,早饭、午饭和晚饭的需求量不同,对店面人工的需要早晨少,中午和晚上多,这是一天的季节性。同样,作为餐馆,周五、周六的生意一般最忙,而周二一般最清闲(这也在美国,很多餐馆周二有特价的原因),这是一周的季节性。电商也类似,在一周里跟餐馆的周期性正好相反:周末的时候,小姑娘们都出去逛街吃饭,没多少人在网购;周二的时候,大家都窝在家里不出去,你会发现网购的量会更高——我在分析一个电商的业务时,看到类似的模式。
如果是单纯的季节性,季度与季度之间没有趋势的话,我们可以求出每个季节跟平均值比较,用来预测下一年各季的需求。就如下面的例子中,上年四个季度的平均值已知(2500个),根据每个季度的需求,就可求出每个季度对应的季度系数。
季度 需求 季节性系数
春季 2000 2000/2500 = 0.8
夏季 3500 3500/2500 = 1.4
秋季 3000 3000/2500 = 1.2
冬季 1500 1500/2500 = 0.6
假定这个产品每年以30%的趋势增长,那么下一年的总预测就是13000,每个季度的平均预测是13000/4=3250,相应地可以预测每个季度的需求:
季度 预测
春季 3250 * 0.8 = 2600
夏季 3250 * 1.4 = 4550
秋季 3250 * 1.2 = 3900
冬季 3250 * 0.6 = 1950
这其实也不难。有趣的是,读因特尔前CEO格鲁夫的书,其中提到,照相机用的胶卷就是这样的季节性产品,即便在每年的需求量变化不大的情况下,在匈牙利的计划经济时代,那些国营企业还是没法生产出合适的量来(格鲁夫是匈牙利裔)。计划经济之“计划”性,可见一斑。
我们下面看一下季节性、趋势并存的情况[2]。如图 1,这个产品的销量具有季节性,每四期是一个周期;同时,需求也呈现出趋势。我们的任务是预测第13到16期的需求。这里的“期”可以理解为季度、月度、周、天等任何时间单元(案例中的期其实是季度)。
图1:季节性和趋势并存的时间序列
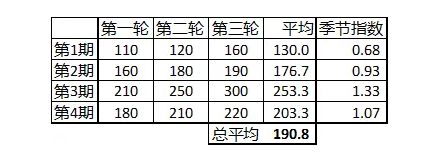
我们先求每一期的季节指数。如表 1,鉴于季节性每4期循环一次,我们把12期的数据分为三轮(可以理解为3年),求出每期的三轮平均值。每期的平均值与12期的总平均值相比,就得到该期的季节指数。比如第二期的平均值为176.7,12期的总平均为190.8,两者相除,得到第二期的季节指数为0.93,意味着第二期是平均需求的93%(低于100%的话,可以理解为淡季;高于100%,可以理解为旺季)。
表1:季节指数的计算
接着我们求趋势。在求趋势前,我们先得去季节化,也就是每期的需求除以季节指数。如表 2,第④列就是假定没有季节性时,每期的需求。围绕第①和第④列的数据,我们来运行线性回归(具体的做法后文会详细谈到),得出线性回归方程为需求预测=152.44+5.91*期数。这里的5.91就是我们说的“趋势”,也就是,每期比上期增加5.91个。这样,我们就能够求出不包含季节性的线性预测,见第⑤列。比如第13期的线性预测等于152.44+5.91*13=229.27,四舍五入为229。
最后一步呢,就是把季节指数反算进去,求得季节性调整后的预测,亦即我们最终需要的预测。这是拿线性预测(第⑤列)跟季节指数(第②列)相乘。比如第14期的最终预测就是235*0.93=218。
第①列的实际值和第⑥列的预测值相减,就得到第⑦列的预测误差。围绕该误差,我们可以设置一定的安全库存,来应对预测的不准确,也是需求的不确定性,计算的详情见第二章“量化不确定性,设立安全库存”部分。
表2:预测趋势和季节性并存的情况
【实践者问】这里介绍的季节性+趋势的模型,跟霍尔特-温特模型有什么区别?
【刘宝红答】这里的模型简单,但能够优化的地方很有限,比如趋势和季节性参数都没法调整,所以模型比较“僵硬”,预测的准确度也受影响。在霍尔特-温特模型中,我们可以调整三个平滑参数,提高模型的拟合度,也提高预测的准确度。
霍尔特-温特模型就像个“三节棍”,灵活是灵活,但很难使——如果使得好,那可不得了。一般人还是用“两节棍”或者简单的棍子得了。
看到这里,有些人或许或问,现在的产品生命周期都这么短,哪能有两年、三年、四年的需求历史,让我们来求这些季节指数、趋势,预测未来的需求?从具体的成品来说,这或许没错;但对半成品、原材料、产能来说,却未必。比如你是卖热饮的,季节性非常明显的产品(天气冷了需求量大,热了需求量小),热饮的包装就如快时尚,更新频次相当高;但热饮本身(半成品)和原材料的变化就没那么大,生产线和工艺也是年复一年差不多,我们在半成品、原材料、产能层面还是可以做类似的预测,指导整个供应链更加有序地响应。
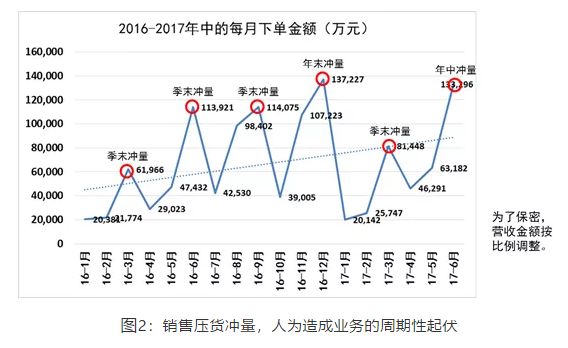
再比如在有些行业,压货行为非常普遍,人为制造了季节性。比如在图 2中,某工业品企业的销售习惯性地向渠道压货,1月份没什么生意,2月份也没多少,3月份是季末,考核时间到了,就拼命向渠道压货,需求大增;季度考核完了,4月份就没多少生意,5月份稍微增长点,6月份是季末和半年考核,销售冲量就更厉害。就这样,三个月一个周期,业务上下起伏,多年来都如此。除了季节性,该企业的业务整体上一直在增长,是典型的季节性+趋势。
图2:销售压货冲量,人为造成业务的周期性起伏
销售的压货行为,后面有深刻的绩效考核、组织行为和产品竞争力等原因,这里不细讲[3]。作为供应链,我们除了抱怨,还可以用这里讲的方法,预测销售的压货行为,尽量来驱动供应链有序应对。当然,我说这些,并不是说“金有狼牙棒,宋有天灵盖”,提倡供应链逆来顺受:当产品的竞争力有限,绩效考核短期难以改变的时候,相同的外界约束下,计划和供应链还是有可作为的;只要做了我们可作为的,我们就可以做得比以前好,比同行好,这就是竞争优势。
我们再回到图 1的例子。这是个完美的季节性带趋势的例子,我们可以相当准确地预测出来(从第⑦列的预测误差即可看出)。实践中,我们很少会有这样的完美情况。我们的应对方案还是一样:其一,尽量作准:寻找更合适的预测方法,比如霍尔特-温特模型,通过优化各参数,来尽量提高预测准确度;其二,尽快纠偏:有了一点实际销售数据,要尽早分析,与原来的预测比较,与历史数据比较,再结合市场、销售、产品管理等的职业判断,尽快调整预测。这样做,至少可以避免大错特错。
此外,不管是季节性,周期性,还是趋势,都是相对特定的供应链响应周期、响应能力而言。当供应链的响应周期很短,响应能力无限的时候,对这些变动性的预测就不那么重要。比如这是个前置仓,或者门店,补货周期就那么几个小时或几天,反映不出来多少季节性、趋势,你也就用不着采取复杂的模型来预测——移动平均法,简单指数平滑法,甚至卖一补一的“幼稚预测”,八成就能够很好应对。但是,如果你要规划前置仓、门店的规模,决定是否扩容的话,那可是长周期行为,我们得预测未来几个季度甚至几年的需求,这时候,季节性、趋势等更复杂的情形预测就更必要。产线的产能、供应商的产能、长周期物料的备料也是同理。