串的模式匹配问题的相关算法
概念:
设有两个串S和P,如果P是S的子串,则将查找P在S中出现的位置的操作过程称为模式匹配,称S为正文(text),称P为模式(pattern)。
求子串位置的定位操作:例如:S=”ABCABDABCDABC”,P=”ABCD”,我们把P在S中首次出现的位置作为子串P在S中的位置。
算法一:蛮力法
1.1 匹配过程(如图所示)
1.2 算法的基本思想
从正文s的第一个字符起和模式的第一个字符比较,若相等,则继续逐个比较后续字符,否则从正文的第二个字符起重新与模式的字符比较,以此类推,直至模式t中的每个字符依次和主串s中的一个连续字符序列相等,则称匹配成功,返回与模式t中的第一个字符相等的字符在正文s中的索引,否则匹配不成功,返回-1。
1.3 伪代码描述
算法 BruteForceStringMatch(T[0...n-1], P[0...m-1])
//输入:一个n个字符的数组T[0...n-1]代表文本
// 一个m个字符的数组P[0...m-1]代表模式
//输出:如果查找成功,返回文本中与子串相匹配的字符序列的第一个字符的索引;
// 如果查找失败,返回-1。
for n ← 0 to n-m do
j ← 0
while j < m and T[i+j] = P[j] do
j ← j + 1
if j = m
return i
return -1
最坏时间复杂度:![]()
1.4 JAVA代码实现
// 蛮力字符串匹配
public static int bruteForceStringMatch(String text, String pattern) {
char[] textCharArray = text.toCharArray();
char[] patternCharArray = pattern.toCharArray();
for (int i = 0; i <= textCharArray.length - patternCharArray.length; i++) {
int j = 0;
while(j < patternCharArray.length && textCharArray[i+j] == patternCharArray[j]) {
j++;
}
if(j == patternCharArray.length) {
return i;
}
}
return -1;
}算法二:KMP算法
2.1 匹配过程
我们考虑这样一个问题:主串为”LMLMNA”,模式串为”LMN”,我们可不可以实现这样的匹配过程:
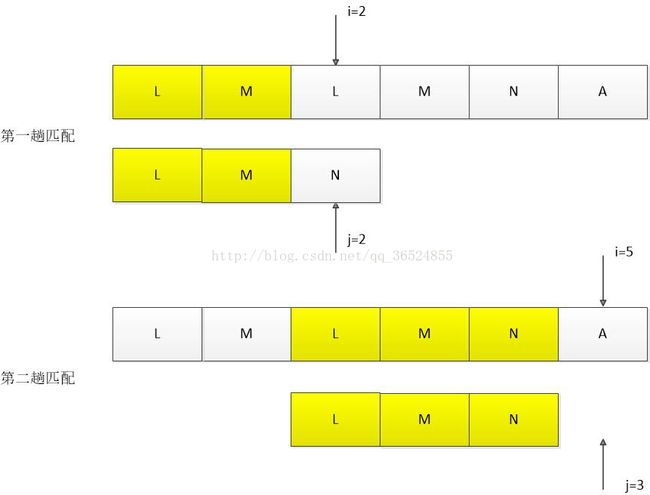
第一趟匹配时,i=0,j=0开始,直至i=2时,T[i]与P[j]不相等。
按照蛮力算法操作的话,i应当后移一位,即i=1,j=0重新开始匹配。可是,这样的做法显然做了一部分无用功。
因为模式串本身是不重复的,与之部分匹配的,我是不是可以直接跳过?也就是跳过i=1,j=0的过程,直接跳过已经匹配的字符序列,答案是肯定的。
即直接从i=2,j=0开始(蛮力法的第二趟匹配i=1,j=0开始),即在第一趟匹配的基础上,i指针不改变,将模式串右移2位。
那么,2是什么含义呢?即已匹配的字符数。
对于不重复的模式串,当出现部分匹配的情况时,我们不改变i指针的位置,将模式串右移一定位数(与已匹配的字符数等长的位数)。
对于部分重复的模式串,我们应该怎么做呢?怎么做才可以将模式串右移一定位数,并且保证不会漏掉可能的匹配,也不重复不必要的匹配匹配过程呢?
比如,主串为”ABCDABCDABDABCDABE”,模式串为”ABCDABD”,实现这样的匹配:
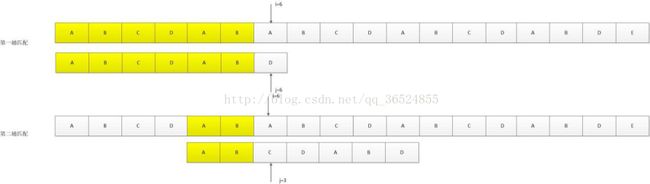
第一趟匹配,i=0,j=0开始,直至i=6。
第二趟匹配,i=6,j=3开始。也就是说,i指针保持不变,模式串右移4位。那么,这个4是怎么来的呢?已匹配的字符数为6,减去模式串中重复的最大长度2,即为4;(减去2的目的是保证不漏掉可能的匹配!)
注意:认真体会以上过程,帮助编写代码,理解代码。
2.2 KMP算法的核心思想
不改变主串指针位置,移动模式串,移动的位数=已匹配的字符数-部分匹配值。
2.3 自身重复表
为了保证不漏掉可能的匹配,也不重复不必要的匹配过程,我们针对模式串建立对应的部分匹配表。也就是说,我们需要依次计算出模式串中每一个字符的部分匹配值。问题来了,怎么计算呢?回到初衷,所谓“部分匹配值”,也就是最长的重复长度。
在这里,我们引入前缀、后缀的概念。
前缀:除最后一个字符以外,字符串的所有头部组合。
后缀:除第一个字符以外,字符串的所有尾部组合。
部分匹配值:前缀和后缀的最长共有元素的长度。(也就是,前缀和后缀的交集里面最长的元素的长度,即为自身匹配值。)
注意:是共有元素的长度(默念三百遍长度!!!),而不是共有元素的个数
举例:模式串“ABCDABD”
| 模式串解析 |
前缀 |
后缀 |
部分匹配值 |
| “A” |
∅ |
∅ |
0 |
| “AB” |
{“A”} |
{“B”} |
0 |
| “ABC” |
{“A”,“AB”} |
{“C”,“BC”} |
0 |
| “ABCD” |
{“A”,“AB”,“ABC”} |
{“D”,“CD”,“BCD”} |
0 |
| “ABCDA” |
{“A”,“AB”,“ABC”,“ABCD”} |
{“A”,“DA”,“CDA”,“BCDA”} |
1 |
| “ABCDAB” |
{“A”,“AB”,“ABC”,“ABCD”,“ABCDA”} |
{“B”,“AB”,“DAB”,“CDAB”,“BCDAB”} |
2 |
| “ABCDABD” |
{“A”,“AB”,“ABC”,“ABCD”,“ABCDA”,“ABCDAB”} |
{“D”,“BD”,“ABD”,“DABD”,“CDABD”,“BCDABD”} |
0 |
2.3 JAVA代码实现
// KMP算法
public static int KMPStringMatch(String text, String pattern) {
int[] next = getNext(pattern);
for (int i = 0, j = 0; i <= text.length() - pattern.length(); i++) {
while(j > 0 && pattern.charAt(j) != text.charAt(i)) {
j = next[j-1];
}
if(pattern.charAt(j) == text.charAt(i)) {
j++;
}
if(j == pattern.length()) {
return i - j + 1;
}
}
return -1;
}
// 生成部分匹配表
public static int[] getNext(String str) {
int[] next = new int[str.length()];
next[0] = 0;
for (int i = 1, j = 0; i < next.length; i++) {
while(j > 0 && str.charAt(i) != str.charAt(j)) {
j = next[j-1];
}
if(str.charAt(i) == str.charAt(j)) {
j++;
}
next[i] = j;
}
return next;
}2.4 算法评价
时间复杂度:![]()
与蛮力法比较,以开辟一个大小为m数组空间为代价,提高时间复杂度!证明了时间与空间,二者不可兼。
推荐链接:(参考资料)
http://blog.csdn.net/v_july_v/article/details/7041827
http://blog.csdn.net/maotianwang/article/details/34466483
http://blog.csdn.net/qq_26411333/article/details/51622537
