TensorFlow学习——张量运算

张量运算

加减乘除四则运算

算术操作	描述
tf.add(x,y)	将x和y逐元素相加
tf.subtract(x,y)	将x和y逐元素相减
tf.multiply(x,y)	将x和y逐元素相乘
tf.divide(x,y)	将x和y逐元素相除
tf.math.mod(x,y)	将x逐元素求余

逐元素操作是指把x中的每一个元素与y中的每一个元素逐个地进行运算，但是实际上是可以用数学符号+-/*%去代替的。例：

# 逐元素相加
a = tf.constant([1, 2, 3])
b = tf.constant([4, 5, 6])
c = tf.add(a, b)
print(c)

# 逐元素相减
d = tf.subtract(b, a)
print(d)

# 逐元素相乘
e = tf.multiply(a, b)
print(e)

# 逐元素相除
f = tf.divide(a, b)
print(f)

# 逐元素求余
g = tf.math.mod(a, b)
print(g)

print(a - b)
print(a * b)
print(a / b)
print(a + b)
print(a % b)
print(a // b)

需要注意的是/运算虽然除数与被除数的元素类型都是int32的，但是得到的结果却是float64，如果想要得到的运算是整除运算可以用//来进行整除运算。

幂指对数运算

算术运算	运算描述
tf.pow(x,y)	对x求y的幂次方
tf.square(x)	对x逐个元素求二次方
tf.sqrt(x)	对x逐元素开平方根
tf.exp(x)	计算e的x次方
tf.math.log(x)	计算自然对数，底数为e

a = tf.reshape(tf.range(6), shape=(2, 3))
print(tf.pow(a, 2))
print(a ** 2)
print(tf.square(a))

print(tf.sqrt(tf.cast(a, dtype=tf.float32)))
print(tf.cast(a, dtype=tf.float32) ** (1 / 2))

print(tf.math.log(tf.cast(a, dtype=tf.float32)))
print(tf.exp(tf.cast(a,dtype=tf.float32)))

如上所示，对张量每个元素求平方或平方根也是可以用**这种数学符号的，但是需要注意的是在计算自然对数与求平方根时，张量的类型需要是浮点型，使用整型会报错。

由于TensorFlow中只有以e为底的自然对数，没有提供其它数值为底的对数运算函数，但是我们可以用数学运算中的换底公式来计算其它底数的对数，$lo{g}_{a}b=\frac{lo{g}_{c}b}{lo{g}_{c}a}$

其它运算

三角函数与反三角函数运算

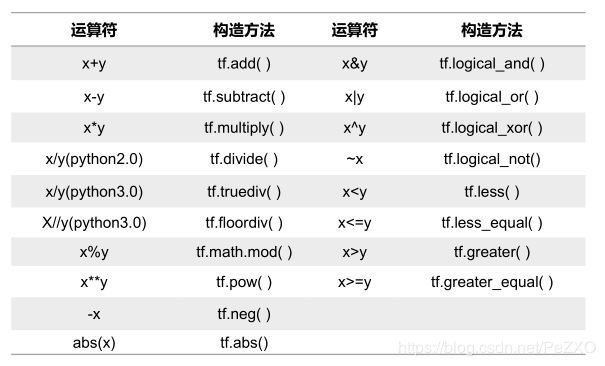
重载运算符

广播机制（broadcaing）

例如，一维张量与二维向量相加时，一维向量中每个元素会与二维向量中最小的那个维度中的每个元素逐个相加。

需要注意的是两个张量最后一个维度的长度必须相等。

a = tf.constant([1, 2, 3])
b = tf.reshape(tf.range(12), shape=(4, 3))
print(a + b)

一维张量和三维张量的相加也与一维张量与二维张量相加的情况相同，都是最小维度之间各个元素相加。

数字+N维张量时，这个数字也会与张量的各个元素进行相加。

张量乘法

元素乘法：tf.multiply()，可以用*运算符代替，

向量乘法：tf.matmul()，可以用@运算符代替。向量乘法采用的乘法是线性代数中的矩阵之间相乘的运算。

a = tf.reshape(tf.range(6), shape=(2,3))
b = tf.reshape(tf.range(6), shape=(3,2))
print(a@b)

对于多维张量中的三维张量与三维常量普通乘法之间的运算遵循的原则是最后两位做向量乘法，高维采用广播机制（其实四维也是）。

一图说明：

张量数据统计函数

求和函数：tf.reduce_sum()，这个函数可以设定axis参数，以此来指定对某个维度进行求和，如果不设置，就会默认对所有元素进行求和运算。

a = tf.reshape(tf.range(12),shape=(2,2,3))
print(tf.reduce_sum(a))
print(tf.reduce_sum(a,axis=2))

与之相似的还有tf.reduce_mean()求均值函数，tf.max()求最大值函数，tf.min()求最小值函数，tf.argmax()求最大值索引，tf.argmin()求最小值索引。

需要注意的是求均值函数在张量类型为整型时，所得到的均值张量也是整型。