2020杭电暑期多校02 10 - Lead of Wisdom (HDU6772) 常数坑

20200725005909

2020杭电暑期多校02 10 - Lead of Wisdom (HDU6772) 常数坑

如果一直 TLE，就看第三章。

一、题意

物品可能的种类有 $k$ 种，编号为 $[1,k]$。

有 $n$ 件物品，第 $i$ 件物品属于某一种类 $t_i$ 并拥有四个非负整数的属性值 $a_i,b_i,c_i,d_i$。

现在，我们对每一种类最多取其中一件物品，最终得到所取出物品的集合 $S$（元素为所取物品的编号），则我们的总收获为
$$DMG=(100+\sum _{i\in S}{a}_i)(100+\sum _{i\in S}{b}_i)(100+\sum _{i\in S}{c}_i)(100+\sum _{i\in S}{d}_i)$$
求能得到的最大收获。

$样例数T\le 10;$

$n,k\le 50;1\le t_i\le k;0\le a_i,b_i,c_i,d_i\le 100;$

注意，样例输入隐含了重要题意信息：

1
6 4
1 17 25 10 0
2 0 0 25 14
4 17 0 21 0
1 5 22 0 10
2 0 16 20 0
4 37 0 0 0

二、题解

发现数据较小，先考虑暴力搜索，下面证明其可行性。

首先，既然属性值非负，那么我们对每个种类都应取一件物品，除非这一种类不含任何物品。

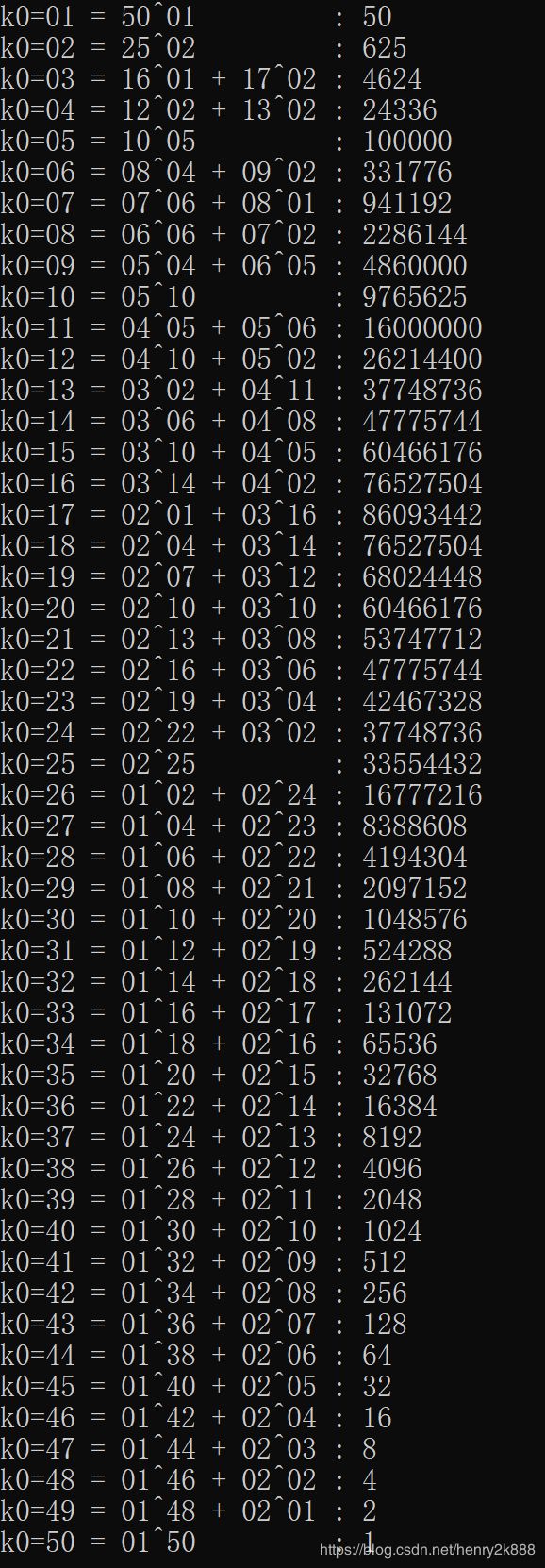
当总共有 $k=k_0$ 种种类时，最大复杂度是多少？设 第 $i$ 种有 $cn{t}_i$ 件物品，则复杂度为 ${\Pi }_{i=1}^{k}cn{t}_i$。显然，当每种物品数量比较均衡时上述乘积达到最大。具体来说，由于每组平均有 $\frac{n}{k}$ 件物品，我们可令含有 $\lceil \frac{n}{k}\rceil$ 件物品的种类数为 $n\mathrm{m}\mathrm{o}\mathrm{d}k$，其余种类含有 $\lfloor \frac{n}{k}\rfloor$ 件物品，则最为平均。

然后我们再对 $k_0$ 取 $[1,50]$ 各值，发现当种类数 $k_0=17$ 时复杂度最大：

则暴力搜索的单样例复杂度约 $8.6\ast 10^7$，总复杂度达 $8.6\ast 10^8$，本地电脑实测可以过。

然而，交上去却TLE，对此我们进行了各类优化：递归改为用栈循环并进一步改成手写栈、减少 long long 运算（因为在最后一步相乘得答案前，加法不会爆 int）都没用。

三、本题的坑

仔细研究样例，会发现虽然输入 $k=4$，但实际物品种类只有三种，即允许有种类是不含任何物品的（第二章也稍稍提到了）。再看官方题解和各博客，发现多次提及 $cn{t}_i=0$ 的种类应跳过。这便引出了此题又一个巨大的常数……

以种类数为 $17$ 为例，此时最坏情况有 $16$ 个种类含三件物品、$1$ 个种类含两件物品。然而当输入 $k=50$ 时，就会有 $33$ 个空的种类（不含任何物品）！把dfs过程视为一棵树，我们本应递归 $17$ 层访问 $8.6\ast 10^8$ 个叶子节点（可能情况），但如果这 $33$ 个空种类（空递归层）造成的树链被加在了每个叶子的下方（这是最坏情况，当然这些链也可能加在中间层），就会增加 $8.6\ast 10^8\ast 33$ 次递归调用（树上节点）！这只是举例，最坏情况也不一定发生在 $17$ 种种类时呢？没有进一步计算探究了。

解决方法很简单，每组样例只需要在dfs前花费 $O(50)$ 遍历一遍所有种类，用链表记录非空种类，后续递归只关注链表上的种类即可。

四、AC代码

#include
#include
#include
#define ll long long

int t[55], a1[55], b1[55], c1[55], d1[55];
std::vector<int> items[55];  // items[i] stores the (id of) items of the i-th type.
int next_type[55];
int last_type;

ll max_ans;

void dfs(int ind , int a , int b , int c , int d){
    if(ind==0){
        max_ans = std::max( max_ans , 1LL*a*b*c*d );
        return;
    }
    for(int i=0 ; i<items[ind].size() ; ++i){
        int j=items[ind][i];
        dfs(next_type[ind] , a+a1[j] , b+b1[j] , c+c1[j] , d+d1[j]);
    }
}

int main(){
    int T;
    scanf("%d" , &T);
    while(T--){
        int n,k;
        scanf("%d%d" , &n , &k);
        for(int i=1 ; i<=k ; ++i) items[i].clear();
        for(int i=1 ; i<=n ; ++i){
            scanf("%d%d%d%d%d" , &t[i] , &a1[i] , &b1[i] , &c1[i] , &d1[i]);
            items[t[i]].push_back(i);
        }

        last_type=51;
        for(int i=k ; i>=1 ; --i){
            if(items[i].size()==0) continue;
            next_type[last_type]=i;
            last_type = i;
        }
        next_type[last_type]=0;

        max_ans=0;
        dfs(next_type[51] , 100 , 100 , 100 , 100);
        printf("%lld\n" , max_ans);
    }
    return 0;
}