BF算法和KMP算法详解
目录
串的模式匹配算法:
算法目的
算法种类
<1> BF算法(穷举法)
<2>KMP算法
BF算法
算法的思路
具体过程
子串位置的计算
代码实现
时间复杂度
KMP算法
求解next的方法
求next[j+1]
使用next数组来实现过程
代码实现
next 数组的优化
代码实现
串的模式匹配算法:
算法目的:
确定主串中所含子串(模式串)第一次出现的位置(定位)。
算法种类:
<1> BF算法(穷举法)
<2>KMP算法
特点:速度快
BF算法
Brute-Force简称为BF算法,亦称简单匹配算法,采用穷举法(将结果一一列出来的方法)的思路。
下面我们举个例子来理解一下:
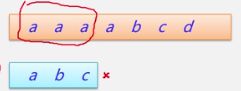
主串S (正文串): a a a a b c d
子串T (模式串): a b c
它的过程是这样的:
1.先比较前三个
发现不匹配
2.再比较后面的三个
发现还是不匹配
3.再继续比较后面的三个
发现还是不匹配
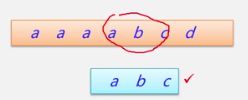
4.再继续比较
匹配成功
算法的思路:
从S的每一个字符开始依次与T的字符进行匹配。
理解了之后,我们来看一下这个算法的具体执行过程。
我们学了串的顺序存储法之后,知道了串是用一维数组来存的,为了方便,数组下标为0的位置不存元素,从下标为1的位置开始存,所以 i 和 j 的初值都是1(i 和 j 均表示下标)。
具体过程:
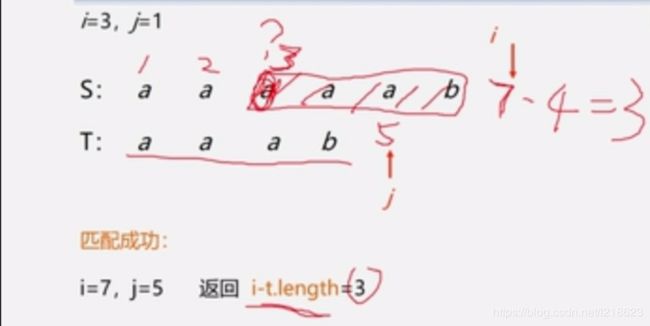
i=1,j=1
发现相同,所以让 i++,j++,得:
i=2,j=2
发现相同,所以让 i++,j++,得:
i=3,j=3
发现相同,所以让 i++,j++,得:
i=4,j=4
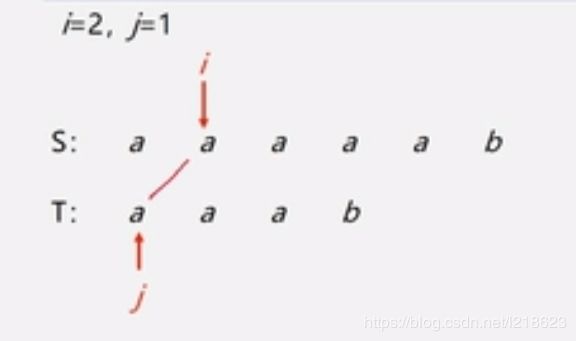
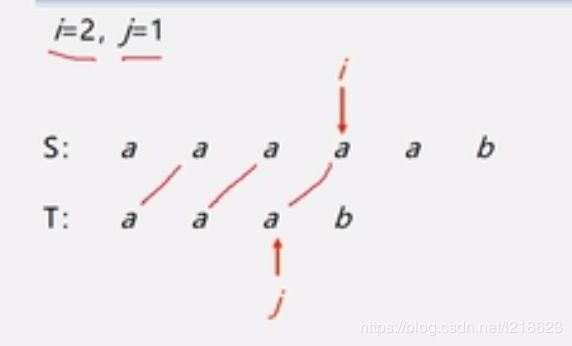
发现不相同,所以让 i 回溯(公式:i-j+2),即 i=2,让 j 回到最开始的位置,即 j=1,得:
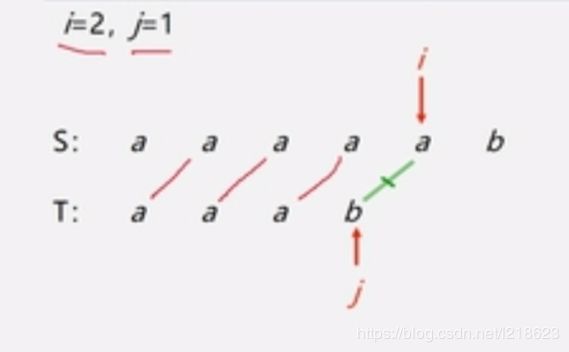
i=2,j=1
重复以上的比较过程:
直到这样,发现不相同,所以再让 i 回溯(公式:i-j+2),即 i=3,让 j 回到最开始的位置,即 j=1,得:
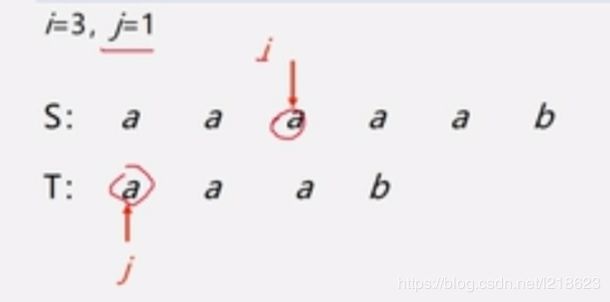
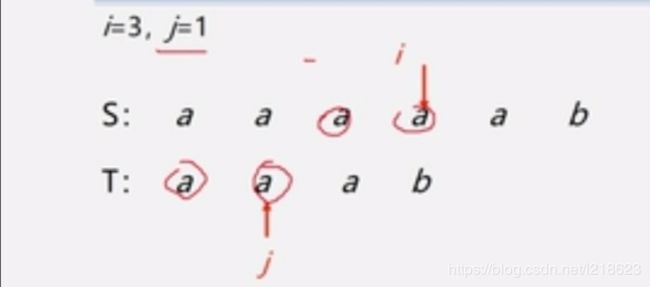
i=3,j=1
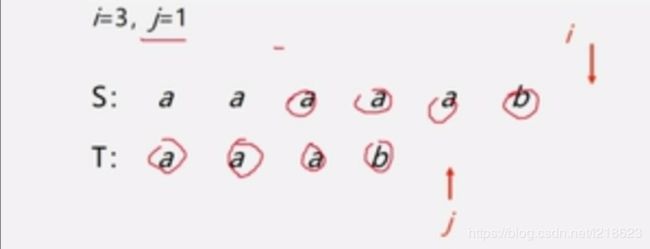
重复以上的比较过程:
直到这样,S 和 T 里都没有元素了,这样就匹配成功了,另外除了这种情况以外,还可能出现:
1 .S里还有元素,但是T里面已经没有元素了:
这样的话也是匹配成功了。
2 .S里面已经没有元素了,但是T里面还有元素没有匹配
这样的话是匹配不成功。
子串位置的计算:
就是像上图这样算的,用当前的 i 减去子串的长度,就得到子串的位置了。
过程呢就是这样:
那么我们用代码来实现一下:
由于我用了string,所以下标都是从0开始的,所以:
i 回溯时 回溯到 i-j+1的位置
j 回退时 回退到 0
匹配失败时返回 -1
#include
#include
using namespace std;
int Index_BF(string S,string T,int pos);//返回子串在主串中的位置
//pos表示从主串的第pos个位置开始查找子串
int main()
{
string S,T;//定义两个字符串
//赋值
S="aaaaab";
T="aaab";
//函数调用
int r=Index_BF(S,T,0);//表示从主串的第1个位置(下标为0的位置)开始查找子串
cout<<"子串的位置为:"<=T.size())//返回匹配成功的第一个字符的下标
{
return i-T.size();
}
else//匹配不成功
{
return -1;
}
}
运行结果:
可以看到输出结果为2,这代表子串在主串中的位置为主串下标为2的位置,所以就是第3个字符的位置了。
时间复杂度:
看不懂没关系,请看下面:
最好的情况下:
比较m次就够了,因为m是子串的长度,所以最少也需要把子串里的字符都匹配成功才行,所以时间复杂度为O(m)。
最坏情况下:
像上面那个图中的例子一样,每次都要比较到子串的最后一个字符1才发现匹配不成功(进行了4次匹配),直到最后(即主串中的后m位,即后4位)才匹配成功,所以除了后m(4)位以外,主串中前面的字符(n-m个字符)都要一一和子串进行m(4)次匹配,然后发现匹配不成功,所以就是(n-m)*m,再去加上最后m(4)个字符进行m(4)次匹配才发现匹配成功,所以就是(n-m)*m+m,即(n-m+1)*m。
(n-m+1)*m:(由于子串长度不可能大于主串的长度,所以存在以下两种情况)
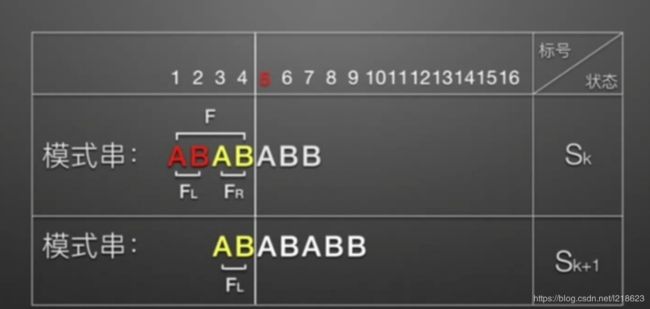
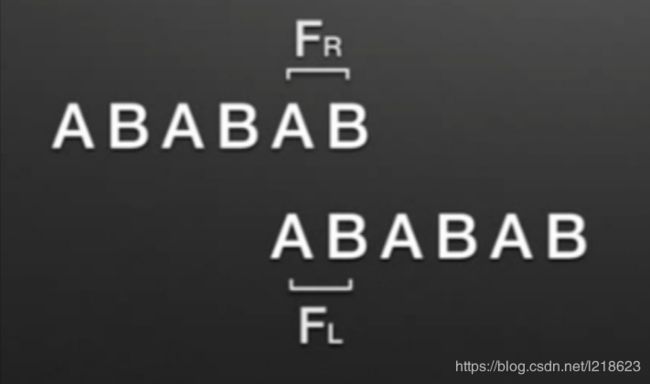
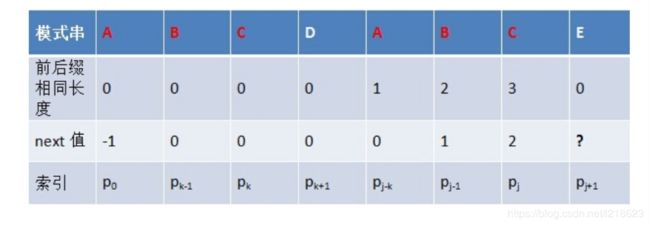
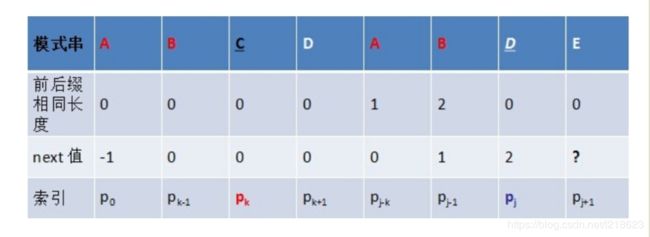
1. 当m< m和1都可以省略,即为n*m,所以时间复杂度为O(n*m)。 2.当m和n差不多大时: 可以近似等于(n+n+!)*m,即可以近似等于(2n)*m,所以时间复杂度还是O(n*m)。 平均情况下(有最好也有最坏): (m(最好情况下)+(n*m)(最坏情况下))/2=( (n+1)/2 )*m,所以数量级还为(n*m),所以时间复杂度为O(n*m)。 由于BF算法太慢,所以有了KMP算法。 KMP算法是D.E.Knuth、J.H.Morris和V.R.Pratt共同提出的,该算法较BF算法有较大的改进,从而使算法效率有了某种程度的提高。 它的提高方法:主串S的指针i不必回溯,可提速到O(n+m)(时间复杂度)。 先用图来理解一下: 这是用BF算法查找的过程,由这四步我们可以得到: 有这个对比我们可以看出,其实它的 i 的位置是没有变的,都是5,只是 j 的位置变了,而且j也没有重新回到1的位置,只是由5变到了3,因为前两个(AB)是匹配的,这就是KMP算法,能将Sk直接变到Sk+1这一步,而无需像上面BF算法那样Sk再回溯进行四步才能到Sk+1,是不是快了很多,那么到底是怎么实现的呢。 这张图有可能看不懂,它想表达的意思就是: 主串:A B A B B B A A A B A B A B B A 子串:A B A B A B B 我们可以看到,当进行到第5个位置的时候发现不匹配了,那我们要想主串 i 的位置不动,只移动子串的 j 的位置的话,到底应该移到哪,这才是KMP算法的难点重点,我们先以这个为例: 不难发现,子串中前两个字符AB和后两个字符AB(有下划线的)相同,而后两个字符AB是与主串中第三和第四个位置的字符是匹配好了的,所以子串中前两个字符AB与主串中第三和第四个位置的字符(AB)是必定匹配的,由于我们是从主串的第5个位置继续进行匹配的(主串 i 的位置不动),所以我们为了在移动子串之后,与主串第5个位置对应的字符(在这里是子串中第三个字符,即字符A)之前的字符串是必须匹配的,所以当 j=3的时候,子串j=3之前的字符AB与主串中第三和第四个位置的字符(AB)正好匹配,那么问题来了,我们怎么知道与主串那个位置(在这里即第5个位置)对应的是子串中的第几个字符呢。 方法:(找该位置之前字符串最大相同的前缀后缀) 从子串中的那个加粗的A(子串中第5个字符)开始倒着往前找与子串前几个字符相同的字符串,即: 我们先倒着找找到第4个字符(B),看其与第一个位置字符(A)不相同,再继续找,找到第3,4个位置(AB)的字符,发现它与第1,2个位置(AB) 的字符是完全相同的,之所以这样找是因为:子串的前4个字符一定是匹配好了的,所以第3,4个位置的字符一定与主串第3,4个位置的字符一定匹配,而子串中第3,4个位置的字符(AB)又与其第1,2个位置(AB) 的字符完全相同,所以子串中第1,2个位置的字符(AB)也一定与主串第3,4个位置的字符匹配,那么移动过后,就可以直接从子串的第3个位置再开始进行比较就可以了(因为子串中前两个字符AB已经匹配过了,无需再进行比较),所以就找到了 j 的要移动位置为移动到子串中的3位置。 具体的就是这样一个过程: 就如这样,当FL=FR时,即找到了最大相同前后缀,最大前缀为FL,最大后缀为FR,那么就从最大前缀的后一个字符(第三个位置的字符A)开始与主串进行比较匹配。 另外还有一种情况: 若出现以上这种情况,就是一个字符串中有短的重复串也有长的重复串,即它相同的前后缀有长有短的,那么我们选长的,也就是我们上面所说的找最大相同的前后缀。 原因: 它的匹配移动过程是这样的: 可以看到先经过第一个过程,再到第二个过程,那么如果我们选了短的的话,我们就会跳过长的这种情况而直接到了下面这种情况,那么很有可能就会错过那种长字符串情况下字符串匹配成功的情况。 通过以上这些,我们应该也了解到了最最重要的就是找 j 应该移动的位置,我们用一个一维数组( next[j] )来存储它每次移动的位置。 意思就是说,就比如 主串:B C A C B A B 子串:A C B A B 主串与子串第一个字符就不匹配,那么按KMP算法的思路的话,要让主串的 i 不动,移动子串的 j ,那么我们就需要找一下next[j],由于 j=1,所以实际上是将 j 移动到next[1] 的位置,而计算next[1]需要找子串 j 之前的字符串的最大前后缀,我们发现j=1之前根本就没有字符,所以就也不存在最大前后缀了,所以我们让next[1]=0,所以 j=0,在后续的操作中,如果 j=0,我们就让i++,j++,即得 i=2,j=1,这时就让主串的第2个字符与子串的第1个字符继续进行比较了。 而主串的第2个字符(C)与子串的第1个字符(A)仍然不匹配,则又根据next[1]=0,让 i++,j++,得 i=3,j=1,这时又让主串的第3个字符与子串的第1个字符进行比较了。 如(求next): 例子: 我们可以发现一个规律:next[j]=重合的字符个数+1。 用next[j]的值推导next[j+1]的值,即由上一个next的值来推导下一个next的值: 上图要是不明白,那就来看下面:(上图是从下标为1开始的(当 t=0时,next[j+1]=1),而下面的例子都是从下标为0开始的(所以当 t=0时,next[j+1]=0))。所以如果你不懂上面这张图的话,就不要看了(直接看下面的例子),上面这张图仅供参考就行。 如果对于值k,已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1( j 之前的最大前后缀)。 《1》若Pk=Pj,则next[j+1]=next[j]+1=k+1; 通过这图,就很容易明白了。 本来 j 之前的最大前后缀是AB,所以next[j]=k,现在求next[j+1],就要找 j+1之前的最大前后缀,而我们发现当Pk=Pj时,其最大前后缀就找到了,为ABC,所以此时next[j+1]=k+1=next[j]+1。 《2》当Pk不等于Pj时,如果此时P[next[k]]==P[j],则next[j+1]=next[k]+1,否则继续递归前缀索引 k=next[k],而后重复此过程。 到这里很多人就不明白了,不过没关系,下面我们来慢慢消化: 由于Pj不等于Pk,即ABC(前缀)与ABD(后缀)是不相同的,所以不存在长度为3的相同前缀后缀,那么我们就需要找长度短点的相同前缀后缀,即用P[next[k]]与Pj进行匹配,如上图,next[k]=0(在k处next的值为0,然后发现P0(A)也不等于Pj(D),即没有找到相同的前缀后缀,所以next[j+1]=0,即相当于E对应的next 值为0。 也有P[next[k]]与Pj进行匹配时,next[k]不为0的情况,那就继续让P[next[ next[k] ]]与Pj进行匹配,一直这样循环下去,直到找到最大相同前后缀(下面的情况) 或者 遇到 P0(向上述情况那样) 时。 当然也有找到最大相同前后缀的情况: 由于Pj不等于Pk,即DABC(前缀)与DABD(后缀)是不相同的,所以不存在长度为4的相同前缀后缀,那么我们就需要找长度短点的相同前缀后缀,即用P[next[k]]与Pj进行匹配,如上图,next[k]=0(在k处next的值为0,然后发现P0=Pj,即都为字符D,所以其最大相同的前后缀就为next[k]+1=1,相当于E对应的next 值为1(即字符E之前的字符串“DABCDABD”中有长度为1的相同前缀和后缀)。 由一次一次的推导计算(只研究子串就可以了),得: 此时next=3, j 移动到子串第3个位置,i 位置不变。 此时next=1, j 移动到子串第1个位置,i 位置不变。 此时nex[1]=0,则让 j=0,然后 i++,j++,得i=6,j=1,即 i 移动到主串下一个位置,j 位置不变,还是1 。 此时nex[1]=0,则 j=0,然后 i++,j++,得i=7,j=1,即 i 移动到主串下一个位置,j 位置不变,还是1 。 此时匹配,i++,j++ 此时next=1, j 移动到子串第1个位置,i 位置不变。 最后匹配成功。 大体上就是这样: 也就是: 1.当存在最大前后缀时,next[j]=k。 2.next[1]=0。 3.当不存在最大前后缀,j 也不等于1时(就是前两种情况都不满足时),next[j]=1。 由于我用了string,所以下标都是从0开始的,所以: next[0]= -1 j 回退时 回退到 next[j] 匹配失败时返回 -1 也可以这样写(实际上是一样的): 运行结果都是: 可以看到输出结果为2,这代表子串在主串中的位置为主串下标为2的位置,所以就是第3个字符的位置了。 子串:A B A B next:0 1 1 2 我们很容易发现一个问题: 假如说第四个 B 与主串失配了,那我们肯定是找next,next=2,然后移到第二个位置,发现又失配了,原因是第二个字符与第四个字符相同,所以失配是必然会发生的。 原因就在这: 当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]进行匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j ]]。 也就是说,当p[j] = p[ next[j ]],我们就需要直接跳过这次比较,让p[next[ next[j] ]]直接与p[j]进行比较。所以我们就需要在代码中加一个判断条件:p[j]是否等于p[next[j]]。 由于我用了string,所以下标都是从0开始的,所以: next[0]= -1 j 回退时 回退到 next[j] 匹配失败时返回 -1 运行结果: 可以看到输出结果为2,这代表子串在主串中的位置为主串下标为2的位置,所以就是第3个字符的位置了。 无论如何,都一定要有耐心认真的去看,这样才能看懂哦。 KMP算法
求解next的方法:
求next[j+1]:
那么我们使用next数组来实现一下这个过程:
代码:
#include#includenext 数组的优化:
代码:
#include